摘 要: 本论文通过前期效用理论在彩票中的应用, 说明了通常在预期效用最大化的缺陷, 解释了人们为什么也会背离EMU预测。
关键词: EMU; 预期效用; 前期效用;
预期效用假说是现代消费理论的一个分支。主要用于分析个人的风险决策行为, 它为个体决策者定义一个效用函数, 然后认为个体的决策会使自己的效用最大化。预期效用假设, 以冯·诺伊曼一莫根施特恩效用函数为基础, 正是它决定了消费者的效用函数。EMU (预期效果用最大化, expected…maximization…of…utility) 中的公理看起来是合理的, 但是实际上人们的决策通常却背离了EMU的预测。心理学家…Tversky…和Kahneman (1981年) 提出了前景效用理论和架构效应来试着解释为什么人们会背离EMU预测。预期效用最大化的缺陷:前期效用理论在不确定性决策中应用。
这里有一个EMU不能解释的决策示例。请一个人在彩票1和彩票2之间进行选择。
彩票1:稳获30元
彩票2: 80%的机会获得45元, 20%的机会获得0元
大多数人喜欢彩票1, 而不喜欢彩票2。接下来, 请同一个人在彩票3和彩票4之间进行选择。
彩票3:20%的机会获得45元, 80%的机会获得0元
彩票4:25%的机会获得30元, 75%的机会获得0元

大多数人会选择彩票3而不选择彩票4.现在, 让u (0) =0, u (45) =1.。当且仅当u (30) >0.8时, 遵守EMU的决策者将选择彩票1而不选择彩票2.当且仅当0.2>0.25u (30) 或u (30) <0.8时, 遵守EMU的决策者将选择彩票3而不选择彩票4.。这意味着相信EMU的人不选择彩票1而选择彩票2, 并且不选择彩票3, 而选择彩票4.因此, 对于这种情况, 大多数人的选择都与EMU相矛盾。Tversky和Kahneman提出了前景效用理论来解释我们刚刚所描述的决策制定矛盾。前景效用理论假设我们不把概率看做它们是在给定问题中。相反, 决策者可以把事件的概率p看做是“变形的”概率II (p) .看起来能够解释许多矛盾的II (p) 函数如图1所示。
图1……应用于效用函数的加权
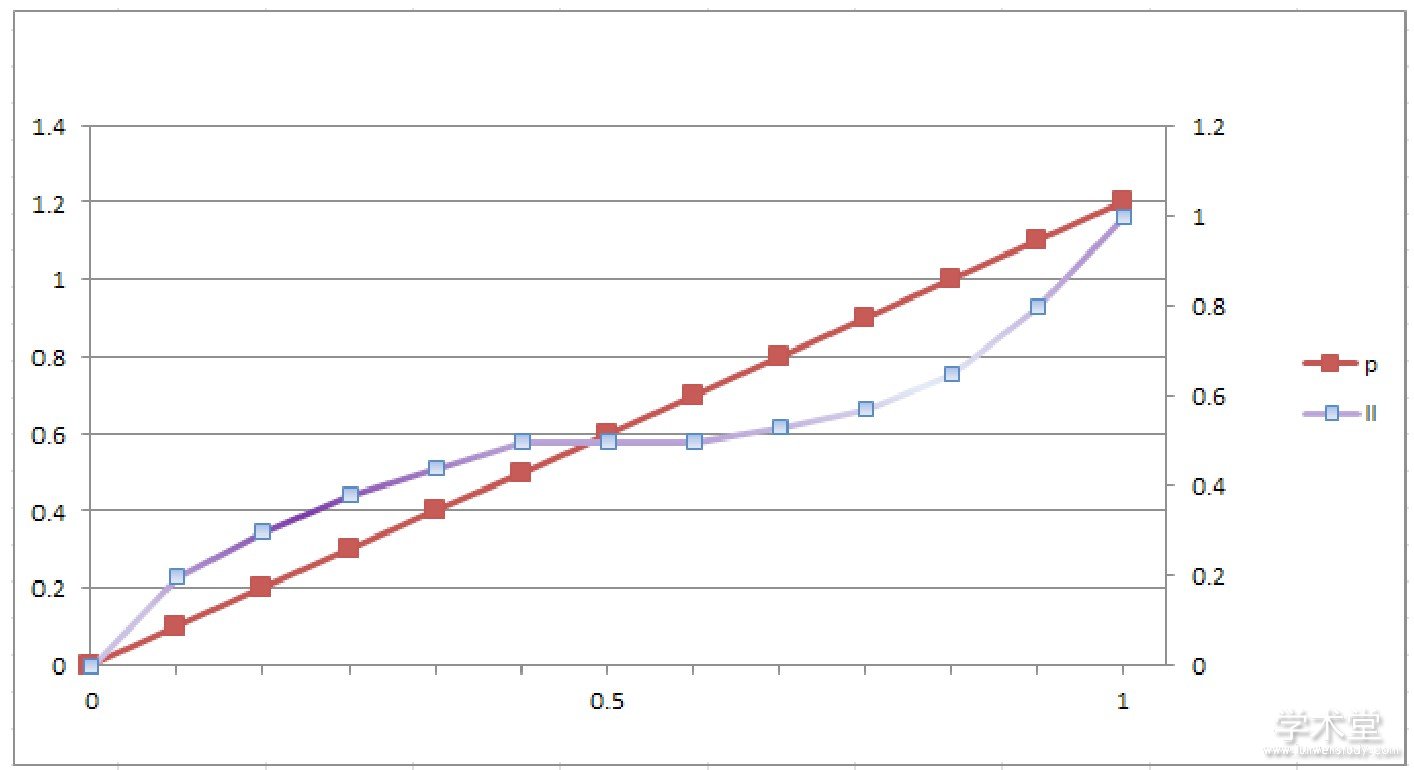
表1…彩票的前景效用
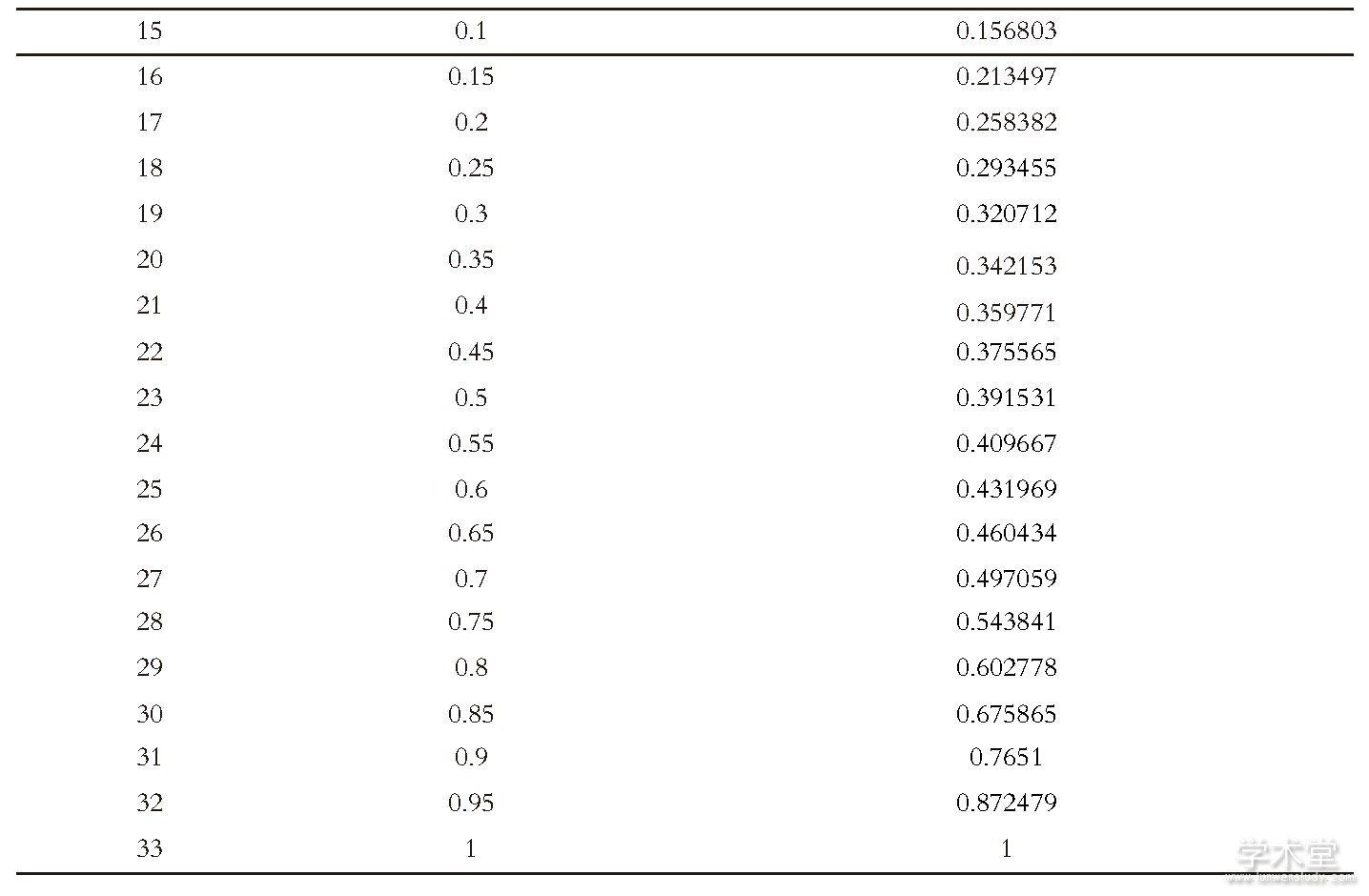
图中II (p) 函数的形状意味着当事件的概率较小 (接近于0) 或较大 (接近于1) 时, 人们对概率的变化较为敏感, 我们用于构造II (p) 曲线的方程是II (p) =1.89799p-3.55995p2+2.662549p2.前景效用理论如何解释我们的矛盾呢?根据图1-2中给定的II (p) 值, 我们可以比较彩票1相对于彩票2的预期“前景效用”和彩票3相对于彩票4的前景效用。
彩票1的前景效用:u (30)
彩票2的前景效用:0.602
彩票3的前景效用:0.258
彩票4的前景效用:0.293u (30)
因此, 如果u (30) >0.602, 则彩票1优于彩票2, 而如果0.258>0.293u (30) 或u (30) <0.258/0.293=0.88, 则彩票3优于彩票4。这时, 我们的矛盾就消失了, 因为对于大多数人而言, u (30) 将在0.602~0.88之间!
参考文献:
[1] 李伟民, 金融大辞典:[D].哈尔滨:黑龙江人民出版社, 2002:11.
[2]李保明, 刘家壮.效用函数与纳什均衡[D].山东:经济数学, 2000:24.
[3] 效用函数的概念.中国学网.2016-7-21[引用日期2016-12-12].