摘要:[目的]分析髋臼后柱顺行骨通道螺钉固定的生物力学特征。[方法] 64排螺旋CT扫描健康成年男性志愿者骨盆数据,建立志愿者骨盆三维有限元模型,设计出髋臼后柱几何骨通道螺钉钉道和两个任意钉道。测定未置入螺钉及置入螺钉时髋骨和螺钉的Von Mises应力与位移。[结果]有螺钉固定的骨盆皮质骨应力比正常骨盆稍大,使用几何螺钉时骨盆皮质骨应力最小,随着载荷的增大,各组模型皮质骨承受Von Mises应力均显着增加(P<0.05);无论骨盆是否有螺丝钉,骨小梁应力几乎相同,相同载荷下,正常髋骨受力应力最小,自由钉道2组螺钉受力最大,各组间差异有统计学意义(P<0.05);正常骨盆的位移明显大于螺钉固定的骨盆位移,各载荷条件下,几何钉道螺钉所承受应力最大(P<0.05),但几何钉道螺钉固定的骨盆位移最小(P<0.05)。随着载荷力的增大,各组螺钉所受应力逐渐加大(P<0.05)。[结论]几何钉道的螺钉发生应力集中大,但位移较小,是髋臼后柱骨折顺行骨通道螺钉置入的最优骨通道。
关键词:髋臼; 螺钉钉道; 应力分布; 有限元分析;
Finite element analysis on tracks of antegrade screw for fixation of acetabular posterior column
LI Ya-guang ZHANG Yuan-zhi SHI Zhi-qiang XU Zhi-gang LIU Gang MO Wei-peng
The Second Affiliated Hospital, Inner Mongolia Medical University The Affiliated Hospital, Inner Mongolia Medical University
Abstract:[Objective] To analyze the biomechanical characteristics of different tracks of anterograde screw placed for fixation of acetabular posterior column. [Method] The pelvic data of a healthy adult male volunteer who underwent 64-slice spiral CT scanning were processed to create three-dimensional finite element models. After that, anterograde screw placement in the geometric tract and other two tracts in arbitrary manner were mimicked on the models. Under different loadings, the Von Mises and displacement of the bone and screws were measured and compared among the intact bone model, the geometric tract model and other two models with arbitrary track. [Results]As increasing loading, the Von Mises stresses significantly increased on the acetabular bones in each model(P<0.05). Under the same loading, the intact model had the least stress, while the arbitrary track 2 model had the greatest stress with statistical significances among groups(P<0.05). Of the models with screw placements, the geometric model proved closed to the intact group mostly regarding the stress on the acetabular bones. In addition, the Von Mises stresses on the screw also significantly increased as the loads enhancing in the models with screw placement(P<0.05). Under the corresponding load, the geometric model had the greatest stress on the screw, whereas the least displacement of the screw among the 3 models with screw placement(P<0.05). [Conclusion] The geometric tract of antegrade screw placement might achieve the best fixation of acetabular posterior column with minimal stress concentration and displacement of the screw.
在全身所有骨折中,髋臼骨折的发病率约为3%,其中约13.4%的患者死亡[1]。髋臼骨折中最为常见的类型是累及髋臼后柱及后壁的骨折。临床多采用弧形钢板内固定的方法来稳定骨折,该方法固定可靠、骨折复位效果好,但亦存在切口大、暴露广、出血量多等问题。有学者建议采用螺钉来固定骨折,但在危险区域插入螺钉有穿透关节的风险。骨固定通道(osseous fixation pathways,OFPs)由Bishop等[2]首次提出,骨盆的骨性管结构复杂,但在几何上可视作为皮质骨圆柱体,具有不同的方向和尺寸,其内部空间可容纳骨内置入物,因此可通过螺钉置入的方法来治疗髋臼骨折,以此来使骨折的骨盆保持稳定。但是目前如何在术前规划阶段设计出既符满足生物力学上的要求又不损伤毗邻结构的最优的螺钉置入钉道,是临床开展运用中的关键。在以往的研究中,虽然通过对大量的标本进行了实验,但标本个体间较大的差异导致实验的数据过于庞大,加大了数据处理的难度。在这样的背景下,数字骨科技术成功地运用到髋臼后柱骨折的治疗中,使螺钉钉道的规划具备了新的手段。该技术运用计算机技术,结合医学影像与三维图像软件,对髋臼的解剖结构进行深度细致地分析,然后得到三维有限元骨盆实体模型,并对其可靠性与生物力学性能进行综合的分析。通过术前测量各种参数,在术前规划阶段对对手术过程进行模拟并得到螺钉置入的最优钉道,使螺钉固定更为牢靠,改善了手术的愈后。
1 资料与方法
1.1 研究对象
本研究选取了一名30岁男性志愿者作为研究对象,该男性既往体健,无骨骼畸形,无外伤史及手术史,无肿瘤史、结核病史等内外科病史。志愿者知情同意后并签订知情同意书,研究亦通过了内蒙古医科大学伦理委员会的审核。使用连续螺旋CT扫描腹部获得影像资料,研究所用的CT参数为电压:120k V,矩阵:512×512,层厚:0.625 mm。
1.2 模型建立
Materialise Mimics Innovation Suite 16.0软件(Materialise公司,比利时)导入原始Dicom格式数据,对骨盆进行三维重建,并以stl文件格式存储。在Solidwoks 2012软件中绘制出长度为120 mm,直径为7.3 mm的螺钉模型。运用Geomagic 2014软件对骨盆和螺钉模型进行光顺及去噪处理。将骨盆模型数据导入UGImageware 12.0软件中,以1.0 mm为间距运用自动分割结合部分人工干预的方法对髋臼后柱的骨结构进行多层剖分,并确定髋臼后柱安全区在每一层剖分面上的几何边界,提取几何边界点的二维图像坐标,然后拟合该边界的最大内切圆并获得其圆心坐标。最后利用最小二乘法拟合出一条距离各圆心点最近的空间直线,该直线即为拉力螺钉钉道的中轴线,其在几何上具备最优的性能,沿该中轴线即生成几何钉道(图1),记录钉道的位置、最大直径和长度。利用旋转、平移工具和配准方法,设计出两个位于安全区的自由钉道(任意钉道)。将髋骨和螺钉模型按照规划好的钉道进行装配,螺钉均沿设计钉道置入且未突破髋臼。
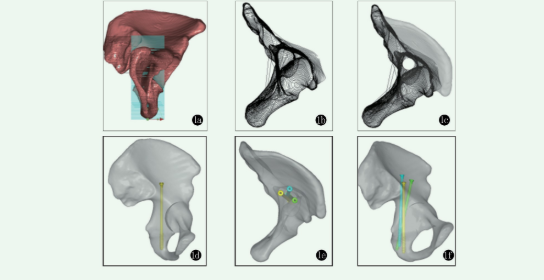
图1 髋臼后柱顺行螺钉固定几何钉道的确定1a:后柱分割1b:显示后柱通道1c:确定几何骨通道螺钉钉道1d:几何钉道骨通道螺钉固定1e,1f:几何钉道骨通道螺钉及任意钉道螺钉固定
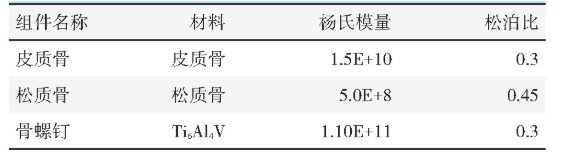
1.3 材料赋值与网格化
根据髋骨、股骨头和骨螺钉的不同材料属性分别对3种材料进行赋值,然后按不同的网格大小对各组件进行网格化处理(表1),具体是髋骨:1.0 mm,股骨头:1.0 mm,骨螺钉螺杆:0.5 mm,螺纹0.3 mm。
表1 材料属性
1.4 约束条件和加载
约束双侧骶髂关节耳状面作为边界条件,根据髋臼前倾角和外展角的解剖学定义,建立髋臼轴矢量,建立髋臼内面单元节点股骨头中心之间的约束单元[3]。沿上述矢量方向将压力载荷加载到耦合单元控制节点上,保证载荷均匀分布于髋臼内表面节点上。将数据导入ANSYS12.0软件,对其进行运算分析,用彩色等值线来表示不同的结果。
1.5 检测指标
将骨盆模型分别按“几何钉道”、两个自由钉道装配120 mm长度螺钉,分别施加600 N、1 200 N、2 400 N压力,重复10次,测量髋骨所受应力、髋骨的形变量、螺钉所受应力大小及螺钉形变量。
1.6 统计学方法
采用SPSS 19.0软件进行统计学分析,计量资料使用表示,组间比较采用单因素方差分析,组内比较采用配对t检验,P<0.05为差异有统计学意义。
2 结果
2.1 髋骨承受Von Mises应力与位移
表2、图2展示了各组的髋骨Von Mises应力与位移在施加3种载荷力时的变化情况,结果表明随载荷增大,各组髋骨承受Von Mises应力增加显着增加(P<0.05)。相同载荷下,正常髋骨所受应力最小,自由钉道1受力最大,各组间差异有统计学意义(P<0.05),其中,几何钉道组最接近正常髋骨。
表2 各组不同载荷下髋骨Von Mises应力与位移测量结果与比较
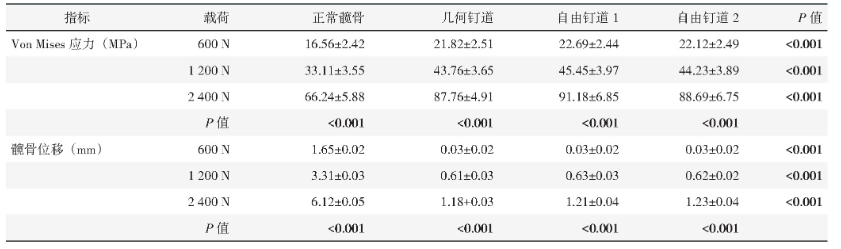
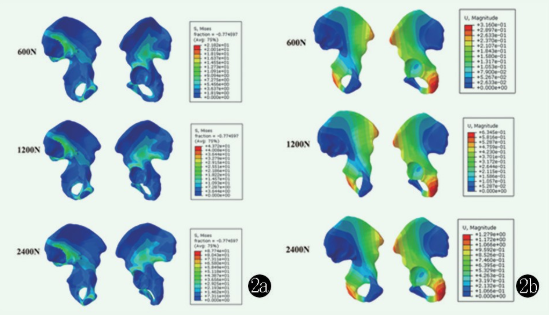
图2 不同载荷下髋骨Von Mises应力与位移测量2a:几何通道组髋骨Von Mises应力分布,随着加载力的增大,髋骨所受应力逐渐加大2b:几何通道组随加载力的增大,髋骨形变量逐渐加大
随载荷增大,正常组髋骨位移持续增大,而几何钉道组、自由钉道1组和自由钉道2组的固定骨盆位移差异无统计学意义(P>0.05)。
2.2 螺钉所受Von Mises应力及位移
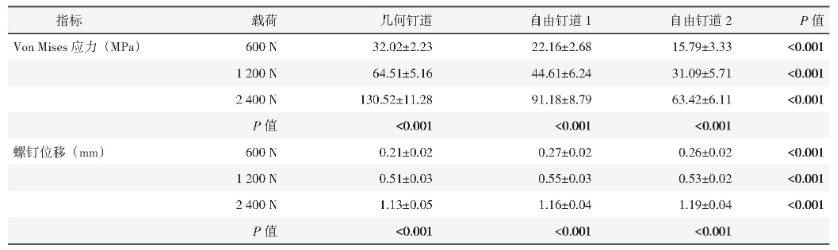
表3显示在分别加载600 N、1 200 N、2 400 N应力的情况下,各组螺钉承受的Von Mises应力与位移。随着载荷力的增大,各组螺钉所受应力逐渐加大(P<0.05);各载荷下,几何钉道螺钉承受应力最大(P<0.05)。随着载荷力的增大,螺钉位移逐渐加大(P<0.05);各载荷下,几何钉道组螺钉位移最小(P<0.05)。
表3 各组不同载荷下螺钉Von Mises应力与位移测量结果与比较
3 讨论
累及后柱及后壁的骨折频发于髋臼骨折中,其在髋臼骨折的发生率最高[4,5]。一般认为髋臼的危险区域位于坐骨棘中部[6,7],部分学者认为在此区域进行螺钉置入有加重损伤的风险,固定位置的偏差易使螺钉穿破骨盆壁或穿入关节内,导致邻近的神经血管以及脏器等重要组织结构的损伤[8]。其发生率在髋臼骨折手术的诸多术后并发症中最为显着[9,10]。
有大量研究探索了螺钉置入的问题,在进针角度上,Bosse[11]认为螺钉置入的方向应与患者的身体长轴冠状面平行,在后壁内侧部分的螺钉如能垂直置入于逆行髋臼表面则能得到稳定的骨折固定。Ebraheim等[12]对危险区边界进行了分析,通过研究尸体标本得出螺钉置入的安全角度为30°~49°的内侧角,并且后壁垂直于关节外。在进针点上,李洪恩等[13]提出可为骶髂关节前缘与髂前上棘连线的内、中1/3交界点,进针后螺钉沿着坐骨结节的中心点的方向置入。Mu等[14]认为选择顺行拉力螺钉的最佳进钉点时,应先找出距离骶髂关节前缘约(23.5±3.4) mm并位于弓状缘的点,经该点向髂骨内板作垂直线,据该点约(16.8±2.1) mm的点便是进针点,进钉时方向与矢状面成(57°36'±4°28')夹角,与冠状轴成(119°18'±2°32')夹角。王庆贤等[15]把髂前下棘的基底最前缘和骶髂关节作为参考,分别设为A点和B点,最佳进钉点便位于AB连线中的中垂线上,进针的方向为:与AB线呈(89.5°±3.20)°,与髂骨翼内侧呈(24.10°±1.7)°。Tadros等[16]发现髋臼后倾角(髋臼后柱两面切线的夹角)即安全角度存在个体差异,实验分析了231例髋臼后柱骨折患者(年龄15~74岁)的CT影像资料,得出其平均角度为39°(30°~47°),故通过术前对螺钉钉道的规划,可以使手术过程的安全性大大提升。
顺行拉力螺钉能较好的稳定髋臼后部的骨折,目前有大量实验着重于置钉的精准性的提升,譬如对于探索固定进钉导向装置和导航模板在骨折治疗中的可行性,但因人体骨盆存在差异性,这些研究均缺少个性化,且无关于生物力学的分析与验证[17,18]。通过影像技术可显示患者髋骨个体化的差异,那么能否借助影像数据针对性的规划出螺钉置入的最优通道?Ochs[19]分析了用逆行拉力螺钉固定髋臼后柱来实施微创治疗的可行性,所有操作在260例半骨盆三维模型上进行,实验额外考虑了性别因素的影响,同时详细测量了螺钉的长度、螺杆直径和角度,并对参考平面做出选择,研究结果表明男女的髋臼后柱钉道边界存在差异,且应将骨盆正中矢状平面和前后位作为参考平面,故在术前对钉道进行分析具有重要的意义。目前,多数学者认为臼顶负重区的复位是髋臼骨折治疗的重点,良好的复位能显着的改善预后。骨盆模型有着复杂的结构和不规则的形状,对其载荷和力学性能的分析测量难度大。相较于其他测量方法,有限元分析通过对分析每个节点的应力、应变,显示其应力的大小及方向,因此能提供更多的信息量,使关节表面及骨质内部的压力的测量更为精准。髂骨、坐骨及耻骨维持着骨盆的环形结构,在Von Mises应力分布图中显示出较大的应力集中。本次实验选用7.3 mm直径的螺钉,并以正常髋骨作为骨盆标本,依照手术对钉道的要求,分别设计出三种固定方式,包括两个自由钉道、几何钉道,并模拟髋臼后柱手术的实际状况。在进行有限元分析时,为了使髋骨模型相似于人体站立时的状态,于髋骨上方施予载荷力,力的大小由600 N、1 200 N、2 400 N依次增加,观察分析髋骨所受应力和形变量、螺钉所受应力和形变量在无螺钉置入髋骨和有螺钉置入髋骨时的情况,结果显示无螺钉置入的正常髋骨所受应力稍低于螺钉置入后的髋骨,且髋骨所受应力及髋骨形变量与载荷力呈现明显的正相关。沿着几何算法所示钉道置入的螺钉优于另两种钉道置入的螺钉,虽然几何钉道的螺钉所受应力最大,但其位移量在所有螺钉中最小。
相较于其他类似的研究,本研究的优点在于:(1)通过扫描以及重建,本研究所采用的骨盆模型与实体接近,保证了较小的误差范围;(2)运用计算机辅助技术,使对髋骨上的应力和螺旋形变量、螺钉上的应力等参数分析更为直观,为设计螺钉最佳的骨通道提供了参考依据。但本研究亦存在不足:实验中所加载的有限元模型仅为骨性结构,未将软组织诸如韧带及肌肉等数据导入模型中,且仅在计算机中完成,对骨盆力学环境的真实性变化反映稍有不足。
参考文献
[1]Carmaek DB,Moed BR,Me Carroll K,et al.Accuracy of detecting screw penetration of the acetabulum with intraoperative fluoroscopy and computed tomography[J].J Bone Joint Surg Am,2001,83(9):1370-1375.
[2]Bishop JA,Routt ML Jr.Osseous fixation pathways in pelvic and acetabular fracture surgery:osteology,radiology,and clinical applications[J].J Trauma Acute Care Surg,2012,72(6):1502-1509.
[3]Phillips AT,Pankaj P,Howie CR,et a1.Finite element modeling of the pelvis:inclusion of muscular and ligamentous boundary conditions[J].Med Eng Phys,2007,29(7):739-748.
[4]Heeg M,Klasen HJ,Visser JD.Operative treatment for acetabular fractures[J].J Bone Joint Surg Br,1990,72(3):383-386.
[5]Goulet JA,Rouleau JP,Mason DJ,et al.Comminuted fractures of the posterior wall of the acetabulum.A biomechanical evaluation of fixation methods[J].J Bone Joint Surg Am,1994,76(10):1457-1463.
[6]Matta JM,Letournel E,Browner BD.Surgical management of acetabular fractures[J].Instr Course Lect,1986,35 (2):382-397.
[7]Shahulhameed A,Roberts CS,Pomeroy CL,et al.Mapping the columns of the acetabulum--implications for percutaneous fixation[J].Injury,2010,41(4):339-342.
[8]Mast J,Jakob R,Ganz R.Planning and reduction technique in fracture surgery[M].Berlin:Heidelberg New York,Springer,1989.
[9]Letoumel E,Judet R.Fractures of the acetabulum[M].SpringerVerlag,Berlin Germany,1993:359-386.
[10]Letournel E.Acetabulum fractures:classification and management[J].Clin Orthop,1980,151 (1):81-106.
[11]Bosse MJ.Posterior acetabular wall fractures:a technique for screw placement[J].J Orthop Trauma,1991,5(2):167-172.
[12]Ebraheim NA,Waldrop J,Yeasting RA,et al.Danger zone of the acetabulum[J].J Orthop Trauma,1992,6(2):146-151.
[13]李洪恩,丛杰,李学举,等.穿裂性髋臼骨折的内固定治疗[J].中国矫形外科杂志,1999,6(5):333-336.
[14]Mu WD,Wang XQ,Jia TH,et a1.Quantitative anatomic basis of antegrade lag SCre W placement in posterior column of acetabulum[J].Arch Orthop Trauma Surg,2009,129(11):1531-1537.
[15]王庆贤,张英泽,潘进社,等.髋臼横断骨折不同内固定方式的生物力学研究[J].中华物理医学与康复杂志,2001,23 (5):279-281.
[16]Tadros AM,Oxland TR,O'Brien P.The retroacetabular angle determines the safe angle for screw placement in posterior acetabular fracture fixation[J].ISRN Orthop,2013,28:432675.
[17]张丕军,洪顾麒,陈凯宁,等.髋臼后柱骨折逆行拉力螺钉固定导向装置研制及初步验证[J].中华创伤杂志,2014,30(3):204-210.
[18]陈鸿奋,赵辉,王富明,等.髋臼后部骨折顺行拉力螺钉固定进钉导航模板的可行性研究[J].中华骨科杂志,2013,33(5):514-519.
[19]Ochs BG,Stuby FM,Stoeckle U,et al.Virtual mapping of 260three-dimensional hemipelvises to analyse gender-specific differences in minimally invasive retrograde lag screw placement in the posterior acetabular column using the anterior pelvic and midsagittal plane as reference[J].BMC Musculoskelet Disord,2015,16(2):240.