摘要:线性方程组有其明显的几何意义,以三元一次线性方程组为例,从理论上讨论了线性方程组解的几何意义与解的判定条件之间的联系,并据此,给出了一种简便判定线性方程组解的情况的一种方法。
关键词:线性方程组; 几何意义; 秩;
Abstract:There is significant geometrical significance of system of linear equations. Through taking the system of three linear equations as an example,the research discusses the relationship between geometrical significance of the solution of linear equation system and the solution of judging criteria theoretically. Based on this,the research proposes a simple method of judging the solution of linear equation system.
Keyword:Linear equation system; Geometrical significance; Rank;
0 引言
线性方程组是线性代数课程中一个重要内容,它在实际应用中有着重要作用,例如,稳态电路中的核心方程基尔霍夫方程、计算信号流图传递函数公式、网络流等,它们本质上是解线性方程组。解线性方程组都是基于重要的理论---线性方程组解的结构定理。三元一次线性方程组有着明显的几何背景,现大部分文献资料都是直接描述其解的几何含义,但未证明线性方程组解的几何含义与其解的判定条件之间的理论联系。本研究借助MATLAB软件直观展示线性方程组解的几何意义,从理论上证明线性方程组解的几何含义与解的判定条件之间的联系。
1 预备知识
设三元一次线性方程组为
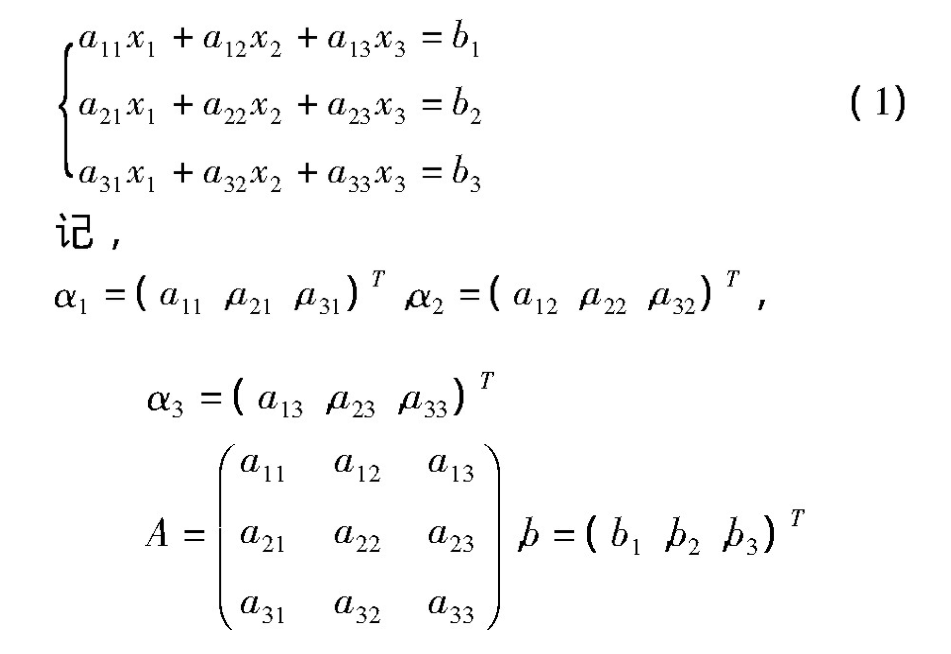
定义1 m×n矩阵A的所有非零子式的最高阶数称为矩阵A的秩。
引理1设两平面方程为
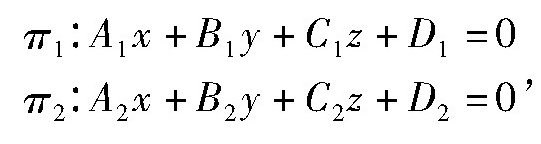
则
(i)两平面相交的充要条件是
A1:B1:C1≠A2:B2:C2;
(ii)两平面平行的充要条件是
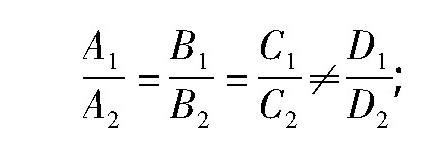
(iii)两平面重合的充要条件是
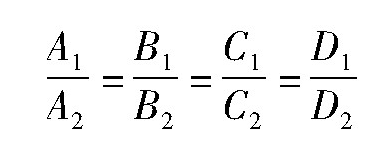
2 相关结论
线性方程组(1)的每一个方程表示三维空间中的一个平面,如果第二个方程与第一个方程联立,得到一个方程组,如有解,其解是维数小一维的直线,第三个方程也一样。这就生成两条新的直线,若这两条直线相交于一点,则方程组有唯一解。换句话说,三个平面相交于一点时,则线性方程组(1)有唯一解。下面借助于MATLAB,在二维平面中展示三元一次线性方程组解的其他情况。
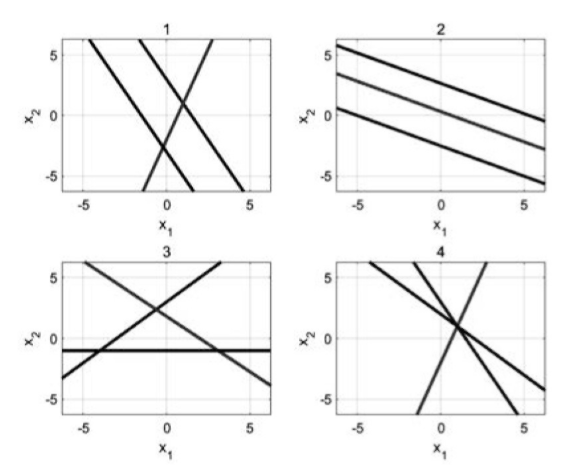
图1
注:每一条直线代表的是一个平面,每个交点代表的是一条直线。
由图1可知,1、3显示若两平面的交线在另一平面外,它们所对应的线性方程组无解;2显示无交线在第三个平面上,它所对应的线性方程组无解;4显示两平面的交线在第三个平面上,所对应的线性方程组有无穷多解。
从直线与平面位置关系研究线性方程组解的几何实验课含义与解的判定条件之间的联系。
设直线L方程为
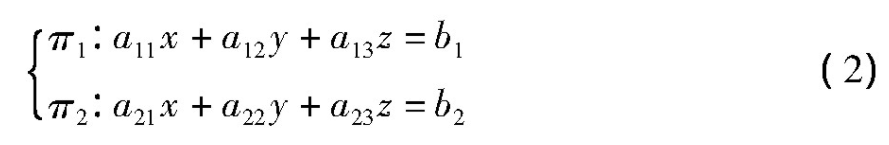
若a11:a12:a13≠a21:a22:a23,则直线(2)可以化为标准方程
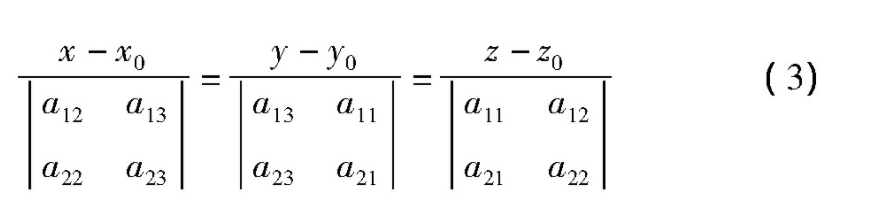
其中,
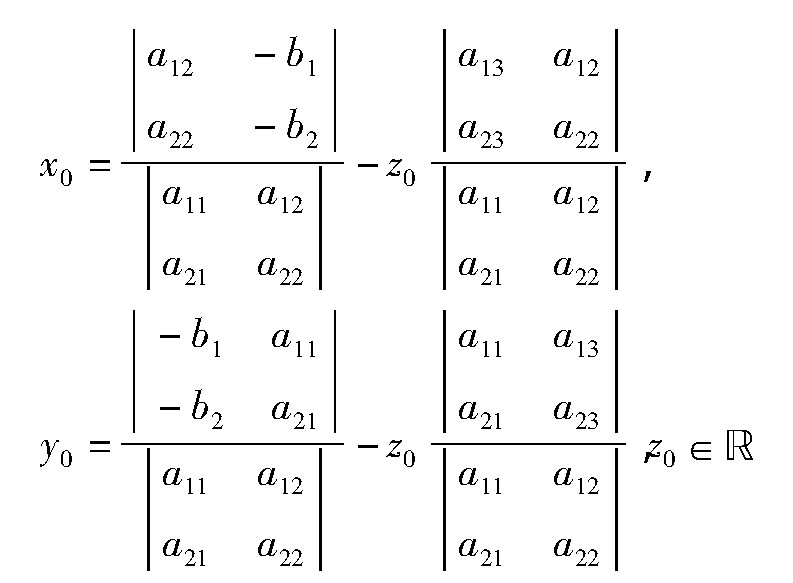
又设平面方程为
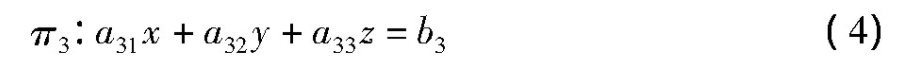
记
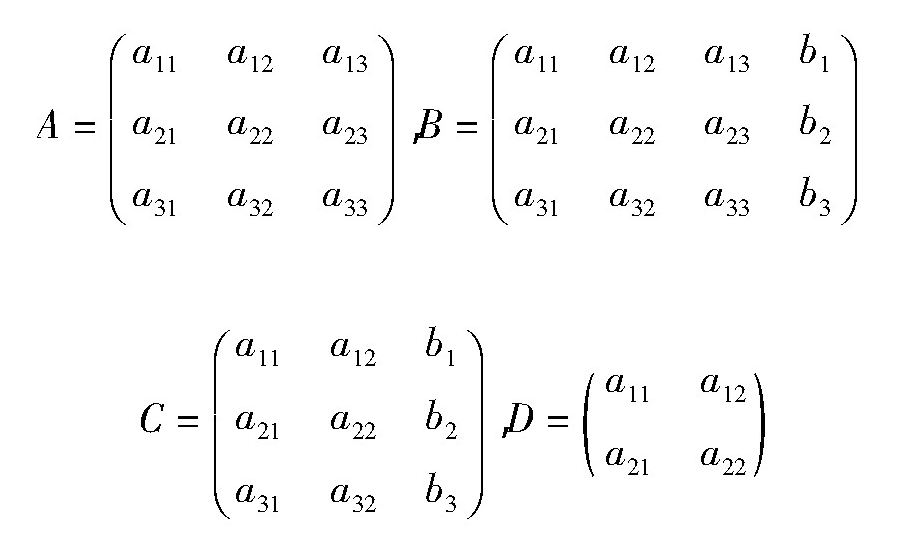
定理1直线(3)与平面(4)的相互位置关系有下面的充要条件:
(i)相交:r(A)=3;
(ii)平行:r(A)=2,r(B)=3;
(iii)直线在平面上:r(A)=r(B)=2
证明注意到,2≤r(A)≤3,令
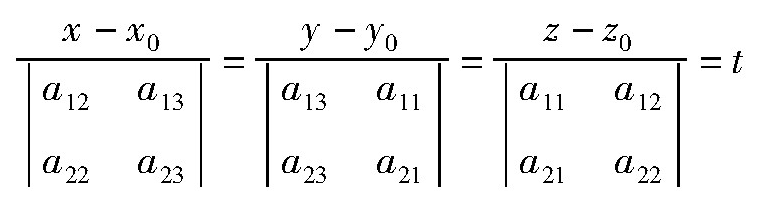
联立(4)化简得
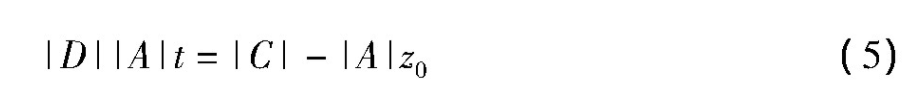
这是一个关于t的一元一次方程。
(i)若|A|≠0时,此时,方程(5)有唯一解,即直线与平面有唯一的交点。因此,当r(A)=3时,直线与平面相交;
(ii)若|A|=0,|C|≠0时,由于|C|≠0,则|B|有一个非零的三阶子式,即r(B)=3,此时方程(5)无解,即直线与平面无交点,也就是直线平行于平面。因此,当r(B)=3,r(A)=2时,直线与平面平行;
(iii)若|A|=0,|C|=0时,则α1,α2,α3线性相关,α1,α2,b也线性相关,则
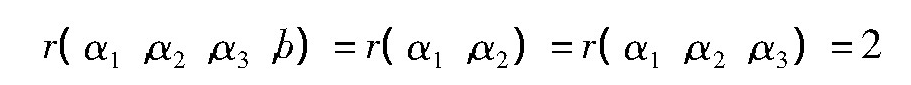
此时,方程(5)有无穷多解,即直线在平面上。因此,当r(A)=r(B)=2时,直线在平面上。
注:1.上面的证明过程是可逆的。2.根据上面的定理,从几何背景上判断线性方程组(1)解的情况只需看直线与平面的位置关系:当直线与平面相交时,线性方程组(1)有唯一解;当直线在平面外时,线性方程组(1)无解;当直线在平面上时,线性方程组(1)有无穷多解。
命题1三平面重合的充要条件是
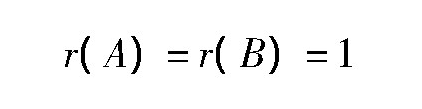
命题2三平面平行但不全重合的充要条件是
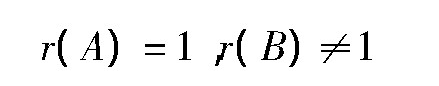
注:1.命题1、命题2可直接由引理1得到。2.命题1可以看成是无穷多条直线在平面上;命题2可以看成是无直线在平面上。
设三元一次线性方程组为
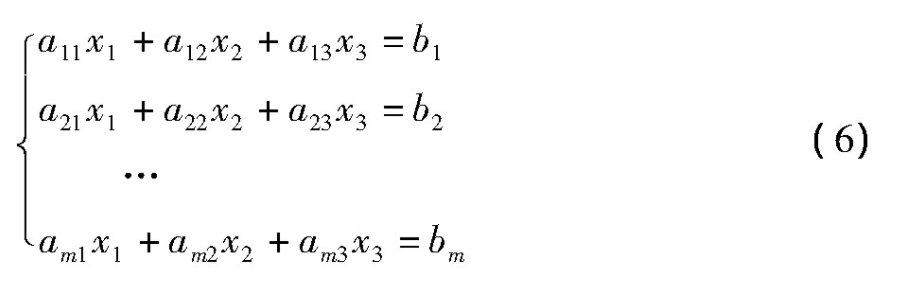
推论1 (i)线性方程组(6)有唯一解的充要条件是(6)中的m个方程所表示的平面相交于一点;
(ii)线性方程组(6)有无穷多解的充要条件是(6)中的m个方程所表示的m个平面重合或相交于一条直线;
(iii)线性方程组(6)无解,充要条件是(6)中的m个方程所表示m个平面既不相交于一点也不重合、相交于一条直线。
证明从线性方程组解的形式与直线、平面方程可得出结论,这里不再证明。
注:从定理1、命题1、命题2以及推论1的结论中也可以看出三元一次线性方程组解的结构形式:如果是平面重合,其解中含有两个自由变量,即其解的表达式实际上是一个平面方程;如果是平面相交于一条直线,其解中含有一个自由变量,即其解的表达式实际上是一条直线方程。
3 应用
例1设有三张不同的平面,其方程为aix+biy+ciz=di(i=1,2,3),它们组成的系数矩阵及增广矩阵的秩都为2,则三张平面可能的位置关系为()。(2002年数一)
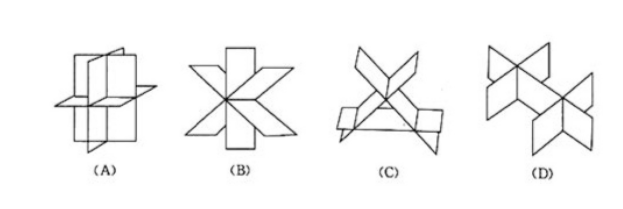
图2
解由于系数矩阵及增广矩阵的秩都为2,则方程组有无穷多解,根据定理1,应是两平面相交成的直线在第三个平面上,满足这个要求的只有B.
参考文献
[1] 吕林根,许子道。解析几何[M].北京:高等教育出版社,2009.
[2] Gilbert Strang.Introduction to Linear Algebra[M].Cambridge:Wellesley-Cambridge Press,2016.
[3]马金江,张凤然。用几何方法讨论线性方程组解的结构及其性质[J].高师理科学刊,2013,33(06):25-27.
[4]余丹,苑静。三元线性方程组的几何意义[J].科技信息,2009,(20):62.
[5]王金山,任蓓。齐次线性方程组存在全非零解的充要条件[J].大学数学,2005,21(02):95-97.