摘要:根据分数阶微积分的相关理论、Laplace变换、动力系统稳定性理论,研究了Rucklidge混沌系统的同步控制问题,给出了实现同步的同步方案,实现整数阶和分数阶Rucklidge系统的同步。结果表明:选取适当的控制律可以实现整数阶与分数阶混沌系统的主从同步。数值仿真表明了方案的可行性。
关键词:整数阶; 分数阶; Rucklidge系统; 混沌同步;
Abstract:According to the related theory of fractional calculus, Laplace transform and stability theory of dynamic system, the synchronization control problem of Rucklidge chaotic system is studied, and the synchronization scheme is given to realize the synchronization of integer-order and fractional-order Rucklidge systems. The results show that the integer-order and fractional-order Rucklidge systems can be realized by choosing appropriate control laws. Master-slave synchronization of chaotic systems. The numerical simulation shows the feasibility of the scheme.
Keyword:integer-order; fractional-order; Rucklidge systems; chaos synchronization;

0 引言
混沌同步一直是非线性科学研究的热点,由于分数阶系统更贴近系统模型本身,因而分数阶混沌系统的同步问题倍受关注[1,2].同步方式和方法多种多样,孙宁等[3]研究了一类不确定分数阶系统的滑模投影同步问题,实现了主从系统的投影同步。余明哲等[4]采用自适应滑模同步控制方法对一类分数阶不确定混沌系统同步控制问题加以探讨,能够使驱动-响应系统达到快速同步。仲启龙等[5]基于主动滑模控制方法实现了分数阶系统的混沌同步。张燕兰[6]研究了一类分数阶RayleighDuffling-like系统追踪投影广义同步问题。1992年Rucklidge在研究流体力学问题时提出了Rucklidge系统[7],谢红伟等[8]研究了一类Rucklidge混沌系统的自适应控制问题,而陈保颖等[9]对一类分数阶Rucklidge系统基于线性控制讨论了其同步问题。上述研究有的是整数阶系统与整数阶系统之间的同步,有的是分数阶与分数阶系统之间的同步。Hannachi[10]对分数阶与整数阶的三维连续系统的同步加以研究。在上述研究的基础上,本文研究了分数阶Rucklidge混沌系统与整数阶Rucklidge混沌系统的异结构同步问题,给出了系统取得同步的充分性条件,可以实现系统同步,最后给出数值仿真,仿真结果说明方法的有效性和可行性。
1 主要结果
定义1[11]Caputo分数阶导数定义为:
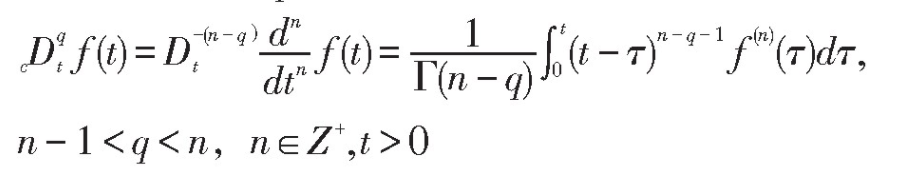
其中Γ(n)为伽马函数。
引理1 caputo分数阶导数的Laplace变换
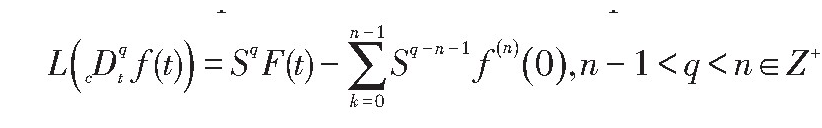
特别,当0<q≤1时
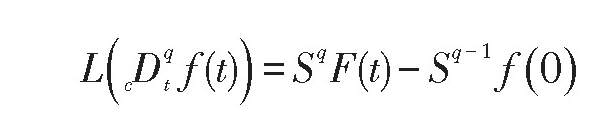
分数阶积分的Laplace变换
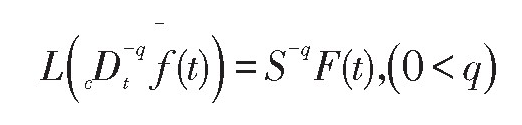
其中F(s)=L(f (t))。
考虑如下整数阶Rucklidge混沌系统[8],
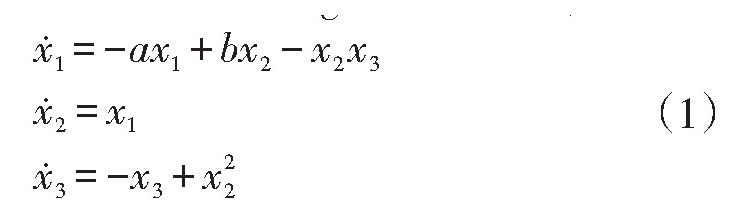
当a=2,b=6.7时系统呈现混沌态,如图1.
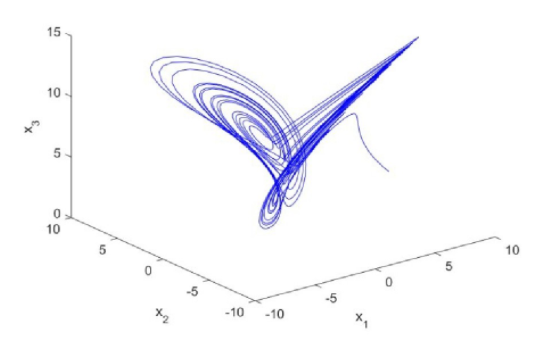
图1 整数阶系统的混沌吸引子
分数阶Rucklidge混沌系统[8]
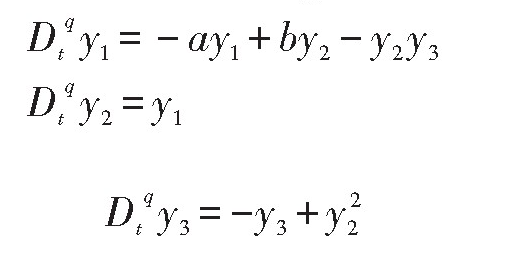
当a=2,b=6.7,q=0.978时系统呈现混沌态,如图2.
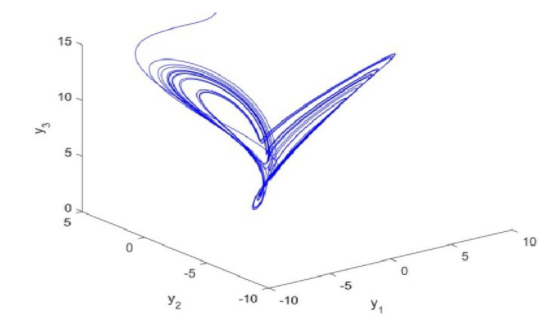
图2 分数阶系统的混沌吸引子
以系统(1)作为驱动系统,其对应的响应系统设计为
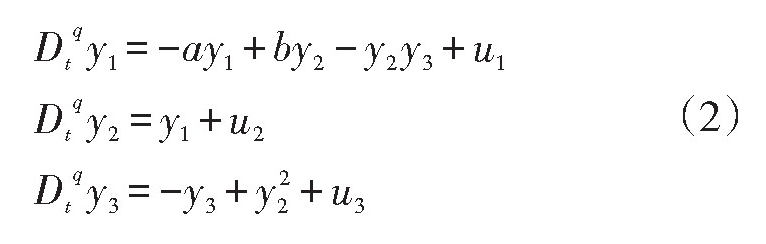
其中ui=ui1+ui2,(i=1,2,3)为控制器,取ui1:
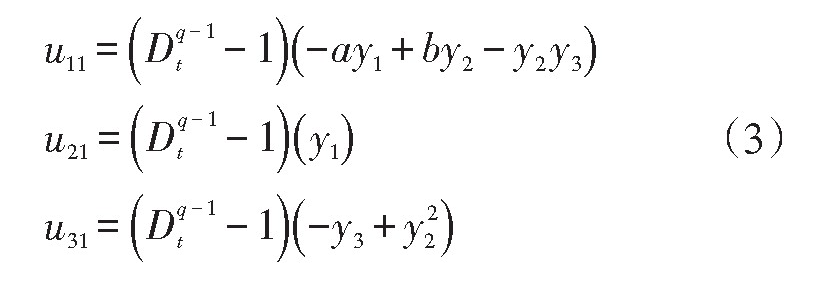
带入系统(2)为
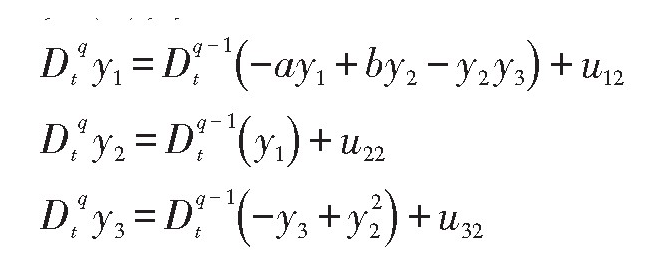
由引理1,对其做Laplace变换
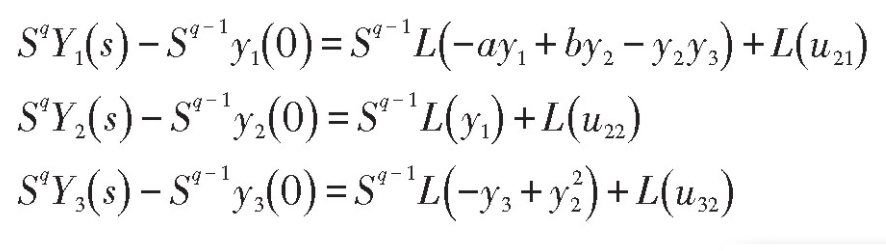
其中Yi(s)=L(yi(t)),两端乘以S1-q,再做La-place逆变换
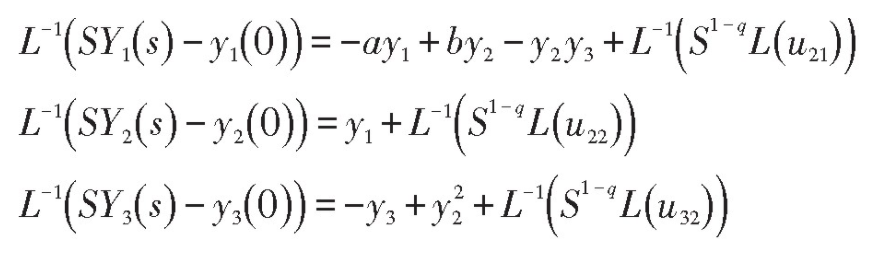
再由引理1
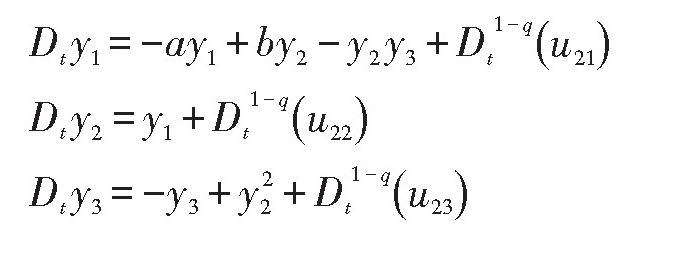
误差变量ei=yi-xi,(i=1,2,3),从而误差系统如下:
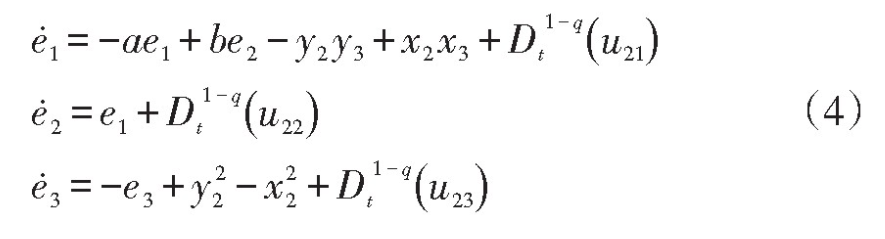
令
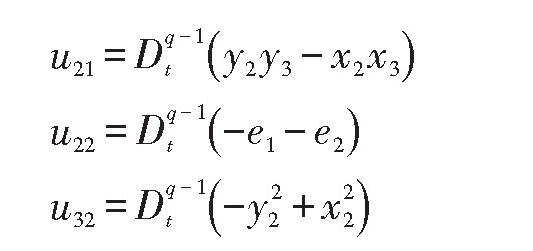
带入误差系统(4)有
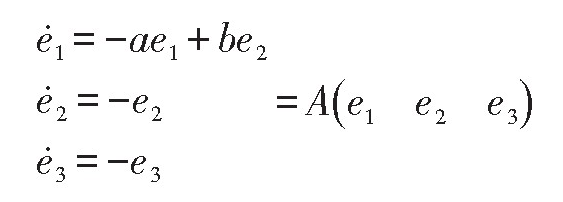
矩阵A为负定矩阵,由李雅普诺夫稳定性理论可知,误差系统(4)在原点处是渐进稳定的,从而系统(1)与系统(2)同步。
定理1在上述控制方案作用下,主从系统(1)与(2)是同步的。
从上述推导过程中可以看出,该控制方法非常灵活,控制器的第二部分可以任意构造,只要满足矩阵A为负定矩阵,满足李雅普诺夫稳定性理论的条件,可以保证误差系统在零点渐进稳定。当然,所构造控制器越简单,实现同步所用时间越短,控制方案也就越好。
2 数值仿真
以matlab为工具,分别在不加及加上控制器两种情形进行了数值仿真。系统中参数取值a=2,b=6.7,系统(2)中分数阶q=0.978;系统(1)状态变量初始值x(0)=(5,1,2),系统(2)状态变量初始值x(0)=(1,5,15)。从图3可以得知,在不加控制器的情况下,主从系统状态不趋一致,不同步;从图4得知,在加入控制器后主从系统状态很快趋近一致,实现同步;图5为系统误差曲线。
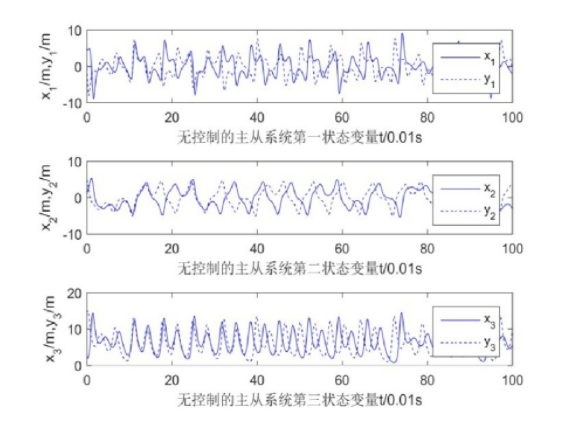
图3 无控制的主从系统状态
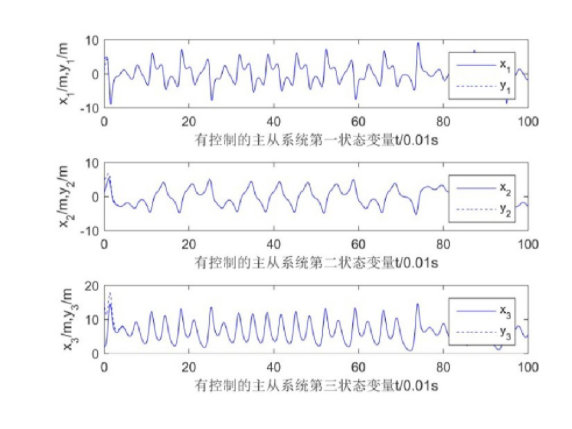
图4 有控制的主从系统状态
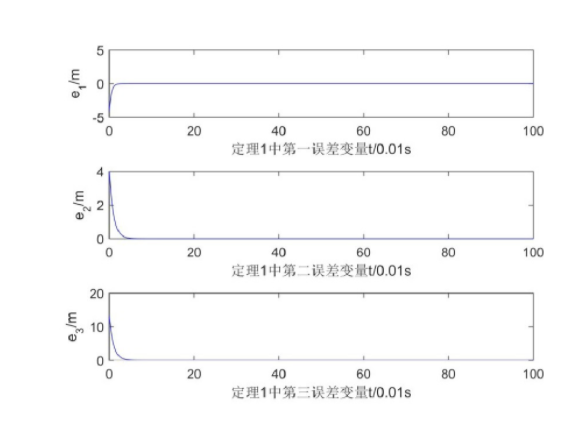
图5 定理1的系统误差曲线
3 结论
研究了Rucklidge混沌系统的同步控制问题,设计了控制方案,得到了整数阶分数阶Rucklidge混沌系统同步的充分性条件,给出了严格的数学证明和推理过程,仿真例子表明该方法有效。
参考文献
[1]毛北行,张玉霞。具有非线性耦合复杂网络混沌系统的有限时间同步[J].吉林大学学报(理学版),2015,53(4):757-761.
[2]陈烨,李生刚,刘恒。基于自适应模糊控制的分数阶混沌系统同步[J].物理学报,2016,65(17):501-511.
[3]孙宁,张化光,王智良。不确定分数阶混沌系统的滑模投影同步[J].浙江大学学报(工学版),2010,44(7):1288-1291.
[4]余明哲,张友安。一类不确定分数阶混沌系统的滑模自适应同步[J].北京航空航天大学学报,2014,40(9):1276-1280.
[5]仲启龙,邵永辉,郑永爱。分数阶混沌系统的主动滑模同步[J].动力学与控制学报,2015,13(1):18-22.
[6]张燕兰。分数阶Rayleigh-Duffling-like系统的自适应追踪广义投影同步[J].动力学与控制学报,2014,12(4):348-352.
[7]RUCKLIDGE A M.Chaos inmodels of doubleconvection[J].Fluid Mech,1992,237:209-229
[8]谢红伟,贾诺。Rucklidge混沌系统的自适应控制[J].哈尔滨师范大学学报(自然版),2015,31(6):16-18.
[9]陈保颖,张家军,苑占江。分数阶Rucklidge混沌系统的同步研究[J].动力学与控制学报,2010,8(3):234-238.
[10]HANNACHI F.A general robust method for the synchronization of fractional-integer-order 3-D continuous-time quadratic systems[J].International Journal of Dynamics and Control,2019,7(3):1084-1090.
[11]PODLUBNY.Fractional differential equation[M].Academic Press,New York,1999.