探讨凸函数在消费者效用最大化问题中的应用

　　0、凸函数的相关定义及引理

　　本文旨在通过对一些经济理论和现象的解释来揭示凸函数在微观经济学中的重要应用。先介绍凸函数相关理论以及微观经济学中的相关概念，并在此基础上探讨研究凸函数在微观经济学中的应用，再通过生产函数与效用函数等经济模型来展现凸函数在微观经济学中的应用，利用函数凹凸性探讨了凸函数相关理论在消费者效用最大化问题中的应用。

　　定义1:设f为定义在区间I上的函数，若对I上的任意两点x1,x2和任意实数λ∈(0,1)总有

　　反之，如果总有

　　如果（1）、（2）、（3）、（4）中的不等式改为严格不等式，则相应的函数称为严格凸函数和严格凹函数。

　　引理1:设f为区间I上的可导函数，则下述论断互相等价：（1）f为I上凸函数；（2）f′为I上的增函数；（3）对I上的任意两点x1，x2，有f(x)2≥f(x)1+f′(x)1(x)2-x1。

　　引理2:设f为区间I上的二阶可导函数，则在I上f为凸（凹）函数的充要条件是f″(x)≥0(f″(x)≤0),x∈I。显然,若-f为区间I上的凸函数，则f为区间I上的凹函数，所以我们只需讨论凸函数的性质即可。

　　1、凸函数在生产函数中的应用

　　定义3：经济学中的生产函数是指：在既定的工程技术知识水平下，给定投入之后所能够得到的最大的产出。简单来说，生产函数描述的就是在现有技术下，产品的最大产出量与所需要素投入量之间的关系。

　　生产函数通常可分为一种可变投入生产函数和多种可变投入生产函数。前者一般研究短期生产，而后者通常考察长期生产。生产函数Q可表示为：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　Q=f(L),K,N,E　　　　　　（5）

　　式中变量L表示产量，K表示投入劳动，N表示资本，E表示土地和企业家。一般情况下，我们将其简化为以下形式：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　Q=f(L),K　　　　　　　（6）

　　经济增长中所遇到的生产函数既有凸生产函数也有凹生产函数，这里要考察的是凸生产函数模型。

　　令总产量为TP=Q，平均产量为AP，边际产量（在其他投入保持不变的情况下，由于新增1单位的投入而多生产出来的产量或产出）为MP，假设Q=f(L),K是连续的。那么就有

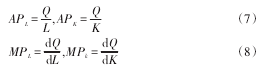
　　如果生产函数在某一区间上是凸函数，那么根据引理2在该区间上其二阶微分d2Q≥0，也就是说边际产量的微分dMP≥0。根据引理1知，可导凸函数的导函数是单调递增的，我们可以知道当生产函数为凸函数时，边际产量是递增的也就是说社会总产量的增长率是递增的。此时经济处于增长状态。相反，当生产函数为凹函数时，边际产量的微分dMP≤0，随着资本、劳动的投入总产量会减少。

　　于是，我们可以得出这样一个结论：在既定技术条件下，当生产函数为凸函数时经济处于增长状态，此时我们应当加大资本和劳动的投入以获取更大的产出。

　　2、凸函数在消费者效用最大化问题中的应用

　　下面我们来探讨凸函数在消费者效用最大化问题中的应用。在讨论消费者效用最大化问题之前，我们需要知道什么是效用。效用就是指消费者在消费时所感受到的满意度。

　　定义4：假设有n种商品，xi表示第i种商品的数量，消费者可以购买的商品组合为X=(x1,x2…xi…xn),它也被称为消费组合。令U表示满意度，那么效用函数就可以表示为U=U(x1,x2…xi…xn)。

　　对上述效用函数，我们也可以利用满意度大小对其赋值。对满意度较大的消费组合赋予较大的值，满意度较小的消费组合赋予较小的值，满意度相等的消费组合赋予相同的值。由于消费者对商品的满意度的值很难确定，所以在实际生活中，效用函数一般用来反映消费者对商品满意度的顺序。

　　消费者在实现效用最大化时还受到预算的约束。预算集是预算的集合，它表示在一定的消费者收入和商品价格的条件下，消费者可以买到商品的消费组合。令m表示消费者的收入，p=(p1,p2,…pn)为商品价格的集合，那么预算集就为：B(p,m)={x}∈X|xpT≤m所以消费者效用最大化问题就可以归结为在预算集中选择最优的消费组合,使得效用函数U(x)最大。也就是求：

　　定理2：效用函数U=U(x1,x2…xi…xn)必为严格凹函数。

　　证：消费者的消费行为就是消费者总是选择满意度最大的商品。对于商品a,b，令它们的效用函数为U(xa),U(xb)，不妨设消费者对商品a的满意度大于商品b，也就是U(xa)>U(xb)。假设存在商品c，使得商品c的效用函数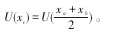

　　因为效用函数反映的是消费者对商品的满意度以及选择顺序，所以：

　　

　　因此，依据消费者的消费行为可以认定效用函数为严格凹函数。又因为预算集X(p,m)是非空的凸集，根据极值定理和凸函数的性质，可以推出最优解存在并且唯一。

　　定理3：当效用函数U=U(x1,x2…xi…xn)为严格凹函数，并且最优解存在时，最优解是唯一的。

　　证：设X1∈B(p),m为最优消费组合，也就是当消费组合为X1时，U(X1)最大。如果说最优消费组合不唯一，那么存在X2∈B(p),m，（X1≠X2）也使得U(X2)最大，并且U(X1)=U(X2)。因为预算集X(p,m)是非空的凸集，所以对于任意的α∈[0,1]都有

 

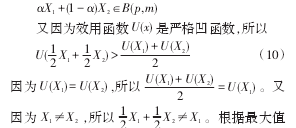
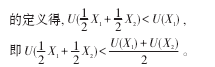
　　与不等式（10）矛盾。所以X1=X2，即最优消费组合是唯一的。

　　下面来举例说明当效用函数是严格凹函数时，最优的消费组合也即最优解的存在性。

　　例:消费者甲有现金400元，要去商贸城买某款衣服，一般每件在80元左右成交。她对该款衣服的满意度可用效用函数U(x)=-15x2+95x+10表示。x表示该款衣服的数量。根据数学模型（9）来求最优的消费组合。

　　根据预算集B(p,m)={x}∈X|xpT≤m我们可以等到不等式80x≤400，所以有x≤5。根据已知条件画图得：

　　

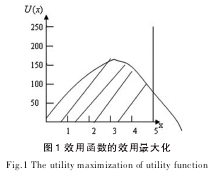
　　所以由图1可以看到，当效用函数取最大值时，所对应的消费组合就是最优解，也就是最优消费组合。所以求得当x=3.17时效用函数的值最大为160.42，因为x为整数，所以取x=3，此时效用为160。所以最优消费组合就是X={3}。

　　由上述例子我们可以看到：当效用函数为严格凹函数，在定义域内，它必然存在一个最大值。又因为当我们得到第一件商品时，此时对商品的满意程度必然是大于0，所以当x=1时，效用函数U(x)>0，它与x轴存在交点。所以在效用函数与x轴以及预算集所形成可行域内（如图1）必然存在一个最优解使得效用最大。

　　参考文献：
　　[1]（美）Jehle,G.A.,Reny,P.J.高级微观经济理论[M].上海:上海财经大学出版社,2002.
　　[2]（美）保罗·萨缪尔森,威廉·诺德豪斯.微观经济学[M].北京:人民邮电出版社,2008.
　　[3]邵宇.微观金融学及其数学基础[M].北京:清华大学出版社,2008.
　　[4]华东师范大学数学系.数学分析[M].北京:高等教育出版社,2001.
　　[5]严忠,刘之行,杨爱琴.高等数学[M].合肥:中国科学技术大学出版社,2010.
　　[6]陈宝林.最优化理论与算法(第2版)[M].北京：清华大学出版社,2005.
　　[7]潘劲松.函数凸性在微观经济学中的应用[J].中国西部科技,2011,10(36):13,40.