摘 要: 学业预警是加强学风建设、提高教学质量的一项举措, 课程绩点预测是其中一项必不可少的工作.在分析课程之间的关系基础上, 运用遗传优化BP神经网络算法对目标课程绩点进行预测.首先, 将百分制成绩转化为课程绩点;其次, 引入专业知识网络并建立课程社团;然后, 运用关联规则分析给出课程之间的关联性;接下来, 利用遗传算法优化BP神经网络, 提出预测课程绩点的算法;最后, 以本校数学专业成绩为分析数据, 讨论该预测方法的可行性和有效性.
关键词: 高校学生; 课程绩点; 预测方法;
Abstract: Academic performance pre-warning is an important method to strengthen the construction of academic style and improve the quality of teaching where the course grade prediction is absolutely necessary.Based on the analysis of the intercurricular relationships, the optimized BP neural network genetic algorithm is used to predict the course grade point.Firstly, through introducing the course grade point, the percentage system is converted into the course grade point.Secondly, aprofessional knowledge network is introduced and a course community is created.Then, those strong association between courses are presented by aid of the association rules.Fourthly, an algorithm to predict the course grade by means of genetic algorithm to optimize the BP neural network is put forth.Finally, the score data of mathematics major in our university is analyzed to illustrate the feasibility and effectiveness of our method.
Keyword: college students; course grade point; prediction method;
0、引言
随着国内高等教育从精英式教育走向大众化教育, 各个高校都在积极探索如何强化教学管理以加强学风建设和提高教学质量.2006年, 江西理工大学首创性提出学业预警制度, 并获得良好的效果和认同[1].学业预警是一种信息沟通和危机预测的制度, 它指的是教学管理部门依据学生管理办法和专业培养方案, 对学生学习情况进行统计调查, 将学习存在的问题以及所产生不良后果的信息及时告知学生和家长, 同时采取有效措施帮助学生顺利完成学业[1].
如何预测课程成绩并做到期初事前预警而不是期末事后处理, 这对教学管理工作来说具有较强的实用性和参考价值.然而, 在当前实际教学管理工作中, 学业预警更多的是使用初等统计方法分析学生所处的学习状态, 比如补考率、专业排名等.该方法虽然简单直观却不能做到期初预警.为此, 学者们开展了相关研究工作.王凯成[2]利用四种数据挖掘算法对学生课程绩点进行预测获知毕业时候的平均绩点, 王涛等[3]基于BP神经网络, 利用学生每学期的成绩作为模型输入, 以平均学分绩点作为模型输出, 给出平均学分绩点预测模型.注意到, 这两项工作都只对学业平均 (学分) 绩点做出预测, 而非具体课程成绩的预测.吴暾华[4]通过构造学业状态特征向量, 运用支持向量机得到非线性预测模型自动发现学习状态不佳的学生并做出预警, 陈勇[5]利用遗传优化神经网络构造成绩预测模型, 其研究具有较强的实用性, 朱东星[6]运用关联规则分析挖掘出学生课程考试成绩与毕业之间的关联关系, 为教务管理工作提供有价值的信息.

基于对相关文献的梳理, 运用数据挖掘算法对课程成绩进行预测并提出解决方案是当前学业预警的主流研究内容[2,3,4,5,6].上述已有研究基本以百分制成绩作为分析数据[5], 研究课程之间的关联性[6,7]、目标课程的成绩预测[5]、学生当前学习所处的状态[4]等.然而, 这些研究内容并未涉及到课程学分, 脱离了以学分制为主的评价体系.同时注意到, 每一个专业的培养方案和教学计划都具有整体性和系统性, 如果纯粹以学生成绩作为分析数据讨论课程的关联性而不考虑课程内容的相关性, 那么这样的课程关联性分析就缺乏合理性和科学性.这也是当前研究工作的一个不足之处.为此, 本文将对学生百分制成绩做一定预处理, 在综合考虑课程内容和课程成绩基础上研究讨论课程之间的关联性, 然后再运用合适的数据挖掘算法对课程成绩做一定预测, 从而为学业预警工作提供相关预测信息.
1、 课程绩点预测算法
1.1、 课程绩点的计算
为了加强学风建设、提高教学质量, 各个高校都在积极探索和采取有效措施改进学分制的教学管理体制.目前, 受到公认的成功经验是采取平均绩点制[8,9].平均绩点 (grade point average, GPA) , 是国际通行的学生学习质量综合评价指标.一般采用加权平均分的五级评分制计算GPA, 其计算公式为:
其中, GPi表示第i门课程绩点或简称绩点;Ci表示第i门课程学分.
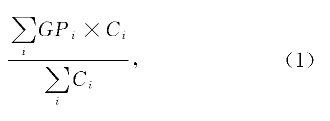
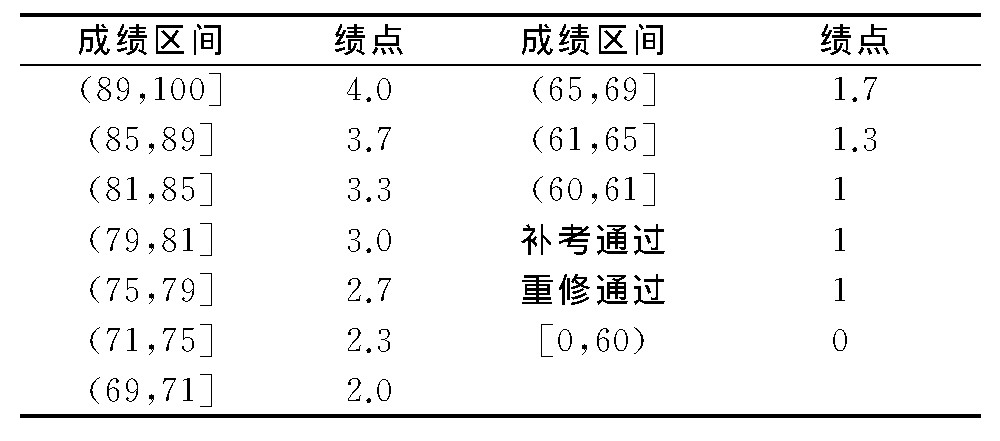
式 (1) 给出了GPA计算公式, 该指标可以用于评价学生学习状态以及是否达到毕业条件等[2,3].在该式中, 计算课程绩点GPi是其主要工作.课程绩点是根据每门课程的成绩来计算的, 一般将60分计为1个绩点, 往上每1分绩点增加0.1, 这样100分就是5个绩点.不过, 这样计算方法会使得课程绩点划分了太细, 反倒不利于后续讨论计算.因而, 采用成绩区间段来计算课程绩点是比较理想的方案, 比如武汉七所部属高校就是对不同成绩区间段给出不同的课程绩点[9].结合本校学生课程成绩以及学生综合测评的实际情况, 经过充分论证, 将采用表1的课程绩点计算规则.
表1 课程绩点计算规则
1.2 、专业知识网络和课程数据画像
为了分析课程之间的关联关系, 借鉴文献[10]的基本思想, 引入专业知识网络、课程数据画像等相关概念以及设计方法.这些将为后续分析作前期准备, 主要步骤如下:
(1) 先选取N门课程, 每门课程包含Nk, 1个知识单元、Nk, 2个知识点, k=1, 2, …, N;
(2) 分析课程知识点之间的联系, 用有向图G1=〈V1, E1〉来表示, 其中, 顶点集V1表示课程集, 有向边E1表示课程学习的先后顺序关系;
(3) 同样依据知识关联关系对知识单元和课程建立有向图, 分别记为G2=〈V2, E2〉、G3=〈V3, E3〉.同时, 将知识点提升为知识单元、知识单元归纳为课程.综合三个层次的专业知识有向图, 记为G=〈V, E〉;
(4) 用专业知识关联的数量计算出知识点 (vi, vj) 的关联程度wij, 并以此标记出图中每一条有向边的权重;
(5) 分析每个顶点的出入度din和dout、度分布特性、每个顶点vi与所有邻接节点 (〈vieijvj〉) 之间的实际连接与最大可能连接数之间的比率rij;
(6) 将整个网络进行划分, 形成几个具有共同特征的社团结构C (课程组) ;
(7) 建立专业知识有向图并做标识, 由此建立起课程数据画像.
1.3、 课程关联规则分析
在专业知识网络中, 课程社团是依据课程关联性结合在一起.在同一课程社团内, 课程之间就知识层面来说是相互关联的.然而, 这并不能作为课程关联规则分析之用, 也达不到预测的目的.为此, 在课程社团基础上, 运用关联规则分析算法计算出课程的强关联规则, 进而将规则中前置条件作为前导课程, 后置条件作为预测课程.具体方法如下.
首先, 假设C是一类课程社团, 令I={i1, i2, …, id}是该类课程社团中所有课程的集合, 共有d门课程.同时, 定义支持度和置信度以度量课程关联的强度, 公式如下:
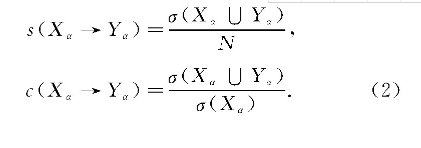
其中, N表示学生人数;σ (Xα∪Yα) 表示相对于绩点α来说在所有学生的课程事务中, 课程项集Xα和Yα所包含的所有课程绩点都大于α.
其次, 综合考虑所有课程绩点, 通过计算课程的总支持度和总置信度, 可以得到课程之间的强关联规则, 其计算公式如下:
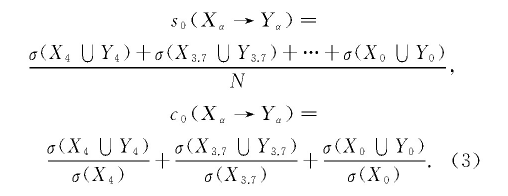
接下来, 运用Apriori算法, 可计算出在相对于绩点α下的课程之间的强关联规则.算法具体描述如下.
算法的输入部分
(1) 给定一类课程社团C和对应的课程集合I;
(2) 给定N个学生、绩点α和所有学生的课程事务的集合Tα;
(3) 给定一个最小支持度阈值a0和b0.
算法的输出部分
(1) 读取所有学生的课程事务, 产生待选的1-课程项集的集合C1;
(2) 参照最小支持度阈值, 通过待选的1-课程项集的集合C1产生频繁1-课程项集的集合L1;
(3) 取遍i>1, 循环执行下述步骤 (4-6) ;
(4) 通过Li执行连接和剪枝计算, 并且由待选的i+1-课程项集的集合Ci+1;
(5) 参照最小支持度阈值, 由待选的i+1-课程项集的集合Ci+1产生频繁i+1-课程项集的集合Li+1;
(6) 判断频繁Li是否为空集, 如果不为空集, 则令i=i+1并返回第 (4) 步, 否则执行第 (7) 步;
(7) 参照最小置信度, 返回频繁课程项集计算出强关联规则.
最后, 选取与预测课程相关的强关联规则, 按总支持度和总置信度大小排列取一定数量的关联课程 (前置条件) 作为预测的前导课程, 其后置条件作为预测课程.
1.4 、BP神经网络优化
运用遗传算法优化BP神经网络, 提出在强关联规则下的课程绩点预测算法.算法具体描述如下.
算法的输入部分
(1) 给定一类课程社团C和对应的课程集合I;
(2) 给定N个学生、绩点α和所有学生的课程事务的集合Tα;
(3) 给定一个最小支持度阈值a0和b0.
算法的输出部分
(1) 针对强关联规则的课程, 读取所有学生的课程绩点数据, 并对数据进行归一化等相关前期处理;
(2) 设置相关参数:节点数量、隐层数、次数、步长、目标等;
(3) 初始化种群的大小, 进化代数、交叉概率和 (初始) 变异概率等;
(4) 用十进制对种群进行编码, 取适应度函数为实际输出与期望输出绩点不相同的个数与总数之间的比值;
(5) 不断循环直至进化次数, 该过程进行交叉操作、变异操作、选择操作等自适应遗传操作以便产生新种群, 将得到最优个体作为BP神经网络的初始权值和阈值;
(6) 利用循环计算得到的最佳初始权值和阈值设置BP神经网络;
(7) 使用训练数据train训练BP神经网络;
(8) 使用测试数据input_test测试BP神经网络, 并将预测数据反归一化;
(9) 返回分析期望数据与预测数据之间的误差.
2 、实例分析
首先, 从教务系统获取数学专业2006~2016级633位学生课程成绩作为分析数据, 其中一部分作为训练数据, 另一部分作为验证数据.
其次, 对课程成绩数据做如下预处理: (1) 选修课因人而异不具有群体性, 故不列入分析讨论范围; (2) 确认正考成绩、补考成绩和重修成绩, 取最高分为最终成绩; (3) 计算每门课程的绩点.
然后, 在数据预处理基础上选取17门专业课程作为分析对象 (见表2) .运用Apriori算法对这些课程进行关联分析, 按支持度高低进行排列, 同时取前5门置信较度的课程作为关联课程, 相关结果见表2.在考虑开课时间顺序的基础上, 选取三组课程做绩点预测分析.课程组一:高等代数2、概率统计、运筹学、常微分方程和复变函数作为训练输入, 数学模型作为目标输出.课程组二:复变函数、数学分析3、概率统计、大学物理和常微分方程作为训练输入, 数值方法作为目标输出.课程组三:数据结构、数学分析1、高等代数2、程序设计和常微分方程作为训练输入, 数值方法作为目标输出.注意到课程组二和课程组三的目标输出课程都是数值方法, 不同的是:对于课程组二的训练输入课程, 仅通过绩点的关联性强度高低来选取;对于课程组三的训练输入课程, 不但要考虑绩点的关联性强度还要结合专业知识网络、所在课程社团以及知识之间关联程度.
表2 强关联课程和目标课程

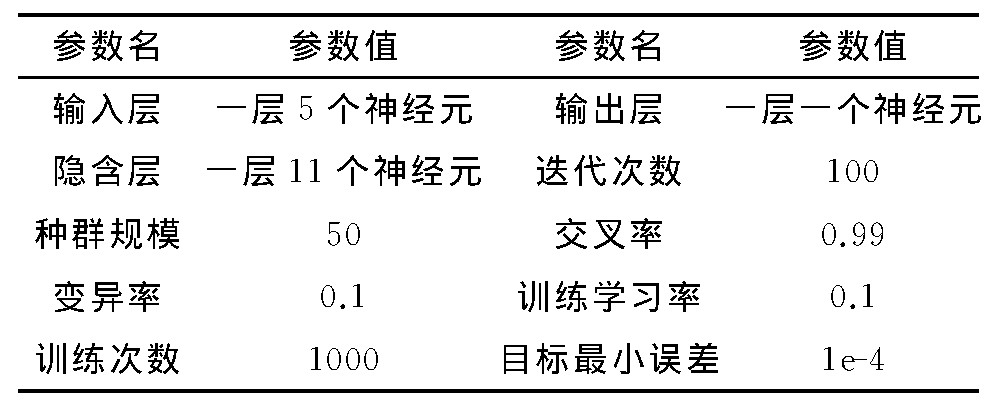
最后, 设定相关参数构建遗传优化BP神经网络算法.在神经网络中, 因为有5个关联课程和1个目标课程, 所以输入层和输出层的神经元 (节点数) 分别设定为5个和1个;隐含层的神经元个数设定为11个, 整体逼近效果较好.在遗传算法中, 经过不断实验调试给出较优的参数设定值, 见表3.
表3 遗传优化BP神经网络算法的参数设定
通过编程计算, 分别得到三个课程组的目标课程绩点的预测值和误差值 (见表4和图1~4) .具体分析如下:
第一, 表4和图1~4分别给出目标课程绩点的预测值和误差值, 结果表明该方法对预测目标课程绩点总体效果较为良好, 有84%以上学生的目标课程绩点的误差在1个数值范围内.
第二, 图2给出了课程组二和课题组三的目标课程绩点的误差对比图, 从图中可以看出课程组三的预测效果优于课题组二, 这说明结合专业知识网络、课程社团和知识之间关联程度对于提高课程绩点的预测准确度是很有必要的.同时, 从专业角度来看, 与课题组二对比, 课程组三的训练输入课程对目标输出课程有更强的课程内容相关性, 这使得预测结果更具有合理性和科学性.
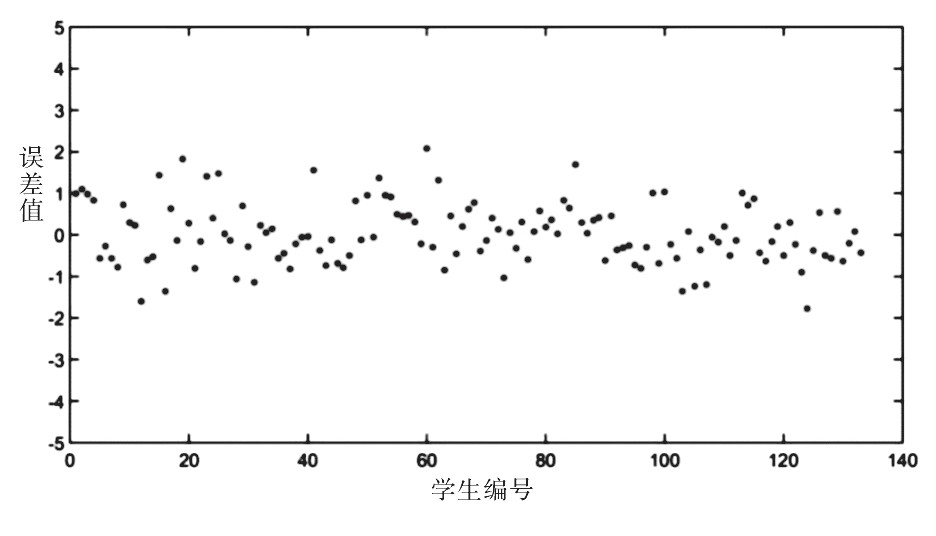
第三, 图3~4均给出课题组三的目标课程绩点的误差值, 其中图3涉及到预测学生数为83人, 图4涉及到预测学生数为133人.两个实验预测效果均为良好, 说明该方法对于预测数量来说具有很强的稳健性.
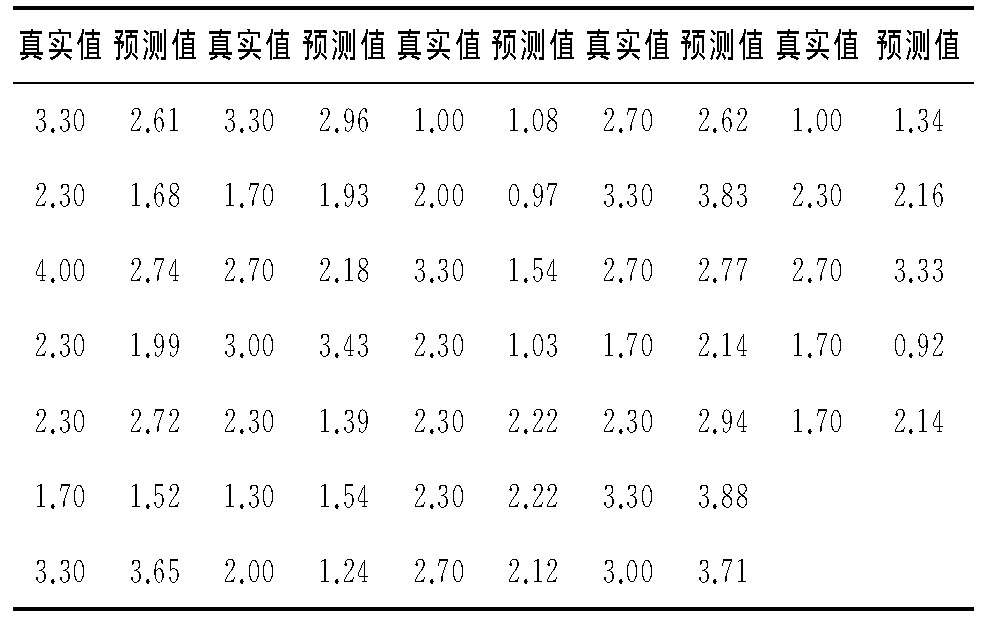
表4 课程组一的绩点真实值和预测值
3、 讨论
通过上述分析可以看出, 在对成绩数据做前期预处理和关联性分析基础上运用遗传优化BP神经网络算法对课程绩点进行预测具有如下特色和优势:
图1 课程组一的绩点误差
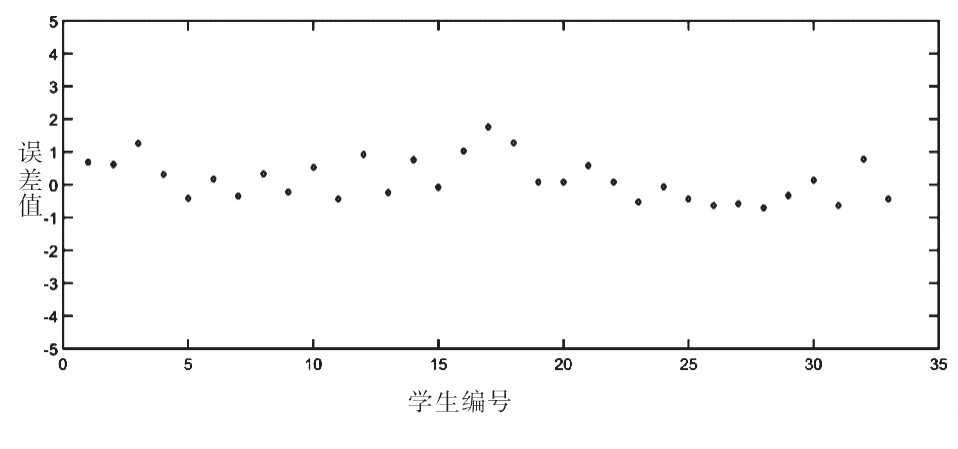
图2 课程组二、课程组三的绩点误差值的对比
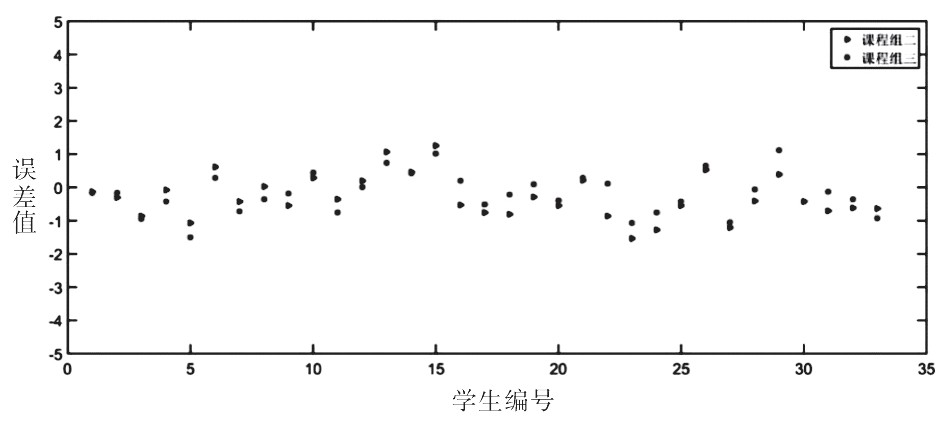
图3 课程组三的绩点误差 (83人)
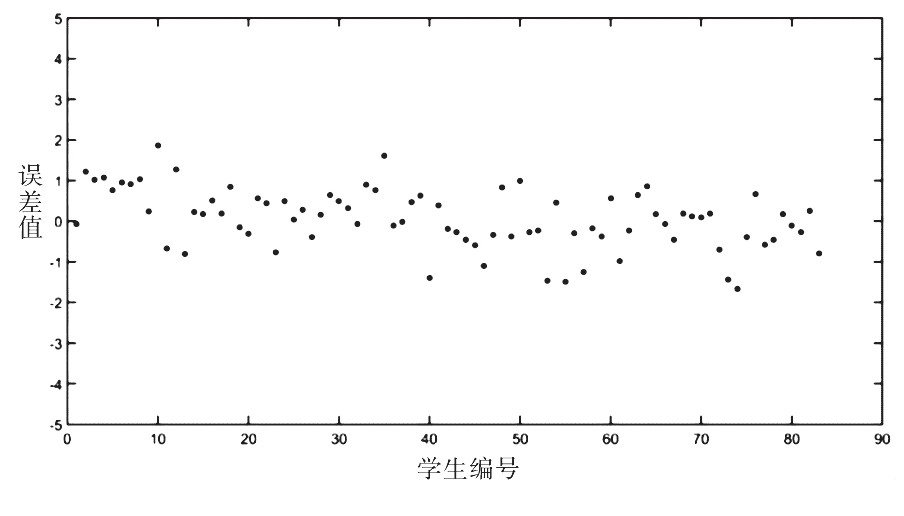
图4 课程组三的绩点误差 (133人)
第一, GPA作为学分制下评价学生成绩好坏的依据, 在教学管理上有较多的应用, 比如毕业资格审核、奖学金评选、学业预警等.根据计算公式GPA是通过课程绩点和对应课程学分计算出来的.因而, 分析和预测课程绩点对于GPA在教学管理中的应用特别是学业预警方面是必要的前期工作.注意到, 已有文献是以学生百分制成绩做学业预警分析[5], 而对课程绩点预测是这方面研究的一个补充.
第二, 区别于已有文献[6,7]对课程关联分析的研究方法, 在专业网络分析基础进行关联性分析的方法不但考虑了课程内容之间的关联性也考虑了以成绩为数据的课程之间关联性, 这样分析结果更加客观合理.
第三, 相关研究表明BP神经网络算法对课程成绩预测具有一定的不适应性, 表现在收敛速度慢、效率低下等[11].因而, 需要对该算法进行一定的优化.解决该问题的一种比较好方法是应用遗传算法优化BP神经网络, 它能够减少网络陷入局部极小的可能性, 同时也提高网络收敛的速度, 从而获得全局最优解[5,11].
4 、结论
本文主要以课程绩点为分析数据, 引入专业知识网络, 在强关联规则下利用遗传算法优化BP神经网络, 运用改进后的算法对课程绩点进行预测, 通过实例分析表明该解决方法对于课程绩点预测总体效果较为良好.
进一步将继续沿用GPA考核体系, 对所提出的预测方案予以优化以提高预测的准确度.同时作为结果的应用, 在教学改革重点项目支撑下, 正在研究开发专业知识网络和学业预警系统, 相关结果将在系统使用中得以体现.对于教学管理者来说, 可以根据前导关联课程的绩点, 对学生后续课程绩点进行预测, 并做好期初预警工作;对于学生来说, 在接收到相关课程预警之后, 可以通过对关联课程进行复习以及改变学习态度和学习方法, 以利于提高目标课程绩点.
参考文献
[1]吴婉淑.从学籍管理的角度谈高校学业预警[J].文教资料, 2014 (7) :115-117.
[2]王凯成.基于数据挖掘的大学生学业预警研究[D].上海:上海师范大学, 2012.
[3]王涛, 潘和平, 蔡成梅.基于L-M优化算法的学会绩点预测模型构建[J].合肥师范学院学报, 2017, 35 (6) :20-24.
[4]吴暾华, 王萍, 刘婷.基于支持向量机的大学生学业动态预警研究[J].中国教育信息化, 2017 (17) :65-67.
[5]陈勇.基于遗传神经网络成绩预测的研究与实现[J].现代电子技术, 2016, 39 (5) :96-100.
[6]朱东星, 沈良忠.关联规则在高校学业预警中的应用研究[J].电脑知识与技术, 2017, 13 (23) :196-197.
[7]何楚, 宋健, 卓桐.基于频繁模式谱聚类的课程关联分类模型和学生成绩预测算法研究[J].计算机应用研究, 2015, 32 (10) :2930-2932.
[8]杨亚河, 张双祥.平均绩点 (GPA) :学分制下的学习成绩评价标准和依据[J].吉林教育, 2012 (25) :32-33.
[9]方祥玉.学分绩点在武汉七所部属高校的实践与探索[J].河南教育学院学报 (哲学社会科学版) , 2012, 31 (3) :131-133.
[10]阎高伟, 张梦蓓, 程永强, 等.基于复杂网络的自动化专业知识体系分析[J].电气电子教学学报, 2016, 38 (4) :1-5.
[11]SOCHA K, BLUM C.An ant colony optimization algorithm for continuous optimization:application to feed-forward neural network training[J].Neural Computing and Applications, 2007, 16 (3) :235-247.