新的刀位优化算法和刀轨规划方法开发

　　０引言

    圆弧过渡曲面常用于组合曲面之间的光滑过渡连接，广泛出现在航空发动机机匣、涡轮叶片等关键零件的设计中。这类零件结构复杂、精度要求高、加工难度大，其加工程序的好坏直接关系到整机的加工质量和生产效率。传统中，对于圆弧过渡面的加工主要通过靠刀法［１，２］来实现，但频繁的换刀带来了成本高，工作效率低且质量不稳定等问题。因此，这种方法已逐渐被摒弃，转而采用在原有轨迹的基础上增补刀轨的方法，即采用行切算法进行刀具路径规划［３］，这种方法可去除全部残料，路径连续，抬刀少且效率高，但在加工时由于圆弧过渡面路径方向突变会经常发生崩齿现象。因此如何从根本上解决圆弧过渡面的质量控制仍是一个有待解决的问题。

　　近年来，利用具有复杂结构的环形刀具和鼓形刀具加工自由曲面得到极大的发展。文献［４］中利用圆环面刀进行组合曲面底部区域的清根加工，但该方法仍然没有克服切削力急剧增加的问题。文献［５］中应用定半径凹鼓形刀加工变曲率半径凸过渡曲面，通过调整刀具摆角实现变曲率圆弧的加工，但其定义的凹鼓形刀对于在横截面方向具有凹特性的圆角过渡面并不适用。

　　针对上述问题，本文的研究内容主要集中在两个方面：①设计一种具有复杂母线的环形刀具模型，利用母线上的不同部位加工零件曲面结构的不同部位，解决常规成型铣刀加工接触长度过大引起的切削力急剧增加问题；②开发出新的刀位优化算法和刀轨规划方法，在控制切削力的条件下有效提高加工效率。

　　１双圆弧锥形环形刀几何模型图

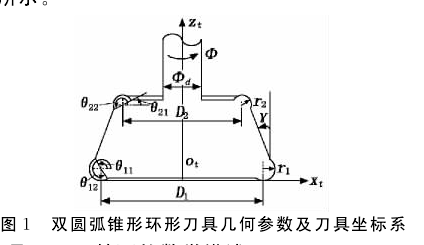
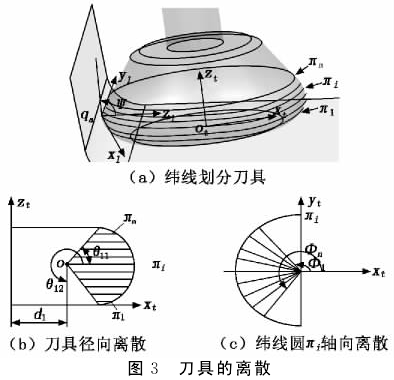
    图１为双圆弧锥形环形刀具几何参数及刀具坐标系。刀具被定义在刀具坐标系Ｓｔ（ｘｔ，ｙｔ，ｚｔ）中，ｚｔ轴为刀轴位置，ｘｔ轴通过刀具底面中心ｏｔ且垂直于ｚｔ轴，整个坐标系由右手法则决定。其中，ｒ１为刀具下圆角半径，ｒ２为刀具上圆角半径，Ｄ１为刀具底端的直径，Ｄ２为刀具顶端的直径，［θ１１，θ１２］为下圆弧的张角范围，［θ２１，θ２２］为上圆弧的张角范围，Φ为轴向转角；γ为刀具锥角，即刀具侧刃母线与刀轴间的夹角，令γ＜９０°。通过调整刀具参数，可实现利用刀具上的不同母线段与组合曲面的不同区域接触，从而减小刀具－工件之间的同时接触长度，适应组合曲面的加工需求，如图２所示。

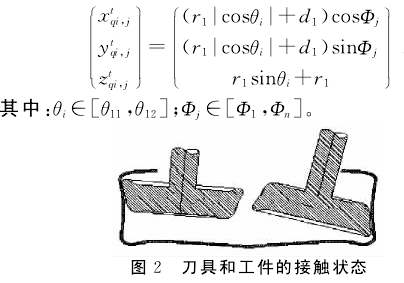
　　２刀具刃口回转面的数学描述为了建立刀具回转面的数学描述，需将刀具进行离散，本文采用纬线法划分刀具，如图３所示。根据编程公差δ的要求，一系列和刀轴垂直的平面与刀具工作面相交，将刀具工作面划分成ｍ个纬线圆π１，…，πｉ，…，πｍ；在ｘｔｚｔ平面内令θ为刀具纬线圆的径向离散角，则每个纬线圆πｉ对应圆心ｏ的张角为θｉ＝θ１１＋（θ１２－θ１１）·ｉ／（ｍ－１）；在ｘｔｙｔ平面内纬线πｉ在靠近工件的Φ＝Φｎ－Φ１范围内按照精度要求均匀离散为ｎ个点，每个离散点对应的轴向角度为Φｊ＝Φ１＋（Φｎ－Φ１）·ｊ／（ｎ－１）（ｊ＝１，２，…，ｎ），从而将纬线圆πｉ离散为点集合｛ｑｉ，ｊ，（ｉ＝１，２，…，ｍ；ｊ＝１，２，…，ｎ）｝，据此可以建立刀具上的离散点ｑｉ，ｊ在刀具坐标系Ｓｔ下的表达式为：

　　

　　３刀具定位方法

    为了在工件曲面上定位刀具，须建立刀具局部坐标系和工件局部坐标系（见图３（ａ））。取刀具母线上点ｑａ建立刀具局部坐标系Ｓｌ（ｘｌ，ｙｌ，ｚｌ），ｘｌ为ｑａ点的单位切矢，ｚｌ为该点的单位内法矢，ｙｌ通过右手定则得出。设ｚｌ轴和竖直方向的夹角为Ψ角，从刀具坐标系Ｓｔ转换到刀具局部坐标系Ｓｌ需要经过一次平移变换和旋转变换，其中平移变换是将刀具坐标系原点ｏｔ平移到ｑａ点上。则刀具上的离散点ｑｉ，ｊ在刀具局部坐标系Ｓｌ（ｘｌ，ｙｌ，ｚｌ）下可以表示为：

　　

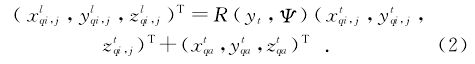
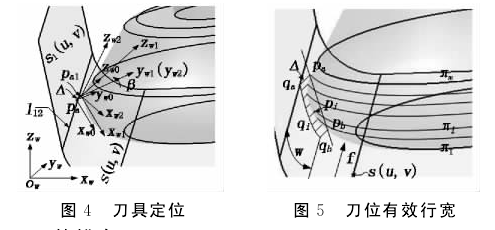
　　设ｓｌ（ｕ，ｖ）和ｓ（ｕ，ｖ）之间的切线是ｌ１２，令ｌ１２为第一行刀轨的导动线（如图４所示），在ｌ１２上选择工件第一参考点ｐａ建立工件局部坐标系Ｓｗ０（ｘｗ０，ｙｗ０，ｚｗ０）ｐａ点沿走刀方向的单位切矢为ｙｗ０，曲面在该点的单位法矢为ｚｗ０，根据右手定则得到ｘｗ０；设加工误差为Δ，再在ｐａ点外法线方向上拾取一个到该点距离为Δ的点ｐａ１作为工件第二参考点建立工件第二坐标系Ｓｗ１（ｘｗ１，ｙｗ１，ｚｗ１），且坐标系Ｓｗ１和坐标系Ｓｗ０平行；将工件第二坐标系Ｓｗ１（ｘｗ１，ｙｗ１，ｚｗ１）绕着ｙｗ１逆时针旋转β角得到工件第三坐标Ｓｗ２（ｘｗ２，ｙｗ２，ｚｗ２），此时，令Ｓｗ２系和Ｓｌ系重合就实现了刀具在工件上的定位。

　　４行宽求取

    在刀具完成定位后，即可求出刀位处的有效行宽，如图５所示。求取每个纬线圆πｉ上到曲面ｓ（ｕ，ｖ）距离最短的点作为特征点ｐｉ以及各特征点ｐｉ在曲面ｓ（ｕ，ｖ）上的垂足点ｑｉ。已知ｐａｑａ之间的距离为加工误差Δ，ｐａ为当前刀位的左端点，向右搜索满足ｐｉｑｉ＝Δ的点作为右端点ｐｂ。左端点ｐａ、右端点ｐｂ所对应的垂足点ｑａｑｂ之间的距离在走刀方向ｆ上的投影即为该刀位的行宽，表示为：

　　ｗ＝｜ｑａｑｂ×ｖｅｆ｜．（３）其中：ｖｅｆ为走刀方向ｆ上的单位矢量.

　　

　　５刀轨排布

    当刀位有效行宽所对应的两个端点位置确定以后，就可以方便地规划下一行刀轨了。将一行刀轨的导动线均匀离散成一定数目的点，按照上述方法求得每个刀位的行宽，根据该行刀轨行宽最窄的刀位右端点确定该行刀轨的实效右边界，将该实效右边界作为下一行刀轨的导动线，离散该导动线确定下一行刀轨上每个刀位左端点的位置。依次类推，直到将刀轨遍布整个工件曲面，加工结束。

　　６算法验证

    根据上述理论推导，在ＵＧ二次开发平台上编写了相关程序，并以某叶片为例对算法进行验证。

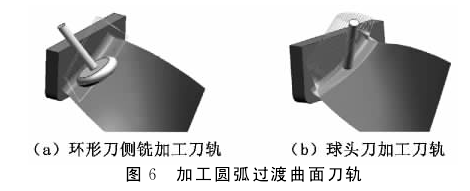
　　首先利用本文提出的算法，使用底端直径为Φ１２ｍｍ，下圆角半径为２ｍｍ的环形刀，加工圆角过渡面只需要３行刀轨，见图６（ａ）。然后使用直径为Φ６ｍｍ的球头刀，利用ＵＧ中的算法计算，需要１５行刀轨，见图６（ｂ）。因此可知本文提出的环形刀侧铣加工算法相对于常用的球头刀算法效率上提高了５倍。

　　７结论

    本文开发的利用刀具不同部分加工曲面不同区域的刀位优化方法，有效控制了刀具与工件接触区宽度，实现选择性接触和加工；利用环形刀加工圆弧过渡面，将刀位优化、刀轨规划统一起来，增强了编程的自动化。计算实例表明该方法可以精确、快速生成刀具轨迹，实现圆弧过渡区域的高效加工。

　　

　　参考文献：

　　[1]Tsai M D,Takata S,Lnui M,et al.Operation planningbased on cutting process models[J].Annals of the CIRP,1991,40（1）：95-98.
　　
　　[2]Blackmore D,Leu M C,Wang L P.The sweep-envelopedifferential equation algorithm and its application to NCmachining verification[J].Computer-Aided Design,1997,29（9）：629-637.
　　
　　[3]Hatna A,Grieve R J,Broomhead P.Automatic CNCmilling of pockets:geometric and technological issues[J].Computer Integrated Manufacturing Systems,1998,11（4）：309-330.
　　
　　[4] 李志兵，陈志同。基于环面刀具的叶片过渡区域宽行加工技术[J].航空学报，2011,25（9）：1722-1731.
　　
　　[5] 黄魏。叶片圆弧过渡曲面宽行加工技术研究[D].北京：北京航空航天大学，2010:8-38