中国数学史研究方法论的反思

　　摘    要：　自李俨、钱宝琮始,国内外学者开始用现代数学方法整理古代数学遗产,并建立了中国数学史学科的研究范式。20世纪80年代起,吴文俊倡导对于中国古代数学的“古证复原”,提出了数学史研究“古为今用”的目标。今天的中国数学史研究正向广度与深度两方面拓展。从数学史研究的方法论来看,存在三个互相关联并需要反思的理论议题。第一,辉格解释问题,其实质在于探究现代数学对古代数学的解释限度;第二,史料问题,其目的在于探讨古代数学实作传统的多样性;第三,古为今用问题,它与前两个议题及数学史的学科定位有关。数学史的研究实践正通过独有的方式探讨上述议题,因此长期存在于研究中的内史与外史之争论是没有必要的。

　　关键词：　中国数学史; 方法论; 辉格解释; 史料; 古为今用;

　　Abstract：　Since Li Yan and Qian Baocong,Chinese and international scholars have started to use modern mathematics to discover ancient mathematical heritage and have therefore established the research paradigm for the discipline of the history of Chinese mathematics.Since the 1980s,Wu Wenjun has advocated “the reconstruction of ancient proofs” for ancient Chinese mathematics and proposed the research aim for the studies in the history of Chinese mathematics as “making the past serve the present”.Nowadays,research in the history of Chinese mathematics is carried out towards the extension in areas and depth.From the perspective of methodology,there are three correlated theatrical issues that need to be reflected on.The first one is the Whig interpretation problem whose nature is to study the limitation of modern interpretation of ancient mathematics.The second one is the sources problem whose aim is to study the diversity of mathematics in the ancient world.The last one is the problem of making the past serve the present,which is closely related to the two previous issues and to the disciplinary position of the history of mathematics.The research carried out in history of mathematics is discussing these issues in its own way;hence the long-term dispute on the internal history and the external history in the studies of the history of mathematics is not necessary.

　　Keyword：　History of Chinese mathematics; Methodology; Whig interpretation; Sources; Making the past serve the present;

　　算学是中国一个具有悠久历史的学科。明清以降,中国传统数学逐渐融入现代数学之中,整理古代数学遗产便成为一项时代赋予学人的历史性任务。李俨、钱宝琮最先用现代数学方法整理中国古代数学遗产,引领了国内外学界的研究潮流,开创了中国数学史学科的研究范式。[1]20世纪80年代起,吴文俊倡导研究中国古代数学的“古证复原”方法,并创造性地吸取中国古代数学的机械化、构造性特色,提出“数学机械化”思想,实现了“古为今用”的目标。[2,3]2010年,郭书春主编《中国科学技术史·数学卷》,基本囊括了自李、钱二位先贤以来的中国数学史研究成果,可以说为之做一总结。[4]

　　与此同时,学界也一直很关注数学史研究的方法论。吴文俊提出“古证复原”应遵守的三项原则,并将之运用于对《海岛算经》的研究,反思和推进了中国数学史的研究方法。([2],p.162)曲安京认为20世纪的中国数学史研究是由李俨与钱宝琮领导的“发现”范式转变为吴文俊领导的“复原”范式,并提出“为什么数学”的研究期望。[5,6]孙小淳认为这种划分方法值得商榷。[7]张东林认为为了摆脱辉格的研究倾向,数学史应转变为一门思想史。[8]鞠实儿、张一杰认为中国数学史研究存在“据西释中”与“据中释中”两条路线,他们赞成后者并进而以“刘徽割圆术”为例提出了中国数学史的本土化研究程序。[9]法国学者林力娜(Karine Chemla)认为在数学史研究中应对“什么是数学”持有开放、多元的观念,[10,11]这一观点也得到了研究其他数学文明的国际数学史家们的赞同。[12,14]([13],p.7);([13],p.519)这些看法都表明了中国数学史研究者期望在总结学界既有研究成果的基础上更好前进的美好愿望。

　　近年来,笔者的中国数学史研究主要集中于如下两个方面:第一,以筹算为中心研究汉唐筹算复原、宋元筹算文本化、明代筹算向珠算转变等议题,揭示出物质与数学思想之互动;[15,16,17,18,19]第二,以儒家经典中的数学文献为中心研究儒家算法传统及其历史演进等议题,揭示出中国古代数学的多样性。[20,21,22,23,24,25,26,27,28,29]在此基础上,结合国际数学哲学界近年来对于数学实践与数学文化多样性的研究思潮,[30]笔者对于数学史研究方法论有了一些新思考,并认为“辉格解释问题”、“史料问题”与“古为今用问题”是三个互相关联并需要反思的理论议题。故在此文中,笔者将以对筹算的研究为例来试图回答“辉格解释问题”;将以对儒家经典中数学文献的研究为例来试图回答“史料问题”;并在此基础上来分析和解答“古为今用问题”。
 

 

　　一、辉格解释问题

　　今天的学界对于数学史研究辉格倾向的批判已经比比皆是。例如施泰德尔(Jacqueline Stedall)在一本介绍数学史的小册子的开头便指出了这个问题:

　　第一个问题就是一些解释往往描绘了一个辉格版本的数学史。在这一版本之中,数学知识通常是被认为是不断向前向上朝着今天的辉煌成就进步。不幸的是,那些寻求进步证据的人们倾向于忽视数学发展中的复杂性、过失和彻底的失败。而这些是包含数学事业在内的任何人类的尝试所不可避免的一部分;有时失败也可以像成功一样揭示真相。此外,通过把今天的数学定义为描述以前努力的基准,我们太容易忽视过去的贡献,如勇敢的但最终过时的努力。与此相反,在仔细考察这个事实或那个理论是如何起源的,我们需要看他们在自身时空的语境中的发现。[31]

　　施泰德尔在此简明地指出了辉格数学史的问题:一方面是忽视了数学发展中的复杂性和今天看来失败和过时的东西,另一方面是无法弄清数学发展的起源与过程。她认为只有通过历史语境的考察才能了解某项数学知识的起源。实际上,这种带有进步观念的辉格史可以从哲学意义上理解为柏拉图主义[32]——即古巴比伦数学史家罗伯森(Eleanor Robson)所说的:历史学家从历史记录中甄别出“柏拉图的数学对象”,并且用今天对应的数学术语描述之。在此意义上,数学家是发现数学真理,而数学史家则是发现历史记录中的对应部分。对此,古埃及数学史家伊姆豪森(Annete Imhausen)则批评地指出为不应采取“只有一种数学”的哲学立场。[33]

　　然而,虽然辉格的数学史受到了严厉地批判,但是在数学史中完全排除辉格解释也是不可能的。从理论上讲,这是因为如果彻底采取反辉格立场,即不用今天的数学去理解过去的数学,那么等于承认古今数学是两种完全不同的、不具有可通约性的学问。在此意义上,如何解释数学的历史具有连续性?而且,如果所有的数学知识都必须考虑其历史语境,那么这就将划向科学知识社会学“强纲领”下的知识建构论,从而彻底消解数学的真理性。这似乎也违反了我们的普遍直觉和历史经验。

　　其实,从数学史的研究实践来看,辉格与反辉格的数学史都有其存在的必要性。一方面,虽然数学史家意识到古代数学有其特色,现代数学对之的解释能力不是无限的,但是在研究中彻底排除现代数学、不使用印度阿拉伯数码和+、-、×、÷等符号也是做不到的——现代数学在一些方面看来总具有一定的解释力。另一方面,由于辉格的数学史往往倾向于将古代数学解释为现代数学的低级阶段,从而确实丧失了研究进一步的可能性,因此值得警惕。正如罗伯斯在评价1950年代巴比伦数学史研究遇到的问题时说:“一旦解释被做出了,即古代文献被用现代符号重写之后,就没有任何可说的了。这个领域(即巴比伦数学史研究)便停滞了几十年。”[14]

　　综上,笔者认为无论从理论还是实践的角度,辉格解释问题的实质都在于现代数学对古代数学解释的限度——即辉格与反辉格之间的张力。如果我们可以知道此限度,那么所谓的“柏拉图主义”便可以消解了——限度之内,可以以今释古;限度之外,则不可以。当然,无论是数学哲学的理论探讨还是数学史的研究实践都没有明确地告诉我们这一问题的解答。

　　在上述分析的基础上,笔者认为数学史研究既不可能不预设立场,也不能僵硬地站定辉格或反辉格的立场;数学史研究的理论预设必须是灵活的,只能根据研究成果来不断改进立场,从而自下而上地推进我们对于的数学的理解。具体而言,在研究的过程中,我们只能先假定所研究的那部分数学知识是不可以用辉格解释的,而其他并非研究目标的数学知识是可以辉格解释的,由此开展研究。换言之,采取辉格还是反辉格的立场实际上取决于数学史家的研究语境。

　　具体而言,我们知道从历史的角度而言,中国人行用印度阿拉伯数字很晚,因此一般来说不该将之应用于对中国古代数学的研究之中。但是,如果研究的目标不在数制、数码,那么阿拉伯数字就应该是可以用的。反之,如果我们研究的目标是分析中国筹算、汉字数字及其算法之特色,那么当然阿拉伯数字就不应出现在对应的解释之中。[15]同样地,如果我们研究的目标是表明某个筹算操作的算法,那么用现代数学符号表明其运算过程自然就是不可接受的。但是,如果我们只是为了表明某个筹算算法结果的正确性,或者为了突出该算法与其他算法的差异性,那么现代数学符号的解释在某种程度上就是可接受的。[16]

　　让我们以对《九章筭术》方程章第七题的分析为例更清楚地说明上述观点。该题云:

　　今有牛五、羊二,直金十两;牛二、羊五,直金八两。问:牛、羊各直金几何?

　　荅曰:牛一直金一两二十一分之一十三,羊一直金二十一分两之二十。

　　术曰:如方程。([34],pp.359-360)

　　此题流行的解释为:设一牛值x金,一羊设y金,则据题可列出方程组:

　　消元后解之得:

　　这一流行解释无疑是以今释古的、辉格的,其优缺点都非常明显:它可以给出该题基本等价的现代数学信息,即题设的方程组与答案,却无法告知读者该题所反映的古人的运筹操作过程。因此,如果我们的研究目的在于表明《九章》算法的正确性,而不在于揭示其筹算操作,那么这一解释在一定程度上是可以接受的。而之所以说在一定程度可接受,是因为在筹算的语境中,正确性可能包括了更多超出今天数学的历史内容(如运筹的简约性等)。实际上,在各种数学史论着中,这一类解释往往最先给出,以给读者一个直观的印象。与此相反,如果我们的研究目标在于展现其背后蕴藏的筹算操作信息,则很明显我们不应接受该解释,而应该以筹算刻画之。

　　当我们分析该问刘徽注(263年)时,上述观点会更加凸显。刘徽云:

　　假令为同齐,头位为牛,当相乘。右行定,更置牛十,羊四,直金二十两;左行牛十,羊二十五,直金四十两。牛数等同,金多二十两者,羊差二十一,使之然也。以少行减多行,则牛数尽,惟羊与直金之数见,可得而知也。以小推大,虽四、五行不异也。([34],p.360)

　　刘徽实际给出了具体的筹算操作信息。如果我们研究的目的在于揭示该信息,则不宜使用现代数学符号;但又由于我们的研究目标不在于表明筹算数字之特色,则在此处可以用印度阿拉伯数字替代之。因此宜将整个过程表为[16]:

　　上述过程中的印度阿拉伯数字可以替换相应的筹算。由此可见,虽然使用了印度阿拉伯数字,但是很显然这一解释不是完全按照现代数学的,而在某种程度上揭示了刘徽注的筹算操作。因而,实际可以说根据研究需要融合了辉格和反辉格研究立场。

　　总之,从数学史的研究实践来看,数学史家实际是在不同的研究语境中根据研究需要灵活采用了辉格或反辉格立场。就此而言,对辉格数学史的批评是不够客观和公正的。虽然在数学史的研究中有反辉格意识是十分必要的,但彻底的反辉格既无可能,也非必要。如果说反辉格的数学史研究有利于揭示古代数学的特色,那么我们也可以说辉格研究有利于发现古今数学相通之处。因此,数学史的研究实践正在提供这样一种可能性——通过全面分析历史上的数学知识,我们可以辨别哪些数学知识是不随时空转变的真理,哪些数学知识是易变的语境知识,由此自下而上探究辉格解释问题。

　　二、史料问题

　　从学理上讲,数学史是历史学的一部分,是基于原始文献的研究。中国数学史的学者们多次表明了原始文献的重要性。[35,36,37]然而,以往的中国数学史研究往往集中于所谓的数学文献(如《九章算术》),而较忽视其他载有数学知识的文献(如儒家经典中的数学文献)。事实上,这两类文献的差别也被研究其他数学文明的学者观察到,如罗伯森说:

　　必须在两种文本之间做一个区分:一种是有数学兴趣的文本,即今天的数学史家、计量史家或度量衡史家会对其内容感兴趣;另一种是原初就关于数学的文本,即这些文本被写下来的目的就是为了交流或记载数学技术或者指明一个数学算法的实施。([38],p.7)

　　罗伯森所作的这一区分十分重要,指出了所谓数学文献与非数学文献都载有数学知识,都是数学史研究的对象。伊姆豪森也接受了这一区分([33],p.41)。在对于两河流域数学史的研究中,这两类文献或许有较为平衡的研究,但是在中国数学史的领域中,无疑以《九章算术》及《算经十书》为代表的算学经典占据了主导。

　　具体而言,我们可以说研究秦及先秦数学的主要文献是汉简《算数书》、秦简《数》、《墨经》中的相关记载,研究汉至唐代的数学主要是依靠《算经十书》,研究宋元数学则凭借贾宪、秦九韶、李冶、杨辉、朱世杰等人的着作,研究明清数学就是靠明清算家的着作。这一凭借算书进行中国数学史研究的做法取得了丰硕的成果——认识、复原古代数学,揭示了影响其发展的各种因素。[4]然而,很明显这一研究进路主要是以所谓“内史”为主,较少考虑其历史语境,由此兴起了所谓数学史的“外史”研究。

　　实际上,在此意义上,无论是内史还是外史,都默认了“(一个时代)只有一个数学”的哲学立场——而那一个数学就是那个时代核心数学文献中所记载的知识。笔者认为既然学界对于辉格解释有疑虑,我们只能先假定人类在不同时空中的不同实践活动都可能产生有所不同的数学知识,是不同的数学实作(mathematical practice),而这些数学知识与实作可能会被不同类型的文献所记载。由此,我们可以极大地拓展数学史的研究文献,并可能通过分析研究这些众多文献,更全面地复原古代数学原貌,从另一角度探讨辉格解释问题。

　　具体而言,原先的中国数学史研究集中于传统算书,揭示了中国古代筹算数学的历史发展;在谈到数学与儒学的关系时,也是以算书为主,考察其中的儒学思想。这样的做法实际上是把中国古代数学局限在算书的范围之内,从而限制了我们进一步理解古代数学及其与儒学的关系。通过分析儒家经典中蕴藏的数学文献,我们可以发现其中的数学知识与实践与以《九章算术》为代表的筹算传统不同——尤其是前者几乎不使用算筹,从而揭示出不为学界所知的儒家算法传统。[21,25],[27]在此基础上,我们就知道数学与儒学的关系并不如以往设想的简单——儒家经典中的数学传统是儒学的一部分,而算家的数学传统则是相对独立之内容。[22,23,24],[26,28]-[29]

　　让我们以初唐学者贾公彦(7世纪)对《周礼·考工记》“参分弓长,以其一为之尊”的注疏为例,来凸显上述观点。[21]该段注疏中,贾公彦先基于郑玄注称述一个勾股问题,进而给出算法:

　　……凡筭法:以蚤低二尺,即以低二尺为句。又以持长四尺为弦,又蚤末直平者为股。弦者四尺,四四十六,为丈六尺。句者二尺,二二而四,为四尺。欲求其股之直平者。筭法:以句除弦,余为股。将句之四尺除弦,丈六尺中余四尺,仍有丈二尺在。然后以筭法约之。([39],p.910)

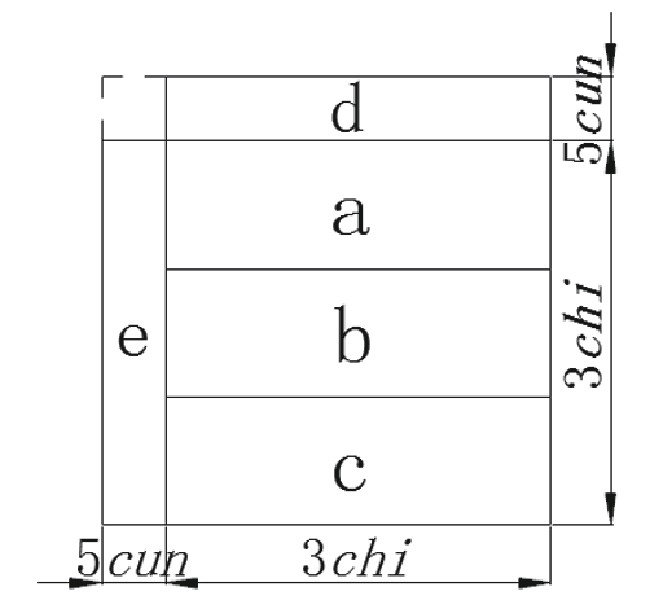
　　贾公彦计算的勾股问题即勾长二尺、弦长四尺,求其股。贾氏的做法是先将二尺平方得四尺,四尺平方得十六尺即一丈六尺。注意到这里贾公彦运用了古人独特的以长度表示面积的做法,即把4平方尺表示为一个宽1尺、长4尺的长方形,把16平方尺表示为一个宽1尺、长1丈6尺(=16平方尺)的长方形。两者相减为一丈二尺,即宽1尺、长1丈2尺的长方形,为股的平方。(图1)贾公彦继云:

　　广一尺,长丈二尺,方之。丈二尺,取九尺,三尺一截,相裨得方三尺。仍有三尺在。中破之为两段,各广五寸,长三尺。裨于前三尺方两畔,畔有五寸。两畔并前三尺,为三尺半。角头仍少方五寸。不合不整三尺半。几,近也,言近半。([39],p.910)

　　在这段中,贾氏通过切割操作把宽1尺、长1丈2尺的长方形转化为一个正方形,即所谓“方之”。他先切下宽1尺、长9尺的一部分,拼接成3尺之方。接着将剩下的宽1尺、长3尺的小段分为宽5寸、长3尺的两部分,再并于3尺之方的两端。由此完成了操作,见图1-2。贾氏的做法实际等于是把12平方尺开方理解为将之转化为一个正方形,其边长即为所求值(小于3.5尺),这一操作过程不使用算筹。(图2)而且,贾氏对开方运算不理解为“已知正方形面积求其一边”,而是理解为“已知长方形面积求其相同面积正方形的边”,这些都是传统算书中所未见的。笔者在其他时代学者对于儒家经典的注疏中也发现了具有相同思想的算法,这说明贾氏的做法具有一般性,展现了儒家的算法传统,也表明原先学界认为筹算开方术一统天下的看法是不正确的。[26]

　　图2  方之

　　图1  丈二尺

　　除此之外,数学史文献的拓展还可以通过视角的转换来完成。通常,对于文献内容的分析是站在作者的视角,而较少从读者视角来考察数学知识的传播与实际效果。事实上,数学作为一项公共事业,个别天才的数学家或经典着作固然重要,这些发现能否被继承或被公众了解也是另一个重要面向。因此,有必要更广泛地利用文献、从读者视角分析文献内容。例如,以往学界都认为明末利玛窦与李之藻合作编译的《同文算指》传入了西方笔算。通过分析时人孙元化对珠算与西方笔算的比较,可以发现时人倾向于用珠算来解决加减问题;这一倾向与分析《同文算指》文本所得结果一致。因此,我们可以知道尽管两位作者力图传入西方笔算,但受限于文化历史背景,当时的读者所接受到的知识实际是以珠算辅助笔算。[19]

　　总之,数学史研究没有必要局限于“数学文献”,而应广泛地大力拓展研究文献,探讨不同文献中记载的数学知识之特色与共同点。就此而言,如果说辉格解释问题是在探讨古今数学之异同,史料问题则是帮助我们全面深入了解某一时代数学实作的多样性,从而深化我们对于数学的理解。

　　三、古为今用问题

　　从理论上,作为历史学一部分的数学史具有了解数学、探索发展规律、为数学教育服务等多种功能。[40]在所有的功能中,数学史的“古为今用”可能是学界最看重的。1975年,吴文俊以“顾今用”为笔名在《数学通报》上发表了《中国古代数学对世界文化的伟大贡献》。之后“逐步开拓出一个既有浓郁的中国特色,又有强烈的时代气息的数学领域——数学机械化,树立了古为今用的典范”。[41]吴先生对之总结道:

　　假如你对数学的历史发展,对一个领域的发生和发展,对一个理论的兴旺和衰落,对一个概念的来龙去脉,对一种重要思想的产生和影响等这许多历史因素都弄清了,我想,对数学就会了解得多,对数学的现状就会知道得更清楚、深刻,还可以对数学的未来起一种指导作用,也就是说,可以知道数学究竟应该按照怎样的方向发展可以收到最大的收益。([41],p.4)

　　吴先生之所以可以实现古为今用的目标,是基于他对于数学的深刻认识。他意识到筹算的构造性与机械化特色,也意识到它的局限。[33]例如他说:

　　“由于当时用筹算,方程各不同类型项的系数须布置在算盘特定的位置来进行运算,因而未知数的个数只能限于四个。如果改用纸笔运算,则四个未知数的限制完全可以打破。至于原来四元术的原理与方法,则仍可以适用于解任意多个未知数的高次联立方程组。”([42],pp.38-39)

　　他认为数学发展的三个阶段是“筹算、笔算和机算”。[43]正是在这样的认识下,他发现可以筹算与机算的某些相似性,为“古为今用”做好了准备。

　　由此可见,已经经过历史筛选的古代数学不太可能被简单地挪用到今天来。为了实现“古为今用”,需要满足相当高的要求,其中重要的一条便是——深刻理解到古代数学的某些可以为今天所用的本质(如中国古代数学的机械化特性)。2017年,林力娜在欧洲数学大会上做大会报告,从中国古代数学切入谈到数学文化的多样性,进而呼吁数学家与历史学家的合作,认为这种合作不仅对历史学家是有益的,也可能对今日数学提供某些有趣的洞见。[44]很显然,这种未来可能存在的“古为今用”,也不是简单地挪用中国古代数学,而是必须基于对数学文化多样性的深入理解,而且同样必须有当代数学家的参与。

　　总之,从实践来看,数学史的“古为今用”是可能的,但必须具备相当高的条件:第一,数学史家通过深入的历史研究尽可能地将历史上数学知识与实践的多样性保存下来——虽然有些数学知识已经被历史淘汰了(如中国古代对筹算的使用或者印度数学中对于除数为零的探讨等),但谁又能保证将来它们不会再以另一形式“复活”呢?第二,数学家运用洞察力发现历史上数学的某些可为今天所用的本质特征,从而以之发展今天的数学,实现古为今用。在此意义上,数学史的“古为今用”必然是极具现代意识的数学史家与极具历史意识的数学家的完美合作。

　　然而,如果我们把“古为今用”的“今用”不限定于现代数学,那么这一问题实际还与数学史的学科定位有关。由于数学史研究所揭示的数学历史发展之复杂性,远非今天数学可以涵盖;所以笔者认为数学史不应安于“数学次一级研究”的位置,而是应该努力与数学一道,成为人类知识大厦的基础。从实际的角度看,在跨学科交流合作研究繁盛的今天,数学史研究不仅与历史、哲学、逻辑学等学科都有密切的关联,而且往往成为后面这些学科研究的基础知识。[45]如同数学作为自然科学的基础一样,未来的数学史可以作为人文社科的基础。在此意义上,数学史的“古为今用”自然是不成问题的。

　　四、结 语

　　综上所述,数学史研究中辉格解释问题的实质是探讨古今数学本质之异同,史料的多元性引导我们深刻理解古代数学的多样性,古为今用问题则期待在此基础上发展今天的数学,亦涉及数学史的学科定位问题。三者是互相关联而又各有侧重的议题。对三者的反思说明中国数学史研究应在史料与方法上有新的思考和突破。

　　以往对于数学史研究的分析往往采用与科学史相同的“内史——外史”的框架分析方法。这种科学史编史学中的分析方法过度简单化了数学史的研究实践,将之固定在内史或外史位置上,从而往往成为一种学术评论技巧,实则阻碍了数学史研究的开展。从本文的分析看,数学史研究者应站在前人的研究基础上,从原始文献出发,采取灵活的哲学立场,兼具历史眼光与现代意识,分析数学发生、发展与被书写、被实作的历史语境,以期深刻揭示数学及其历史发展之本质。这样一种做法从实践的角度消解了内史与外史之争论,展现了数学史研究的复杂性与多元功能,预示了该研究的美好未来。

　　参考文献

　　[1]李俨、钱宝琮.李俨、钱宝琮科学史全集[M].沈阳:辽宁教育出版社,1998.
　　[2]吴文俊.《海岛算经》古证探源[A],吴文俊:《九章算术》与刘徽[C],北京:北京师范大学出版社,1982,162-180.
　　[3]吴文俊.从《数书九章》看中国传统数学构造性与机械化特色[A],吴文俊:秦九韶与《数书九章》[C],北京:北京师范大学出版社,1987,73-88.
　　[4]郭书春.中国科学技术史·数学卷[M].北京:科学出版社,2010.
　　[5] 曲安京.中国数学史研究范式的转换[J].自然科学史研究,2005,26(1):50-58.
　　[6]曲安京.再谈中国数学史研究的两次运动[J].自然辩证法通讯,2006,28(5):100-104.
　　[7]孙小淳.数学视野中的中国古代历法——评曲安京着《中国历法与数学》[J].自然科学史研究,2006,25(1):83-89.
　　[8]张东林.数学史:从辉格史到思想史[J].科学文化评论,2011,8(6):26-41.
　　[9] 鞠实儿、张一杰.中国古代算学史研究新途径——以刘徽割圆术本土化研究为例[J].哲学与文化,2017,44(6):25-51.
　　[10]林力娜.数学证明编史学中的一个理论问题[J].科学文化评论,2011,8(3):16-25.
　　[11] Karine,C.'Historiography and History of Mathematical Proof:A Research Programme'[A],Karine,C.(Ed.) The History of Mathematical Proof in Ancient Traditions[C],Cambridge:Cambridge University Press,2012,1-68.
　　[12]Sabetai,U.'On the Need to Rewrite the History of Greek Mathematics'[J].Archive for History of Exact Sciences,1975,15(1):67-114.
　　[13] Victor,K.The Mathematics of Egypt,Mesopotamia,China,India and Islam:A Sourcebook[M].New Jersey:Princeton University Press,2007.
　　[14] Eleano,R.Mathematics in Ancient Iraq:A Social History[M].New Jersey:Princeton University Press,2008.
　　[15]朱一文.再论《九章算术》通分术[J].自然科学史研究,2009,28(3):290-301.
　　[16] 朱一文.数:筭与术——以九数之方程为例[J].汉学研究,2010,28(4):73-105.
　　[17] 朱一文.数学的语言:筭筹与文本——以天元术为中心[J].九州学林,2010,(4):81-103.
　　[18]朱一文.秦九韶对大衍术的筭图表达——基于《数书九章》赵琦美钞本(1616)的分析[J].自然科学史研究,2017,36(2):44-257.
　　[19] Zhu,Y.W.'How Were Western Written Calculations Introduced into China?—An Analysis of the Tongwen suanzhi (Arithmetic Guidance in the Common Language,1613)'[J].Centaurus,2018,60(1-2):69-86.
　　[20]朱一文.儒家经典中的数学知识初探——以贾公彦对《周礼·考工记》“?氏为量”的注疏为例[J].自然科学史研究,2015,34(2):131-141.
　　[21]Zhu,Y.W.'Different Cultures of Computation in Seventh Century China from the Viewpoint of Square Root Extraction'[J].Historia Mathematica.2016,43(1):3-25.
　　[22]朱一文.再论中国古代数学与儒学的关系——以六至七世纪学者对礼数的不同注疏为例[J].自然辩证法通讯,2016,38(5):81-87.
　　[23]朱一文.初唐的算学与礼学——以诸家对《礼记·投壶》的注疏为例[J].中山大学学报(社会科学版),2017,57(1):160-168.
　　[24] 朱一文.算学、儒学与制度化——初唐数学的多样性及其与儒学的关系[J].汉学研究,2017,35(4):109-134.
　　[25] 朱一文.朱熹的数学世界——兼论宋代数学与儒学的关系[J].哲学与文化,2018,45(11):167-182.
　　[26]朱一文.儒家开方算法之演进——以诸家对《论语》“道千乘之国”的注疏为中心[J].自然辩证法通讯,2019,41(2):49-55.
　　[27]朱一文.从度量衡单位看初唐算法文化的多样性[J].中国科技史杂志,2019,40(1):1-9.
　　[28]朱一文.宋代的数学与易学——以《数书九章》“蓍卦发微”为中心[J].周易研究,2019,32(2):81-92.
　　[29]朱一文.明清之际的数学、儒学与西学——以黄宗羲的数学实作为中心[J].内蒙古师范大学学报(自然科学汉文版),2019,8(6):538-544.
　　[30] Brendan,L.Mathematical Cultures:The London Meetings 2012-2014[M].Switzerlandp:Springer International Publishing,2016.
　　[31] Jacqueline,S.The History of Mathematics:A Very Short Introduction[M].New York:Oxford University Press,2012.
　　[32] Robert,B.J.Philosophy of Mathematics:A Contemporary Introduction to the World of Proofs and Pictures.Second Edition[M].New York:Routledge,2008.
　　[33] Annette,I.Mathematics in Ancient Egypt,3200 BC–AD 395:A Contextual History[M].Mainz:Johannes Gutenberg Universit?t.2008,7-9.
　　[34] 郭书春.汇校《九章筭术》(增补版)[M].沈阳:辽宁教育出版社,2004.
　　[35]李俨.中国古代数学史料[M].北京:中国科学图书仪器公司,1954.
　　[36]郭书春.尊重原始文献避免以讹传讹[J].自然科学史研究,2007,26(3):438-448.
　　[37]郭书春.认真研读原始文献——从事中国数学史研究的体会[J].自然科学史研究,2013,32(3):332-346.
　　[38] Eleanor,R.Mesopotamian Mathematics,2100-1600 BC:Technical Constants in Bureaucracy and Education[M].Oxford:Clarendon Press.1999.
　　[39] 阮元.十三经注疏[M].北京:中华书局,1980.
　　[40] 梁宗巨.世界数学通史(上册)[M].沈阳:辽宁教育出版社,1995,8-19.
　　[41]李文林.古为今用的典范——吴文俊教授的中国数学史研究[J].北京教育学院学报,2001,15(2):1-5.
　　[42] 吴文俊.对传统数学的再认识[A],吴文俊:吴文俊论数学机械化[C],济南:山东教育出版社,1999,30-44.
　　[43]许寿椿.筹算、笔算、机算——数学发展阶段的一种新观察[A],王渝生:第七届国际中国科学史会议文集[C],郑州:大象出版社,1999,226-231.
　　[44]Karine,C.'The Diversity of Mathematical Cultures:One Past and Some Possible Futures'[J].Newsletter of the European Mathematical Society,2017,104:14-24.
　　[45]朱一文.再论数学史与数学哲学的关系[J].自然辩证法研究,2019,35(11):95-99.