道路与桥梁工程师论文(精选范文10篇)之第八篇
摘要:为了解高铁桥梁整体式减震榫的疲劳性能, 确定其低周疲劳寿命, 提出采用临界平面法和能量法组合的方法对减震榫的低周疲劳寿命进行预测。该方法以临界平面上的塑性应变能作为减震榫的疲劳损伤参量, 通过坐标变换法求得减震榫在给定榫顶水平位移下最大损伤平面上的塑性应变能, 然后根据塑性应变能与疲劳寿命之间的幂指数函数关系进行疲劳寿命预测。通过3个减震榫试样的低周疲劳试验验证该方法的准确性。结果表明:减震榫试样的低周疲劳预测寿命与试验寿命相差很小, 提出的方法能较准确地预测减震榫的低周疲劳寿命。
关键词:高速铁路桥; 减震榫; 低周疲劳; 疲劳寿命; 塑性应变能; 疲劳试验

1 引言
我国铁路桥梁普遍采用简支梁桥和重力式墩台。重力式墩台的刚度很大,在地震作用下很难进入塑性,因此依靠结构自身延性来耗散地震能量无法实现[1].为了提高铁路简支梁桥的抗震能力,近年来开发了新型的减隔震装置---减震榫。减震榫设置在主梁与桥墩连接处,因其具有较大的延性耗能能力,能够耗散大部分地震能量,所以可以有效地保护桥墩和上部梁体结构的安全。该减震系统已成功应用于高铁兰新线、宝兰铁路等建设中,体现了其良好的应用价值。但目前,我国关于减震榫设计和施工的规范还在制订过程中,尚需对其开展进一步的理论和应用研究。
李承根等[2]最早提出支座功能分离的减震设计理念,并初步研究了减震榫的结构形式以及对减震榫材料性能的要求。孟兮等[3]全面考察了整体式减震榫的强度、刚度、滞回性能及耗能能力等性能指标,并分析了减震榫在多跨铁路简支梁桥中的减震效果。李爱丽等[4]提出了分离式减震榫,并对其工作机理、性能参数及设计原则等进行了研究。Liu C等[5]研发了减震榫系统的防落梁装置,并对其滞回性能进行分析。以上学者的工作建立和完善了减震榫的应用体系,但对减震榫的疲劳性能尚未深入探讨,也未开展疲劳寿命预测方面的研究。
减震榫的工作状态为塑性耗能状态,在地震作用下往复运动直至发生低周疲劳破坏,低周疲劳寿命是减震榫非常重要的工作性能参数。本文从整体式减震榫的力学行为状态入手,提出以临界平面上的塑性应变能为疲劳损伤参数对减震榫的低周疲劳寿命进行预测,并通过低周疲劳试验验证该预测方法的准确性。
2 减震榫构造及力学状态
整体式减震榫采用延性较好的国产软钢制作,其结构自上而下可以分为顶部球形嵌入端、直线段、等强度段和底部法兰盘固定端。其中,等强度段采用圆形变截面,是减震榫的弯曲耗能部位。减震榫构造见图1.
根据减震榫活动支座的工作原理,榫身主要承受水平荷载,不承受竖向荷载。在顶端水平荷载作用下,减震榫横截面同时存在弯矩和剪力,即同时存在正应力和剪应力2个应力分量。对减震榫进行力学分析可知,横截面的正应力远远大于剪应力,剪切变形对减震榫顶端侧移的影响非常小。因此,对减震榫进行结构设计时可以忽略剪应力的影响,将其作为纯弯构件。但正应力和剪应力对疲劳裂纹的产生和发展都起作用,剪应力对疲劳裂纹的产生具有较强的驱动作用。因此,对减震榫进行疲劳分析时不宜忽略剪应力的影响,应按多轴疲劳考虑。
图1 减震榫构造

3 低周疲劳寿命预测方法
临界平面法是疲劳寿命预测的主要方法之一。该方法以材料或构件疲劳损伤最大的平面作为疲劳破坏临界平面,通过在临界平面上选择合适的疲劳损伤参量进行疲劳寿命的预测。临界平面上的损伤参量有应力、应变和能量3种。其中,以能量作为损伤参量更符合多轴疲劳的破坏机制。因此,本文将临界平面上的损伤参量引入到能量法疲劳寿命预测模型中,以解决减震榫的多轴疲劳寿命预测问题。
3.1 疲劳损伤参量确定
塑性应变能可以综合考虑应力和应变2个变量对疲劳的影响[6,7],因此以临界平面上的塑性应变能作为减震榫的疲劳损伤参量。
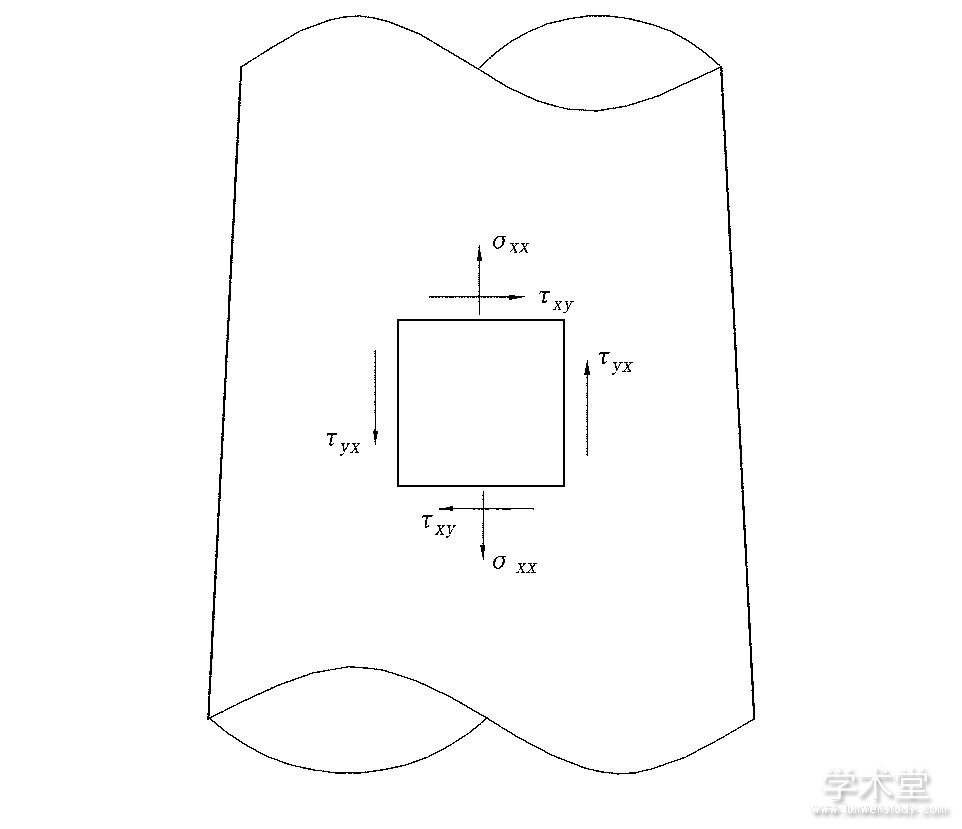
减震榫的主要耗能段为等强度段,在榫顶水平荷载作用下,等强度段内部会有拉压作用、剪切作用、纤维的挤压作用等,内部空间一点的应力应变响应由9个分量组成。在等强度段内部取一微小单元体,如果忽略对结构疲劳影响较小的分量,只考虑影响较大的正应力和剪应力,则其应力状态见图2.
在榫顶水平荷载作用下,一个荷载循环的塑性应变能为
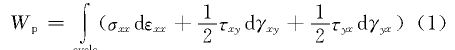
式中,σxx和εxx分别为临界平面上的正应力和正应变,τxy、γxy和τyx、γyx分别为临界平面上的剪应力和剪应变。因此,塑性应变能包括拉伸应变能和剪切应变能两部分。
图2 减震榫内部的应力状态
通过对等强度段的有限元分析,可得出减震榫在给定榫顶水平位移u下的应力应变响应。在此基础上,通过坐标变换法可计算出疲劳损伤参数。具体求解步骤为:
(1)基于Von Mises屈服准则、多线性随动硬化准则和关联流动法则,对减震榫结构进行非线性有限元分析,确定减震榫危险位置的单元体在循环荷载作用下的应力分量σij和应变分量εij.
(2)对应力分量和应变分量进行坐标变换。通过坐标变换矩阵,不断改变坐标轴角度θ和,可以得到任意平面上的应力分量σ′ij和应变分量ε′ij.其中,θ、分别为x轴和z轴变换的角度值。
(3)根据应力分量σ′ij、应变分量ε′ij按式(1)计算任意平面上的塑性应变能,逐个对比并取其中的最大值作为疲劳损伤参量。
疲劳损伤参量的MATLAB求解流程见图3.
3.2 疲劳寿命预测
金属构件的低周疲劳具有开裂后快速疲劳失效的特点[8,9],故常用塑性应变能与疲劳寿命之间的幂指数函数关系进行疲劳寿命预测[10].减震榫在罕遇地震作用下的破坏属于低周疲劳破坏,其疲劳寿命预测公式为

式中,Nf为以循环次数计的疲劳寿命;A、β为疲劳寿命拟合的材料常数,其值可通过减震榫材料的低周疲劳试验确定。
图3 疲劳损伤参量的MATLAB求解流程

4 低周疲劳试验
4.1 试验概况
为了验证基于临界平面能量法的疲劳寿命预测方法的有效性,采用国产10号软钢制作3个减震榫试样进行低周疲劳试验。减震榫高650mm,等强度段采用圆形变截面,其截面变化规律为d (x)=15.809 4x1/3,其中150mm≤x≤650mm.
采用MTS拟动力试验系统在减震榫试样顶部施加往复循环荷载,直至发生低周疲劳失效。试样1采用逐级加载方式:首先从位移幅10mm开始循环加载,40mm以下5mm为一级,40mm以上20mm为一级,每级循环3次,直至位移幅达到140mm;然后以位移幅150mm循环加载直至试样疲劳失效。试样2和试样3加载方式相同,首先以位移幅10mm进行500次循环加载,然后以位移幅150mm循环加载直至试样疲劳失效。
4.2 试验结果分析
3个减震榫试样的低周疲劳试验结果为:试样1位移幅增加至150mm后,循环加载至7次发生疲劳失效;试样2以位移幅150mm循环加载至16次发生疲劳失效;试样3以位移幅150mm循环加载至15次发生疲劳失效。
3个减震榫试样的疲劳破坏形态(图4)基本一致:裂纹均出现在榫体等强度段的下部;疲劳损伤大部分发展于裂纹形成阶段,只有接近破坏时试样表面才出现宏观裂纹,之后裂纹迅速发展,试样断裂。
图4 减震榫疲劳破坏形态

4.3 试验结果与预测结果对比
采用临界面能量法对3个减震榫试样的疲劳寿命进行预测,首先按照图3的流程求解减震榫最大损伤面上的塑性应变能,然后根据式(2)计算减震榫在各级荷载下的疲劳寿命。其中,材料常数A、β通过对28根与减震榫试样相同材质软钢制成的试样进行轴向等幅应变的低周疲劳试验确定,根据试验结果拟合得到A、β分别为99.5、-0.58.
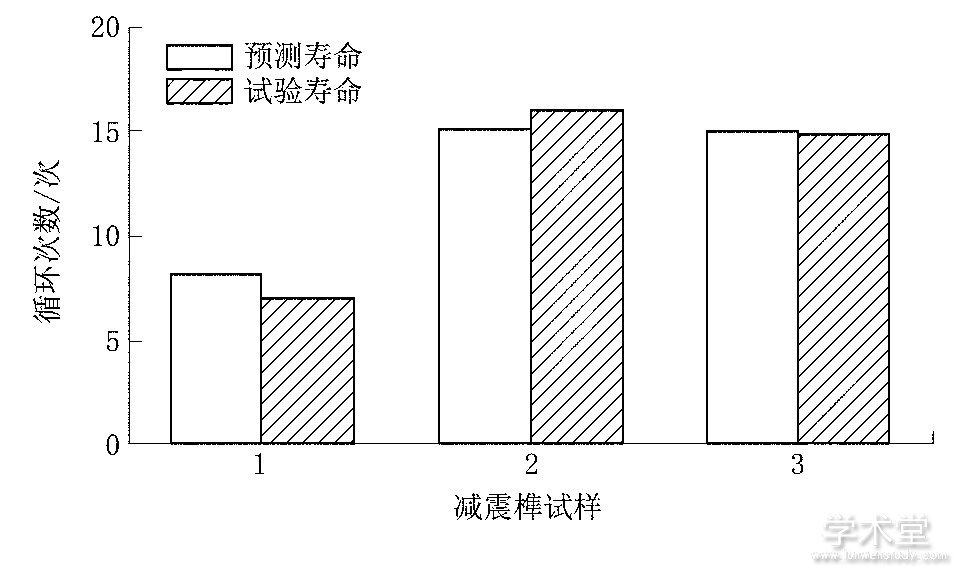
3个减震榫试样的低周疲劳预测寿命与试验寿命对比见图5.由于减震榫试样采用多级加载方式,在位移幅增加至150mm之前预测循环次数和试验循环次数相同,因此图中仅给出位移幅150mm时的循环次数。由图5可知:试样1的预测循环次数为8.1次,试样2和试样3的预测循环次数为15.08次;3个试样的低周疲劳寿命预测结果与试验结果都较为接近,试样1和试样2的预测循环次数与试验循环次数相差约1次,试样3的预测循环次数与试验循环次数基本一致。这说明采用临界面能量法进行减震榫低周疲劳寿命预测具有较好的准确性。
图5 低周疲劳预测寿命与试验寿命对比
5 结论
本文提出一种采用临界平面法和能量法组合预测减震榫低周疲劳寿命的方法,并通过3个减震榫试样的低周疲劳试验进行验证,得出以下结论:
(1) 1个试样的低周疲劳预测寿命与试验寿命一致,另外2个试样的预测寿命与试验寿命仅相差1次循环,差别较小。
(2)基于临界平面上的塑性应变能和减震榫材料的能量~疲劳寿命关系,可以较准确地预测减震榫的低周疲劳寿命。
参考文献
[1] 卢皓。罕遇地震作用下高速铁路简支梁桥抗震性能分析[J].铁道标准设计, 2015, 59 (8) :102-107. (LU Hao.Study on Seismic Performance of HighSpeed Railway Simply-Supported Girder Bridge Under Strong Earthquake Motion[J].Railway Standard Design, 2015, 59 (8) :102-107.in Chinese)
[2] 李承根, 高日。高速铁路桥梁减震技术研究[J].中国工程科学, 2009, 11 (1) :81-86. (LI Cheng-gen, GAO Ri.Study on the Shock Absorbing Technique of High-Speed Railway Bridges[J].Engineering Sciences, 2009, 11 (1) :81-86.in Chinese)
[3] 孟兮, 高日, 李承根。减震榫滞回性能理论及试验研究[J].桥梁建设, 2015, 45 (3) :20-25. (MENG Xi, GAO Ri, LI Cheng-gen.Theoretical and Experimental Study of Hysteretic Behavior of Shock Absorber[J].Bridge Construction, 2015, 45 (3) :20-25.in Chinese)
[4] 李爱丽, 高日, 李承根, 等。一种新型软钢减震榫的设计与试验研究[J].桥梁建设, 2017, 47 (1) :23-28. (LI Ai-li, GAO Ri, LI Cheng-gen, et al.Design and Experimental Study of a Novel Type of Mild Steel Shock Absorber[J].Bridge Construction, 2017, 47 (1) :23-28.in Chinese)
[5] Liu C, Gao R.Design Method for Steel Restrainer Bars on Railway Bridges Subjected to Spatially Varying Earthquakes[J].Engineering Structures, 2018, 159:198-212.
[6] Macek W, Lagoda T, Mucha N.Energy-Based Fatigue Failure Characteristics of Materials Under Random Bending Loading in Elastic-Plastic Range[J].Fatigue&Fracture Engineering Materials&Structures, 2018, 41:249-259.
[7] Branco R, Costa J D, Berto F, et al.Fatigue Life Assessment of Notched Round Bars Under Multiaxial Loading Based on the Total Strain Energy Density Approach[J].Theoretical and Applied Fracture Mechanics, 2018, 97:340-348.
[8] 鞠晓臣, 田越, 潘永杰, 等。钢桥贯通疲劳裂纹扩展行为预测方法研究[J].桥梁建设, 2015, 45 (2) :53-57. (JU Xiao-chen, TIAN Yue, PAN Yong-jie, et al.Study of Prediction Methods for Propagation Behavior of Through Fatigue Cracks in Steel Bridge[J].Bridge Construction, 2015, 45 (2) :53-57.in Chinese)
[9] 许金泉。疲劳力学[M].北京:科学出版社, 2018. (XU Jin-quan.Mechanics of Fatigue[M].Beijing:Science Press, 2018.in Chinese)
[10] Sarkar P P, De P S, Dhua S K, et al.Strain Energy Based Low Cycle Fatigue Damage Analysis in a Plain C-Mn Rail Steel[J].Materials Science&Engineering A, 2017, 707:125-135.