地表季节性形变的已知物理成因与阐释

　　摘    要：　地表形变运动的成因探索对环境监测、气候变化研究以及高精度地球参考框架维持都具有重要意义,主要讨论了地球表面非构造季节性运动的物理因素。首先介绍了两个已经明确了的激发机制：由大气、海洋、陆地水、雪、冰以及植被等变化引起的表面质量重力负荷,是地表季节性形变的主要激发源,可以解释40%50%的垂向和15%20%的水平向地表季节性形变；除此之外,地表温度变化引起的热弹性形变对GPS台站观测到的周年位移也存在激发作用,在垂向和水平方向的贡献率分别为7%和8%9%。其次探讨了地表三维季节性形变的潜在物理机制,现有的理论证明和区域性的观测结果均表明,由地下水含量变化引起的孔隙弹性负荷极有可能对地表形变存在贡献。孔隙弹性形变的情况不同于传统水文负荷,却与热弹性效应类似,可以通过改进现有的热弹性形变模型,并将其应用到陆地水系统,拓展出全球尺度的孔隙弹性形变模型,进一步补充解释地表三维(尤其是横向分量)季节性形变。

　　关键词：　地球参考框架; 物质重力负荷; 热弹性形变; 孔隙弹性形变;

　　Abstract：　The causes exploration of surface deformation is greatly significant to environmental monitoring, the study of climate change and maintaining of high precision terrestrial reference frame. This paper mainly summarize physical causes of those non-techtontic 3D surface deformation. Firstly, by comparison between the observation and predictions based on geophysical modeling, we find that on average 50% vertical and 20% horizontal displacements(amplitude and phase) of the GPS stations, can be explained by surface mass loading from the atmosphere, ocean, ground water, snow, glaciers, canopy, etc. And the latest work shows that the thermal expansion deformation contribute 7% to the annual GPS displacements in vertical and 8%9% in horizontal direction, respectively. Then the potential physical mechanism of 3D seasonal surface deformation is discussed. Although the accuracy of thermoelastic deformation estimation can be enhanced by a more realistic thermoelastic deformation model, the improvement is unlikely dramatic. Some additional physical mechanisms must be involved in producing the surface deformations. As part of future work, we discuss in perspective the extension of the thermoelastic model to poroelastic deformation to include the terrestrial water system into the cause of the 3D surface deformation.

　　Keyword：　Terrestrial reference frame; mass-loading effect; thermoelastic deformation; poroelastic deformation;

　　1 、引言

　　全球GPS网(International GNSS Service,IGS)可以监测地心移动(包括大气、海洋的整体地球质心相对于固体地球的形状中心的运动)和固体地球旋转运动，是维持高精度地球参考框架的重要手段。同时IGS台站的坐标变化直观地反映了地球表面的构造运动和形变运动，在季节变化的时间尺度下，台站坐标变化机制不属于构造运动。它的激发机制涉及到地球表面各种物质的大尺度季节性移动和重新分布，也联系了地壳对非物质重力负荷的地球物理场(如温度场和磁场)季节性变化的响应。当前，全球GPS网正进入一个亚毫米精度的新时代。同时，卫星重力测量(Gravity Recovery and Climate Experiment,GRACE)和合成孔径雷达干涉系统(Interferometric synthetic aperture radar,INSAR)也在具体实施下一代的设备和观测。在这些新测量技术发展的同时，相应的模型建立也面临着挑战：在全球范围内许多细小的物理因素将不容忽视。因此，需要拓展现有研究范围，对一些细小的物理机制进行探索(如热弹性和孔隙弹性形变等)。

　　现有研究表明，在剔除线性趋势、构造相关信号和明显的局部效应后，GPS台站位置时间序列中存在普遍的季节性信号[1,2,3]。GPS台站位移序列中的季节性信号主要为周年变化，其中垂直(径向)分量的幅度为5?20 mm；水平(横向)分量较小，约2 mm。受区域性因素影响，在这些GPS台站中也有一些例外的特别显着的周年形变，主要存在于极端天气和地形条件下，如亚马逊河流、阿拉斯加、喜马拉雅山和极度干旱地区[4,5,6]。简洁起见，以下与GPS台站位移有关的垂直或径向和水平或横向指的是那些非构造运动的周年信号。
 

　　近年来，许多学者针对单个或多个地表物质的重力负荷效应，分别从区域小尺度和全球大尺度范围内，开展了关于IGS网垂直和水平位移季节性变化的研究[7,8,9,10,11,12,13,14,15,16,17,18]。综合这些研究结果表明，约50%的IGS网垂直位移可以用大气、海洋、陆地水(地表水和地下水)、雪、冰(冰川和冰盖)以及植被等变化引起的表面质量重力负荷(以下简称物质重力负荷)来解释；同时，物质重力负荷对水平位移的贡献情况则有很大的不同，相同的荷载模型只占IGS网水平位移的20%。物质重力负荷形变的结果主要通过两种手段来实现，一是根据美国航空航天局(National Aeronautics and Space Administration,NASA)和美国国家气象局(National Oceanic and Atmospheric Administration,NOAA)等汇编的数据，结合物理模型进行计算；二是通过GRACE观测的重力数据进行载荷反演。在全球大部分地区，两种手段获取的物质重力负荷形变结果吻合较好，在少数地区由于区域因素以及模型误差等差别较大。

　　另一种可能导致地球表面位移的机制是热弹性形变。关于热弹性形变的研究相对较少，1975年Berger[19]提出第一个半无限空间上的热弹性形变模型；1986年Ben-Zion和Leary[20]对该模型进行扩展，然后建立一个弹性解耦层半无限空间模型。此后，一些学者运用该模型估计地表温度变化引起的热膨胀效应，及其对GPS台站径向位移的影响[1,21,22]。2014年Fang等人[23,24]提出一个有限球形空间热弹性形变模型，首次在全球范围内计算了包括径向和横向分量的三维地表热弹性形变。2017年Xu等人[25]以及谭伟杰等人[26]的研究工作表明，热膨胀效应对GPS(GNSS)台站周年位移的贡献率在垂向和水平方向分别为7%和8%?9%。

　　目前，在全球尺度下关于地表季节性形变的研究，绝大部分都是基于物质重力载荷引起的形变，关于非物质重力负荷部分的研究比较少。对地表季节性变化的物理成因可以主要从提高区域性物质重力负荷效应的计算精度和增加对非物质重力负荷的影响研究展开。其中关于非物质重力负荷的研究可以分为两部分：一是目前的三维热弹性模型比较粗糙，需要进一步改进到接近地球的真实状态，来提高对热弹性效应的计算；其次是将热弹性形变机制延伸至地下水量变化引起的孔隙弹性形变，在全球范围内评估其对IGS位移(尤其是水平方向)的影响。

　　第2章将主要介绍地表三维位移季节性形变的已知激发因素(物质重力负荷和热弹性形变)；第3章将对地表季节性形变的潜在因素(孔隙弹性形变)进行探讨；第4章是对全文的总结以及对未来研究工作的展望。

　　2 、地表季节性形变的已知物理成因

　　近几十年来，随着空间观测技术的提高和大气、海洋、地下水等地球物理资料的丰富，我们能够更深入地认识和研究地表位移形变，揭示其运动规律。已有研究表明，约50%的垂直位移和20%的水平位移可以用地表质量变化引起的物质重力负荷效应来解释；其次，约7%的垂直位移和9%的水平位移可以用地表温度变化引起的热膨胀效应来解释。

　　2.1 、物质重力负荷效应

　　大气、海洋、地表水(湖泊、河流、水库)、地下水(土壤含水层及底下的地下蓄水层)、积雪、冰盖(南极和格陵兰岛)、大陆冰川以及植被等地球表面物质分布会随着时间变化，而这些物质对地壳压力负荷的变化会引起地壳的变形。由物质重力负荷引起的地表三维形变中，周年变化最显着，且各分量变化在垂直方向尤为明显，最大可达十几毫米。

　　为了明确各种物质对地表形变的具体贡献，表1列出了不同重力负荷源名称及其常用物理模型。同时，剔除一些异常数据，并均匀挑选出230个GPS台站，分别统计了垂向、水平南北以及东西向不同重力负荷源对总物质负荷的平均占比。可以看出，这些地表物质中，大气负荷效应最显着，对总物质重力负荷的平均占比分别为39%(垂向)、45%(南北向)、44%(东西向)；海洋负荷次之，为23%?29%；土壤湿度、雪、植被等其他因素单个负荷效应比较小，合起来的平均占比分别为35%(垂向)、32%(南北向)和27%(东西向)。

　　表1 不同重力负荷源及其模型以及对总物质重力负荷形变的平均占比

　　结合GPS、GRACE观测数据以及各种大气、海洋和水文等资料模型，许多学者先后对地表质量重力负荷效应进行了广泛的研究[16,25,26,27,28]，分析不同手段获取的物质重力负荷形变及其对地表周年形变的贡献，得出了类似的结论：一方面，GPS观测的周年三维位移比另外两种手段获取的位移显着，尤其是在水平方向；这主要是因为GPS台站位移包含了区域性的物质重力负荷因素和非物质重力负荷因素的影响，因此会比单独的物质重力负荷形变更明显。另外两种手段(GRACE观测和模型计算)获取的三维周年位移在绝大部分台站上均符合较好，少量近海台站的两种负荷形变存在明显的振幅和相位差别；这主要是因为GRACE观测和负荷模型反映的都是大尺度的物质迁移效应，因此两种模型平均符合较好，局部地区由于特殊条件存在较大差异。另一方面，物质重力负荷形变对GPS台站观测的周年位移在垂向上有显着贡献，约为50%；在水平方向上的贡献没有垂向上明显，约为20%。这一结果主要是由于重力表面的质量载荷横向分量比较小，约占径向分量的10%，因此物质重力负荷的横向形变不能对IGS网的水平位移进行充分的解释[24]。

　　对地表物质重力负荷效应的估计主要通过GRACE观测数据反演和地球物理模型估算的负荷形变来实现，但是这两种手段仍然存在缺陷。首先，由于GRACE反映的是大尺度的质量迁移，对区域性小尺度物质源(如深层地下水)的影响缺乏空间分辨率；另外，GRACE资料的反演是基于所有质量变化为地表负荷的前提进行的，而来自地下的负荷产生的形变恰恰与地表负荷形变的方向相反，因此在地下负荷主导的区域GRACE资料反演的形变结果会出现很大偏差[14]。而地球物理模型反演也存在很多不足，如大陆冰川观测数据密度不够(每年只有一个，无法估计周年变化)、冰盖数据空间覆盖不全、以及全球的地下水资料缺乏(如深层地下水)等。因此，GRACE观测数据和地球物理物质重力负荷模型估计的负荷效应均存在一定的误差。与此同时，尽管物质重力负荷效应对GPS三维周年位移贡献很多，但垂向和水平向的物质重力负荷贡献率存在较大差异，这表明，即使重力负荷模型进一步优化，与垂直分量相比，IGS网观测到的水平位移仍然有很大一部分无法解释，除地表质量荷载效应外，还需要探索其他非物质重力负荷物理机制。

　　2.2 、热弹性形变

　　太阳通过核聚变反应源源不断地释放出大量的能量，然后以电磁辐射的方式传递至地球，从而加热地球表面。由于地球相对太阳存在公转运动，地表温度呈现显着的周年变化，这种变化引起的热弹性形变也能激发地表的季节性形变。热弹性理论是在20世纪因为工程和材料科学发展而提出来的[29]。在地球科学中，1975年Berger[19]首先提出了二维均匀半无限空间上的热弹性应形变模型；1986年Ben-Zion和Leary[20]对该模型进行扩展，给出了与深度相关的水平热弹性形变模型，但仍然是二维模型。前面两种模型中的热弹性形变存在于一个由太阳辐射驱动的半无限空间中，可以看作是将一些平面贴片机械地粘接在地球表面上，这些有限大小的贴片相互不影响，不能估计横向热膨胀效应，对径向分量的估计也不够充分；此外，半无限空间热弹性模型没有对地球质量中心的运动进行任何限制[30]，存在很大的局限性。由于地球实际是球形的，如果在地球表面上有一个水平方向的温度梯度，则必然在地球表面的反方向也存在着水平温度梯度，因此，必须计算来自各个方向的温度梯度造成的热弹性形变才能得到准确的结果。基于此，2014年Fang等人[23]在地心保持静止的约束条件下，将半无限空间解扩展到有限体积的均匀弹性球体，发展出了球空间热弹性形变模型，首次在全球范围内估计了地表三维热弹性形变。

　　为了更加清晰地认识热弹性理论的发展历程，表2列举了几种热弹性形变模型中使用的热传导方程及其主要特点。其中，Berger的半无限空间模型仅考虑由静止波给出的局部表面温度场，在热传导方程中，T为温度，x为距离，t为时间，T0为初始温度幅度，ω为频率，κ为热扩散系数；Ben-Zion和Leary的弹性解耦层半无限空间模型引入深度参数，考虑了弹性半无限空间内的二维温度分布，Tω为初始温度幅度，?为初始相位，y为深度参数，γ为热扩散参数；Fang等人的全空间热弹性形变模型则考虑了包括远场在内的各个方向的热弹性应力，r为地球半径，θ,φ分别表示余纬和经度，η为热扩散系数。

　　表2 不同热弹性形变模型的原理特点

　　2017年Xu等人[25]基于此三维热弹性形变模型，采用NOAA的地表温度数据，计算了由热膨胀效应引起的地表三维周年形变位移。结果表明，热弹性形变在垂向上的最大振幅约为3 mm，在水平方向上约为1.5 mm。同时，针对选定的230个IGS站点，结合热弹性形变以及物质重力负荷形变，与观测到的IGS测站位移进行了一系列的对比分析。该项工作选取了三个研究方案：(1)单独的物质重力负荷模型；(2)物质重力负荷模型加上半无限空间热弹性形变模型；(3)物质重力负荷模型加上热弹性模型。结果显示，从方案(1)到(3)，垂直和水平方向上的位移对比符合度逐步增大。其中，尤其值得注意的是，叠加热弹性模型后在垂直和水平位移上的改进大致相等(在垂向和水平方向分别增加了7%和8%?9%)。以上对比结果揭示了3个方面的问题：(1)证明了全空间热弹性模型比半无限空间模型具有优越性；(2)热弹性模型得到的水平方向位移约为垂直方向的50%，但对IGS位移在水平和垂直方向的贡献率大致相等，相比之下，物质重力负荷引起的水平位移仅占垂直位移的10%，对IGS位移的贡献率也仅是垂直方向的1/3;(3)由于热弹性模型得到的形变远小于物质重力负荷形变，因此热弹性模型对IGS网水平向位移的改善显得特别突出。

　　全空间热弹性形变模型首次估计了地表三维热弹性形变，与物质重力负荷形变相比，很大程度上增加了对IGS网水平位移的解释。然而实际上，太阳辐射引起的热量变化穿透地球表面以下约3 m[19,30]，现有模型统一归算到地球表面来估计热弹性形变，结果还存在一些误差。未来可以将这个初始模型扩展到一个自引力的、完全分层的现实地球状态，以提高对热弹性效应的估计精度。

　　3、 地表季节性形变的进一步解释

　　Xu等人2017年通过研究得到一个结论：地表物质质量载荷的横向分量约占其径向分量的10%，而热弹性载荷的横向分量约为其垂直分量的50%[25]。这种差异性表明，还有其他类似于热弹性形变的机制可以产生足够的水平形变来解释观测到的IGS横向位移，而又不会产生特别大的垂向形变从而过度解释径向位移，这个机制就是孔隙弹性形变。以上结论已被Fang等人[24]2014年从理论上进行了证明；Tan等人[14]2016年以加利福尼亚州中部山谷地区的数个IGS台站为例，也对该结论进行了观测上的证实。Tan等人重点分析了GPS观测位移和GRACE资料反演的质量载荷两者之间的差异，结果表明，在地下水抽取严重的地方，GPS台站位移与GRACE反演的载荷间不一致性较大，结合当地水井资料，证实两者之间的差异与地下水含量变化所引起的孔隙弹性载荷密切相关。总之，目前关于孔隙弹性荷载在全球尺度上的研究还比较少，以下主要从孔隙弹性荷载的定义及其与传统水文的区别，以及其中存在的两种相反效应(质量载荷和孔隙压力载荷)，半定量地论述其对地表季节性形变的激发。

　　3.1、 孔隙弹性荷载

　　所谓孔隙弹性荷载，是指含水层和基岩中因含水量的变化而产生的一种特殊载荷。孔隙弹性荷载与传统水文负荷不同，传统的水文负荷问题涉及到通过抽水来降低孔隙压力，从而使含水层骨架从上覆体的荷载中压缩，并导致地面沉降，这里的荷载是全部的地表质量加上含水量。而在孔隙弹性荷载问题中，承压含水层上方含水量的变化是主要的载荷来源。

　　两种荷载机制的差异也可以从大地测量信号中看出，其中有两个重要的特征。第一，抽水导致地面沉降是一个长期的趋势过程，而上覆蓄水量变化引起的孔隙弹性荷载具有很强的季节性。第二，与抽水有关的大地测量信号往往相互加强。例如，抽水耗水会降低重力信号，地面沉降也会降低重力信号；孔隙弹性负荷的情况则不同：蓄水量的增加使地面受到其重量的抑制，同时，随着储水量的增加，孔隙压力的增加将扩大含水层的体积，驱动地表的隆起。

　　3.2 、孔隙弹性荷载的相反效应

　　孔隙弹性载荷包含两个部分：质量载荷和孔隙压力载荷，两者都是由承压含水层上储水量的变化引起的。为了证明这两种机制是相互抵消的，这里采用NOAA的全球土壤水分含量的6 h时间序列得出了季节性水位信号ω，用球谐展开可以写成：

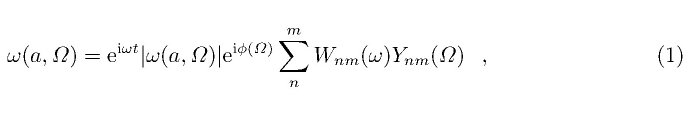
　　其中，a为地球半径，ω为频率，?表示位置(余纬θ和经度φ)，?(?)为相位函数，Wnm是周期性表面载荷的复谐波系数，Ynm为Legendre多项式。虽然土壤层可能不够深，无法容纳GRACE所检测到的整个地表水再分布，但可以合理地假定复杂完整的时空分布数据可以模拟真实的地表质量变化。在已知荷载勒夫数的情况下，用式(2)可以计算水质量载荷引起的垂直和水平形变[29,31]。

　　式中，ur表示垂直形变，uL表示水平形变，ρw为水密度，ρE为地球平均密度，hn为垂向载荷勒夫数，ln为横向载荷勒夫数。

　　根据热膨胀与孔隙压力膨胀的相似性，用Fang等人[23,24]的热弹性形变模型，将温度Tnm替换为水压gρwWm，热扩散率η替换为水扩散率ηp，热膨胀系数β替换为孔隙膨胀系数βp/3，可以计算由于相同的上覆储水变化引起的孔隙压力垂直和水平形变。

　　这里，为了比较，我们将孔隙压力与质量载荷的共同因素等同起来，采用式(3)对孔隙压力载荷进行归一化处理：

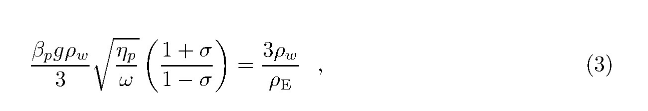
　　式中，σ为泊松比，然后均匀挑选全球230个GPS站点，并给出计算对比结果(见图1)。其中，蓝色箭头表示水量变化引起的质量重力负荷，红色箭头表示孔隙压力载荷，箭头的长度和方向分别表示标准化的年振幅和相位，相位由正弦约定：sin(ωtφ)定义，t为起始年，从东逆时针方向绘制。

　　图1 230个IGS站点因水量变化引起的归一化质量重力负荷(蓝色)和孔隙压力负荷(红色)对比图

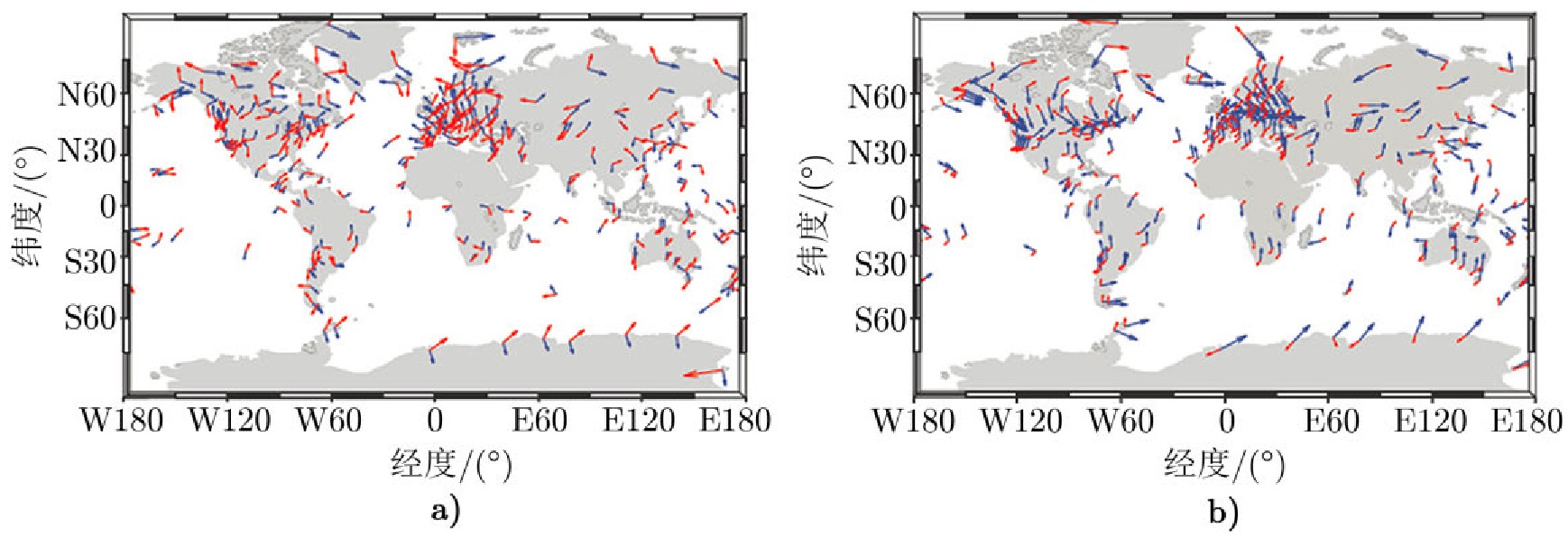
　　注：a)垂直分量；b)水平南北分量。

　　图1给出了孔隙弹性荷载中质量载荷和孔隙压力载荷的对比，孔隙压力在承压含水层中的扩散引起了压力载荷的45?相位延迟[23]，而图中所示的相位差一般远大于45?，表明了两种载荷强烈的相反效应。简单描述就是：随着地下水质量增加，孔隙压力负荷使得地面上的弹性地壳上升，同时质量重力负荷使得下面的地壳(连带上面的地壳)下沉，两种效应同时存在并作用。由图1可知，两种相反机制的抵消减少了孔弹性载荷对大地测量信号的影响，但是这样的系统更难建模。

　　孔隙弹性负荷的情况不同于传统水文负荷，却与热弹性效应类似，因此可以将热弹性形变模型扩展应用到孔隙弹性形变。但是，尽管两者在数学公式上有一些共同之处，水文系统却比辐射加热系统要复杂得多。现有研究一直把水文参数当作全局常数，这与现实不符，未来可以采用机器学习方法[32]来计算水文参数，量化与质量载荷相关的相反影响，以期进一步解释地表季节性横向和径向形变。

　　4、 结论与展望

　　现有的空间大地测量技术(GPS,GRACE,INSAR等)提供了高精度和高时间分辨率的观测数据，结合气象学、海洋学、地震地质学等多学科的知识和地球物理资料，人们对地表下季节性运动的研究有了非常广泛和深入的发展。地表季节性变化研究一方面揭示了地表大规模物质迁移的规律，另一方面对维持高精度地球参考框架具有重要意义。然而，关于IGS网观测到的地表下非构造季节性运动的全部激发因素距离完全探明还有很大的差距。目前的研究结果表明，物质重力负荷是比较明确的物理因素，它激发了50%左右的地表季节性垂向位移和20%左右的水平向位移；此外，地表温度变化引起的热弹性效应也有贡献，在垂向和水平方向分别为7%和8%?9%。由温度变化引起的地表位移已经足够大(特别是在水平方向)，在高精度的地球参考框架维持中必须予以考虑。

　　当前，关于物质重力负荷引起的地表周年形变的研究比较多，而关于非物质重力负荷影响的研究相对较少。除去已经明确的大尺度物质重力负荷、全球热弹性效应，以及模型误差等，还有大约30%和60%的径向和横向位移激发因素没有确定。未来研究可以从两方面着手：(1)区域物质重力负荷效应。随着后续GRACE-Follow-On和GRACE-II计划的开展，能够获取越来越多高精度和高分辨率的地球物理数据(如大陆冰川、冰盖、地表水和地下蓄水层)，可以更深入地研究区域性小尺度物质重力负荷效应的影响。(2)非物质重力负荷效应。一方面可以对现有的热弹性形变模型进行改进，扩展到一个接近真实情况的地球模型；另一方面将改进的热弹性模型应用到孔隙弹性效应，然后结合地下水资料，并采用机器学习方法估计水文参数，在全球尺度上评估孔隙弹性形变对地表下季节性运动的贡献。

　　参考文献

　　[1] Dong D N,Fang P,Bock Y,et al.JGR,2002,107:5
　　[2] Tsai V C.JGR,2011,116:B04404
　　[3] Van Dam T,Wahr J,Lavalle′e D.JGR,2007,112:B03404
　　[4] Marengo J A,Espinoza J C.International Journal of Climatology,2016,36:1033
　　[5] Chanard K,Avouac J P,Ramillien G,et al.JGR,2013,119:5097
　　[6] Bevis M,Alsdorf D,Kendrick E,et al.Geophys Res Lett,2005,32:L16308
　　[7] Fok H S,Liu Y X.Remote Sensing,2019,11:1433
　　[8] Liu Y X,Fok H S,Tenzer R,et al.Entropy,2019,21:664
　　[9] Wang S Y,Chen J L,Wilson C R,et al.Geophys J Int,2018,212:1302
　　[10] Zhang W,Li F,Hao W F,et al.Geophys J Int,2017,210:1295
　　[11] Liu L,Khan S A,Van Dam T,et al.JGR,2017,122:677
　　[12] Gu Y,Yuan L,Fan D,et al.Adv Space Res,2017,59:88
　　[13] Li W,Van Dam T,Li Z,et al.Studia Geophysica et Geodaetica,2016,60:608
　　[14] Tan W J,Dong D N,Chen J P,et al.Advances in Space Research,2016,57:19
　　[15] Demir D O,Dogan U.Advances in Space Research,2014,53:458
　　[16]魏娜,施闯,刘经南.地球物理学报,2015,09:3080
　　[17]姜卫平,夏传义,李昭,等.测绘学报,2014,43:1217
　　[18]杨元德,鄂栋臣,晁定波,等.地球物理学报,2009,52:2997
　　[19] Berger J.JGR,1975,80:274
　　[20] Ben-Zion Y,Leary P.Bull seism Soc Am,1986,76:1447
　　[21] Yan H M,Chen W,Zhu Y Z,et al.Geophys Res Lett,2009,36:L13301
　　[22]Richey A S,Thomas B F,Lo M H,et al.Water Resou Res,2015,51:5217
　　[23] Fang M,Dong D N,Hager B H.Geophys J Int,2014,196:194
　　[24] Fang M,Hager B H,Dong D N.J Surveying and Mapping,2014,89:4
　　[25]Xu X Q,Dong D N,Fang M,et al.GPS Solutions,2017,21:1265
　　[26]谭伟杰,许雪晴,董大南,等.测绘学报,2017,46:1080
　　[27]Ray J,Altamimi Z,Collilieux X,et al.GPS Solut,2008,12:55
　　[28] Yan H M,Chen W,Yuan L G.Geophys J Int,2016,204:505
　　[29] Biot M A.J appl Phys,1956,27:240
　　[30] Hill E M,Davis J L,Elosegui P,et al.JGR,2009,114:B11402
　　[31] Rice J R,Cleary M P.Rev Geophys Space Phys,1976,14:227
　　[32]Beck J L,Au S K.J Eng Mech,2002,128:380