摘 要: 太阳活动作为影响地球气候和地表环境变化的驱动因素.根据太阳黑子观测数据和磁性变化特征构建太阳黑子磁场磁性指数时间序列MI,基于索周法来研究其周期性变化规律.通过与算术平均周期法、傅里叶分析方法和Morlet小波分析方法的比较,发现利用索周法处理近270年太阳黑子磁极性数据,可以得到显着的22.25年的周期性规律.利用索周法得到的周期数值与谱分析方法探求结果相吻合.在寻求周期性规律方面,索周法可有效避免程序算法过程中存在准确分解信号、分辨率低、基函数选择等缺点;根据数据分析的计算需要,具有缩小误差范围、提高精度的可控优势.这一研究方法与主流的谱分析相辅相成发展,能有效覆盖多种周期的检测,为探究太阳运动及太阳活动周期性规律提供参考依据,进而为深入研究全球气候、地表环境变化开辟新的思路.
关键词: 太阳黑子磁性数; 索周法; 22.25年周期; 全球气候变化; 周期性规律;
Abstract: Solar activity as a driving factor affecting changes in the earth's climate and surface environment. According to the observation data of sunspots and the characteristics of magnetic change, the magnetic index MI of the solar magnetic field is constructed, and the periodic change rule is studied based on the cycle exploring method. Comparing with Arithmetic mean period method, Fourier analysis method and Morlet wavelet analysis method, it is found that using the cycle exploring method to process the magnetic polarity data of the sunspots for nearly 270 years can obtain a significant 22.25 years periodic rhythm. The cycle value obtained by the cycle exploring method is consistent with the search result of the spectral analysis method. In the search for periodic laws, the cycle exploring method can effectively avoid the shortcomings of accurate signal decomposition, low resolution, and selection of basis functions in the process of program algorithms; according to the calculation needs of data analysis, it has the controllable advantages of narrowing the error range and improving accuracy. This research method complements and develops with mainstream spectral analysis, and can effectively cover multiple periods of detection, provide a reference for exploring the periodic laws of solar motion and solar activity, and then open up new ideas for in-depth study of global climate and surface environment changes.
Keyword: Sunspot magnetic number; The cycle exploring method; 22.25-years cycle; Global climate change; Periodic law;
0 、引 言
当前关于太阳活动22年周期的成因探讨,仍是争论激烈、尚存争议的热点话题(Jose,1965).相关研究表明,太阳活动具有特定的周期性,太阳磁场变化具有显着的22年周期性韵律(Babcock,1961;Tlatov,2007).太阳活动作为不可或缺的天文驱动因子,逐渐成为联系全球气候变化机制分析的关注焦点,对深入研究全球气候及地表环境周期性变化具有重要意义;其中,学者赵佩章等(2001)、左小敏和万卫星(2002)就太阳活动驱动海洋异常变化、影响电离层扰动等研究取得可喜成果.继天文物理学家发现约11 a的Schwabe周期、约22 a的Hale周期、约210 a的Suess周期等不同尺度的太阳活动周期后(Schwabe,1843;Hale and Seth,1938;Suess,1980);为表征太阳黑子活动的强弱程度,Wolf首次提出太阳黑子相对数的概念即沃尔夫黑子相对数,并成功测算出太阳黑子具有平均11.1年的周期成分(唐洁和刘晓琴,2018).太阳黑子相对数作为表征太阳活动强弱的指标,对于探究太阳活动凸显的特殊作用和指导价值,已成广泛共识;为此,多渠道地观测和记录太阳活动,尝试收集不同时段太阳黑子数据用于探析太阳活动规律.目前学术界普遍接受的观点认为,太阳黑子活动具有准11年周期性韵律(Hood and Jirikowic,1991;占腊生等,2006;李可军等,2010),太阳活动所蕴含的22年磁周期韵律称之为Hale周期(Charvátová,2000;曲维政等,2007;Krivova et al.,2010).例如:Hood和Jirikowic(1991)、Charvátová(2000)研究表明,太阳运动和太阳活动存在显着周期性特征;杨冬红和杨学祥(2013)也研究获取了太阳黑子具有准11年周期性韵律;曲维政等(2007)通过构建太阳黑子磁场极性指数的特征函数,分析发现太阳磁场极性存在强烈的22年周期.刘复刚等(2013)利用行星系质心绕日运转简化模型,数值模拟得到行星系质心的平均绕转韵律也显着呈现出22年周期;同样,孙威等(2017,2017)为准确标定任意时刻绕转天体质心的精确位置,进而提出日心经度指标方程,可精确描绘出天体系统内互相关联的绕转系统质心运转轨迹,显示出具有11.5年的周期性,为诠释指标方程关联要素之间的内因联系做出贡献.另外,太阳活动周期性变化引发的全球气候变化及地表环境演化被广泛关注(Suess,1980;Sonett and Finney,1990).学者吴姗薇等(2014)利用太阳黑子磁场极性指数,结合SLP和NCEP/NCAR归一化处理,并通过小波分析计算发现,太阳磁场极性指数时间序列与东亚夏季风存在相对一致性的22年和40年双尺度周期规律;杨春霞等(2011)采用经验模态分析,发现南京市和石家庄市在短中时间尺度的气温变化规律中存在类似于太阳黑子的准11年周期成分;赵新华和冯学尚(2014)借助相关记录及TSI重构数据,采用交叉小波分析途径,获取世纪时间尺度下太阳活动与地表温度变化的关系,结果显示全球气温变化也存在与太阳活动相同的22年周期.与此同时,关于全球气候及地表环境变化驱动力成因一直众说纷纭,针对冰川、海洋、湖泊、树木年轮中相关沉积物或核素的定性研究,同样发现两者存在基本一致的同尺度周期特征.

本文通过索周法对近300年来观测记载的太阳黑子磁场极性数据进行周期规律探求,参照功率谱估计和Morlet小波分析的结果作对比研究,寻求与不同类型的周期性研究方法之间相辅相成发展,为后期准确建立太阳黑子磁场磁性指数时间序列奠定重要基础,最终为太阳活动可能引发的自然灾害评估与预测、空间环境监测等前瞻性研究提供理论依据.
1 、太阳黑子磁极性周期的探求及分析
1.1、 太阳黑子磁极性指数
根据苏黎世天文台记载的太阳黑子数据,结合太阳黑子磁性变化规律特征,曲维政等(2008)采用数学方法,为研究太阳黑子磁场极性指数变化与地球物理事件的相关性,确立相对数曲线序列指标——太阳黑子磁场极性指数MI.借此基础,针对太阳黑子磁场磁性指数构建特点,利用美国航空航天局(NASA)观测的太阳黑子数据资料,重新构建太阳黑子磁场磁性指数时间序列(Sunspot Magnetic Field Polarity Index,SMFPI).SMFPI的建立有助于地学研究者从太阳磁场变化的角度,思考和研究太阳活动对地表环境及诸多地球物理事件的影响方式和作用途径.因此,准确分析太阳黑子磁场极性指数的周期性韵律,对于梳理出因太阳磁场变化引发的太阳运动及太阳活动,在驱动全球气候环境变化、引发地表环境演变等事件周期的关联表现中,具有极为重要的借鉴意义和理论价值.
图1为太阳黑子磁场磁性指数时间序列(SMFPI)在1749—2019年的相对数曲线,通过交叉划分形式区划出涵盖不同奇数个周期(5个、9个、11个)、偶数个周期(6个)的时域区段.其中,t1=(M2-M1)/11=21.82年、t2=(M4-M3)/9=22.45年、t3=(M6-M5)/6=21.81年、t4=(M8-M7)/5=22.06年.为此,取算术平均周期作为太阳黑子磁场极性变化的平均周期长度即T=(t1+t2+t3+t4)/4=22.04年.
图1 太阳黑子磁场极性指数周期划分图
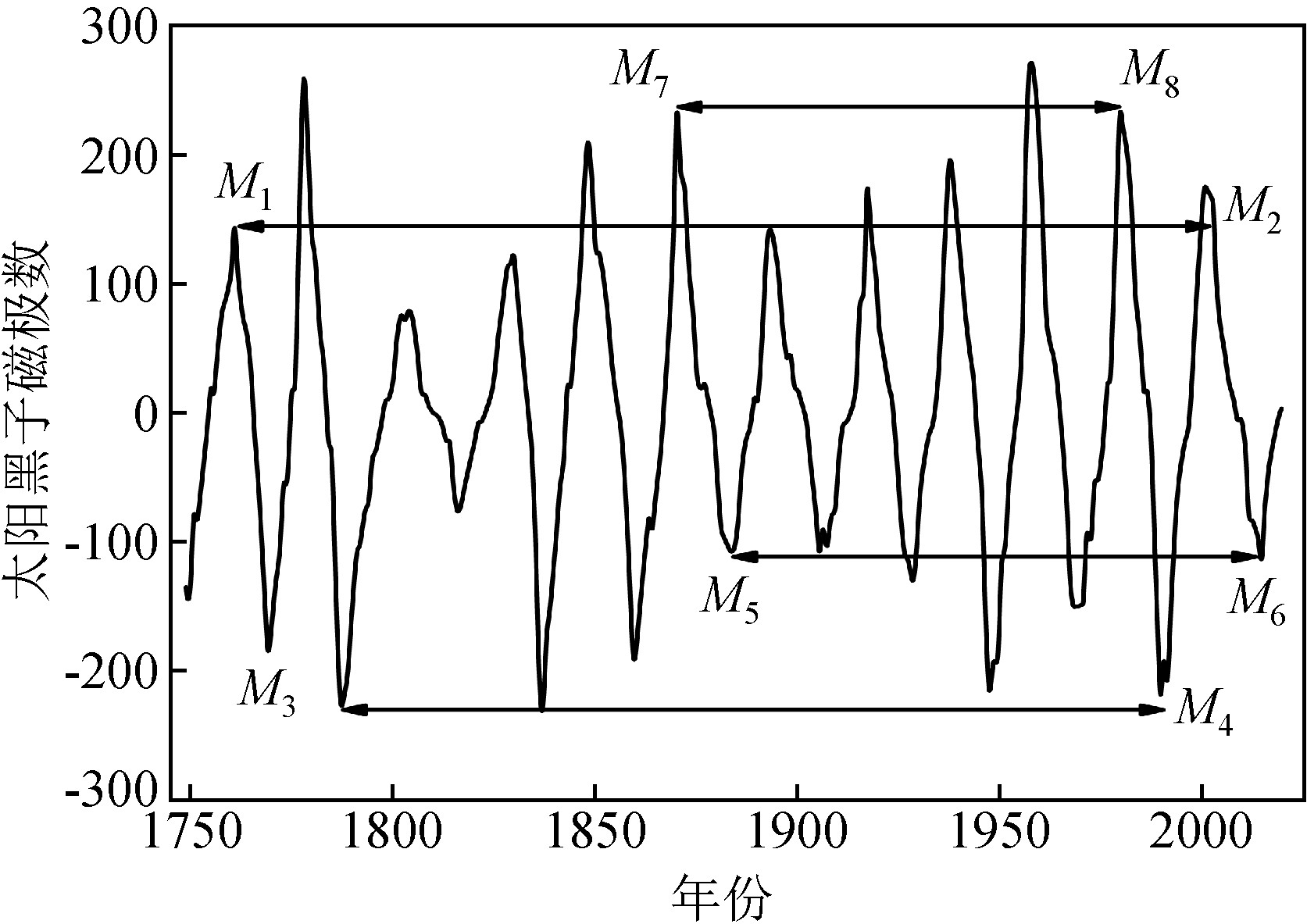
Fig.1 Period pision diagram of the polarity index of the sunspot magnetic field
平均周期法针对时域区段划分和区间长度的计算,存在一定的人为因素,涉及周期区段的选择和计算均会产生相应的随机误差.利用算术平均周期代替实际平均周期,其精度较低并且对固有误差的消除存在不同程度的困难.因此,寻找合理、准确的周期探求方法对于研究太阳黑子磁场极性指数的周期韵律至关重要.本文将从多角度揭示太阳黑子磁场极性指数变化的多尺度周期规律,进而为深刻研究诱导全球气候和地表环境变化的天文因子奠定基础.
1.2、 太阳黑子磁极性周期探求
索周法是通过数据处理、分析其变化特征,而获得相关数据变化规律的一种周期性分析方法.该方法处理的基本流程是按照不同类型排列矩阵并对矩阵中各列的数值求和,利用各数值之差的绝对值大小反映数据变化的显隐性.因此,将蕴含周期性规律的数据反映在不同行数或列数的系列矩阵中,对各矩阵不同列的数值求和,利用各求和数值之差的绝对值(|ΔF(t)|)反映在以矩阵列数代表周期的曲线中,即曲线中的波峰或波谷坐标值(Whittaker and Robinson,1944).这一数据处理方法在探求数据隐含的短、中尺度的周期性规律,具有良好的优势;若结合计算机协同处理,能较完整地覆盖长周期韵律探求的需求.陈彪和印春霖(1965)利用1750年以后210年的太阳黑子相对数,对月平滑平均值进行索周处理,得到太阳黑子磁场极性数据的主、次周期;改进了Anderson C.等仅发现其主周期而创建的周期函数曲线表达式,成功建构出相对数曲线的近似描述方程.本文借助太阳黑子磁场极性指数最新数据,利用索周法探求其变化的周期性韵律,优化各处理步骤和方案,得到相对完整、准确的周期,为后期构建准确的太阳磁场极性指数时间序列预测方程奠定基础.
索周法的具体步骤:
(1)将太阳黑子磁场极性基础数据以时间步长为1年,从1755年为起点确定相对数F(t);
(2)将F(t)按步长间隔规则排列成列数分别为11列、12列、…、25列,行数为10行、11行、12行的对应矩阵,表1是T=11年的10行11列矩阵;
表1 太阳黑子磁场极性指数矩阵排列
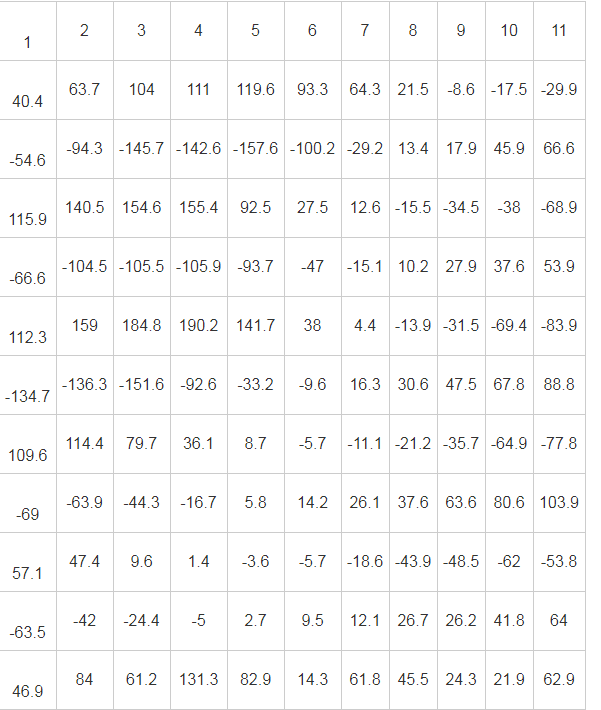
注:ΔF(t)=131.3-14.3=117.最后一行是各列数字的和.
(3)对于一系列行数相同列数不同的矩阵,分别将各矩阵中同列数值相加后取各矩阵列数据的最大值、最小值之差的绝对值|ΔF(t)|;
(4)以时间T为横坐标、|ΔF(t)|为纵坐标,绘制正排、逆排太阳黑子磁场极性数据索周曲线图.结果显示:太阳黑子磁场极性基础数据隐含的主、次周期(T1、T2)与索周曲线图中显示的主、次波峰所对应的横坐标周期值相等.研究表明:虽然选取矩阵的行数相同、列数不同,但仅在矩阵列数与选取数据隐含的实际周期相等或相近时,同列中最大值、最小值差的绝对值|ΔF(t)|才能取得最大,并且该周期性规律表现愈发明显.
为消除因数据排列方式的不同所导致的周期误差,进一步提高索周结果的准确性和精确度,对Whittaker和Robinson(1967)提出的索周法作进一步优化处理:(1)为消除首、尾数据对不同矩阵排列的影响,对相同的基础数据采用矩阵正排、逆排两种形式进行对比分析,提高索周结果的准确性;(2)为充分发挥较大数据量的优势,采用相同列数、不同行数或不同列数、相同行数排列形式进行对比研究;选择10行、11行、12行三种不同行数的矩阵进行索周处理,作横向比对参照,消除因矩阵行数的不同对索周结果准确性的影响.图2为10行、11行、12行三种不同行数矩阵的正排、逆排索周图(纵坐标经归一化处理).其中,图2a给出了三种行数矩阵的正排索周图,显示10行、11行、12行三种类型的矩阵排列分别表现出太阳黑子磁场极性指数具有22.50年、17.25年的周期性规律;图2b给出了三种行数矩阵的逆排索周图,显示10行、11行、12行三种类型的矩阵排列分别表现出太阳黑子磁场极性具有22.25年、18.50年的周期性规律.图2a与图2b比较可见,太阳磁场极性指数时间序列总体上呈现出平均22.375年的主周期和17.875年的次周期性规律;因此,以正排、逆排矩阵形式进行索周探求的周期结果与天文上的相关周期基本一致.通过正排、逆排进行索周处理,发现太阳黑子磁场极性指数显着存在22.25年的周期性规律,表2为10行、11行、12行三种不同行数矩阵的正、逆排索周对比结果.
表2 正、逆矩阵排列的周期结果
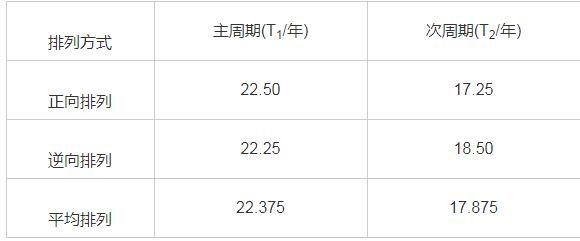
图2 太阳黑子磁场极性指数索周图
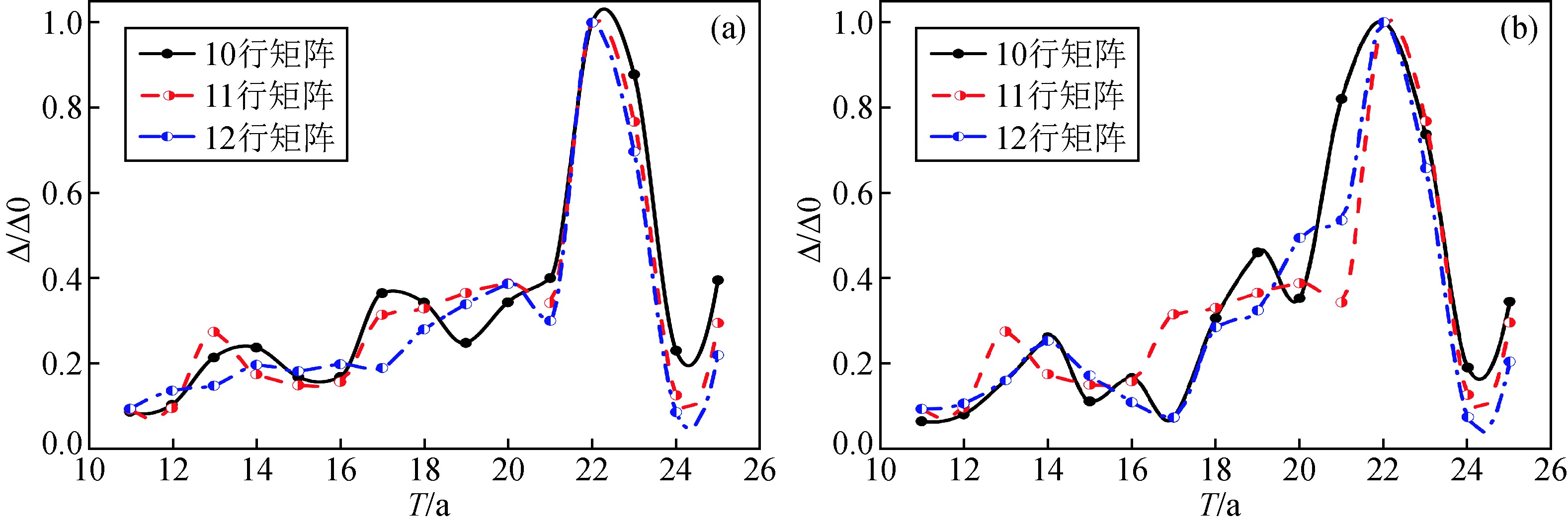
Fig.2 The cycle exploring map of the magnetic polarities of the sunspot magnetic field
2、 周期探求方法的对比分析
获得更加精确的太阳黑子磁场极性指数的周期性规律,有利于研究太阳活动与全球变化、地表环境演变和地球物理事件之间的关联性.综合上述按照步长为1年的索周探求步骤和过程,对比三种不同行数正排、逆排矩阵探求的结果表明:行数为10行的正排、逆排矩阵探索的周期结果更为准确.为进一步提高索周法所得周期结果的精度,拟采用以季度为基本时间间隔(即步长为0.25年),取行数为10行的矩阵进行索周处理,从1755年开始选取相对数F(t)并重复上述步骤进行索周处理,如图3所示.
图5 太阳黑子磁场磁极性数复Morlet小波分析实系数等值图
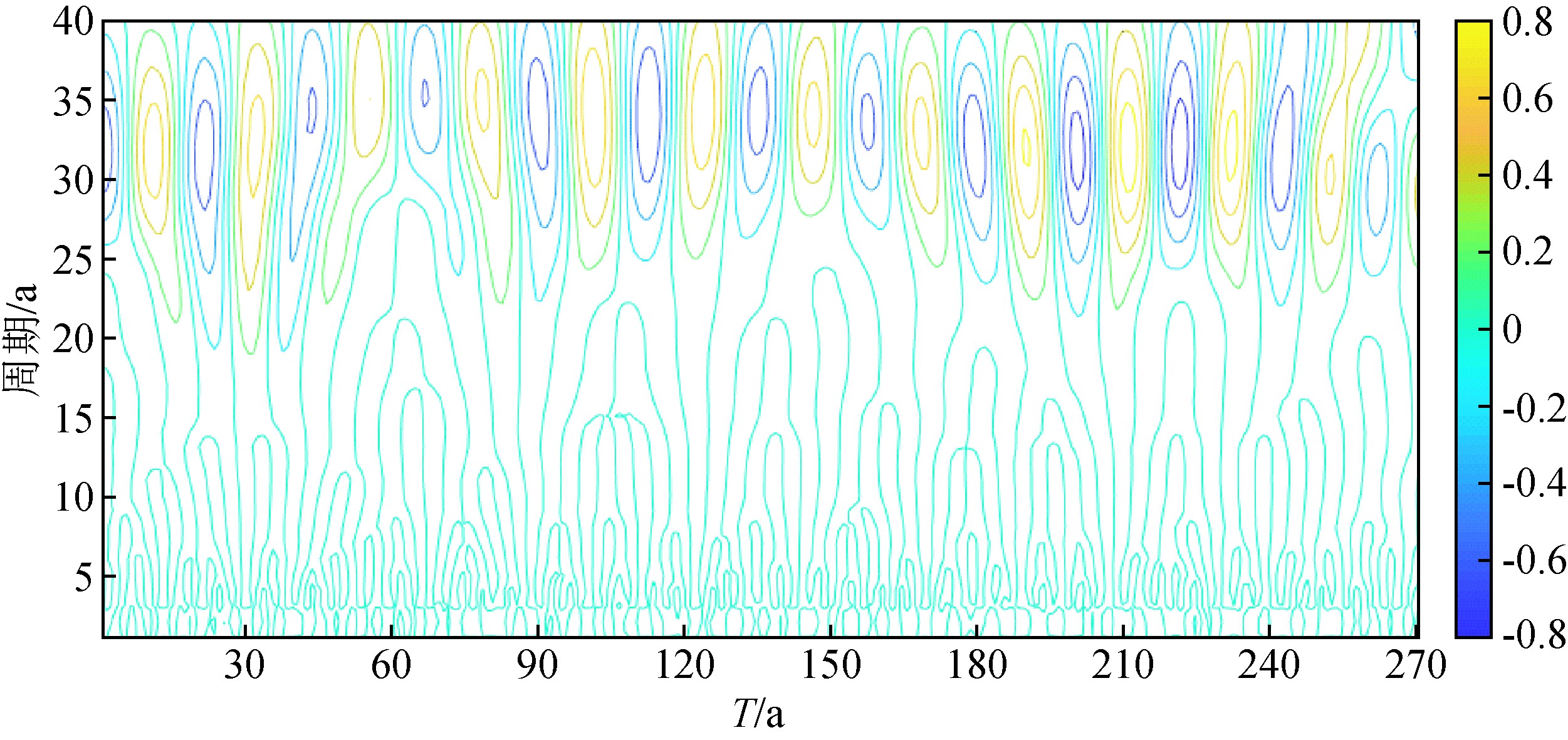
Fig.5 Equivalent graph of real Morlet wavelet analysis of the magnetic polarities of the sunspot magnetic field
图4 太阳黑子磁场磁极性数频率分布图
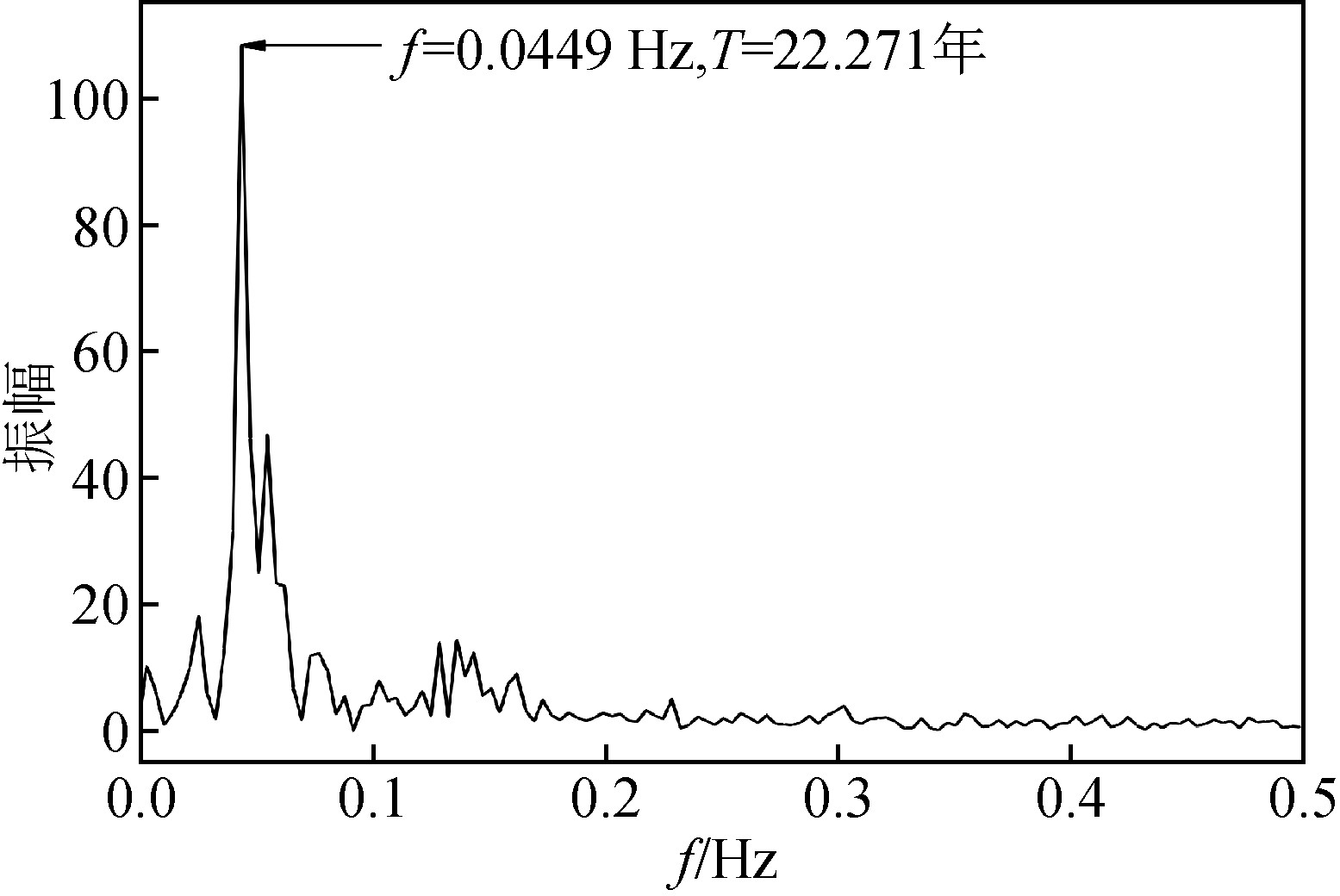
Fig.4 Frequency distribution diagram of magnetic polarity number of sunspot magnetic field
图6 1948—2000年太阳黑子磁性指数连续5个月滑动 平均曲线(除以150,细线)与北半球中纬度30°~ 50°10 hPa月平均温度264个月周期分量曲线 (粗线)(引自曲维政等2004图5)
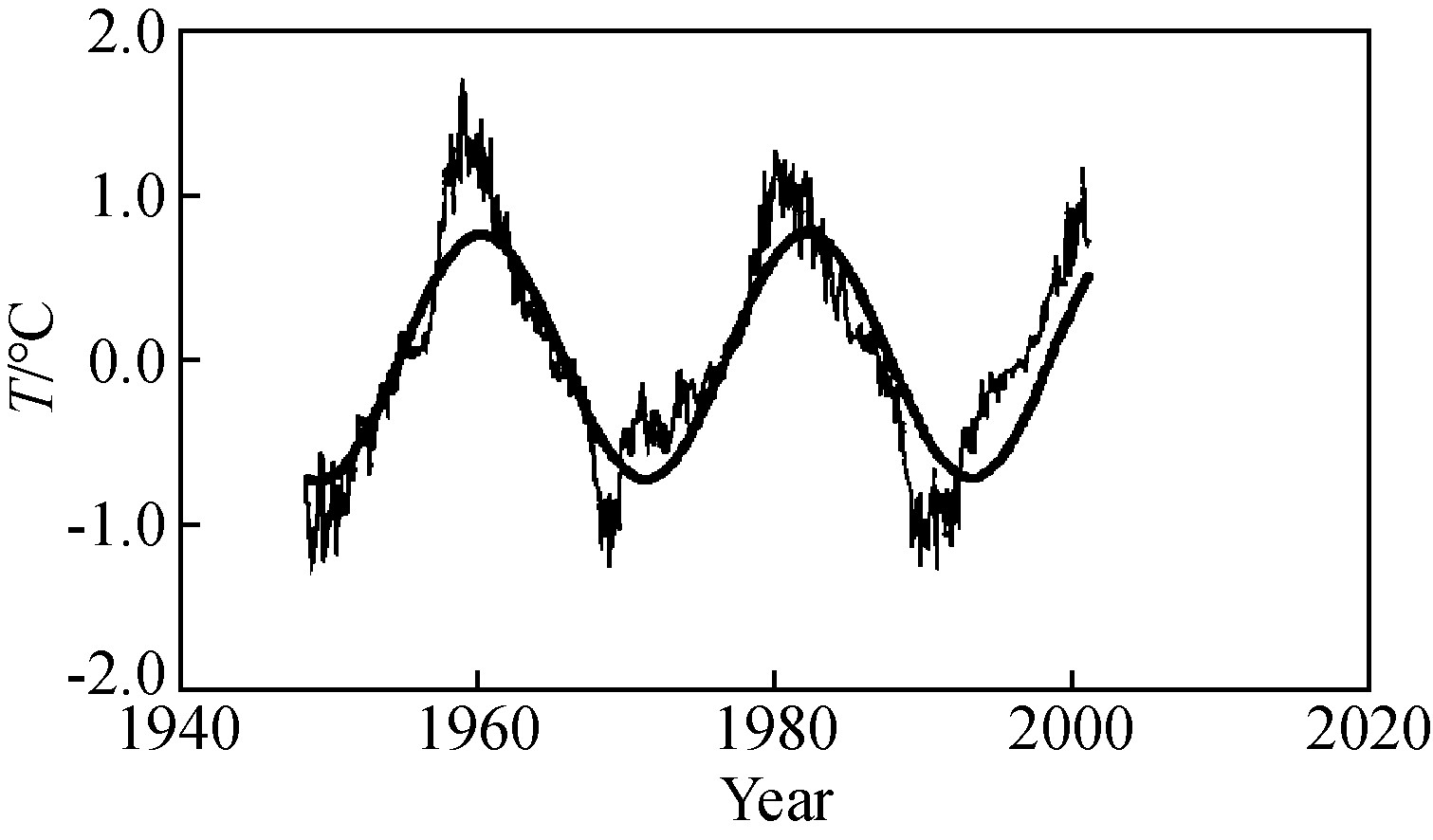
Fig.6 Magnetic exponent curve of sunspot(pided by 150, thin line)and 10 hPa monthly average temperature theoretic curve(thick line)of 264 months' cycle from 1948 to 2000 in 30°N~50°N(after figure 5 in reference Qu Wei-zheng, 2004)
按照年度、季度的时间尺度确定步长,进行多种行数矩阵正排、逆排分析,分别对太阳黑子磁场极性指数的基础数据进行索周处理.分析发现:处理的基础数据呈现明显22.25年左右的周期性规律,这一结果与曲维政等(2008)利用太阳黑子磁场磁性指数时间序列,探求得到的太阳活动磁极性平均22.20年周期相对一致.众所周知,太阳磁场在11年周期间隔中进行一次磁性倒转,这验证了在不考虑太阳黑子磁性变化前提下与准11年周期规律呈双倍关系.同时,国内外学者试图从太阳运动及太阳活动变化可能驱动全球气候周期性变化的机制出发进行相关研究.其中,曲维政等(2004)研究发现,太阳活动的22年磁性周期导致南北半球中纬度对流层和平流层大气温度场具有相同尺度的22年变化规律;进一步探究指明,太阳运动和太阳活动的周期性规律与全球气候和地表环境变化的周期性存在相似性(曲维政等,2007).同样,国内研究成果也表明我国长周期气候变化规律同太阳运动和太阳活动之间存在必然联系(竺可桢,1972;杨保等,2002);刘复刚等(2014)试图将太阳磁场变化与太阳轨道运动建立联系,尝试寻求满足两者变化曲线在相位上的对应关系,并与地球高层大气温度场谱联合分析显示:三者之间普遍存在准22年周期循环的关联,进而从更深层次角度阐释了影响全球气候变化的内因机制的联系.
伴随着计算机技术的日新更迭,傅里叶分析、功率谱估计、Morlet小波分析等应运而生,利用随机信号分析频率,逐渐成为获取时间序列周期性的得力工具.因此,这必将推动谱分析技术在水文气象、地球物理科学以及地质勘探等领域研究中得以广泛运用,其涉及研究对象包含各类信号、信息的判断和分析(王强和么枕生,1990).例如,功率谱在太阳黑子周期性分析、盛冰期太阳活动和中全新世东亚季风等天文学和地学研究领域中得以深入应用(吴江滢等,2006;李明霞等,2007;唐洁,2013).本文利用傅里叶分析方法和Morlet小波方式分析相同样本数据,试图揭示时间函数与频谱函数之间的内在联系,为索周法探求准确性高和精度值大的周期性规律提供佐证和对比,为后期准确构建太阳磁场极性指数时间序列提供重要理论指导和依据.
选取1749—2019年太阳黑子磁场极性数据,利用快速FFT分析得一系列数据组.图4给出了通过选定频率、振幅的列数据绘制频率变化曲线图.据谱分析曲线显示,频率f=0.0449即周期T=1/f=22.271年.因此,1749年至2019年近270年的太阳磁场极性指数时间序列存在显着22.271年的周期性变化规律;这一结果与基于索周法探寻太阳黑子磁极性得到22.25年周期性韵律高度吻合.傅里叶变换对于处理传统平稳信号分析发挥着特有的优势,能够快速建立时、频函数之间的内在关联;但是,在提取信号频谱过程中,必需提供完整的时域信息,缺乏对时域准确定位的能力,存在时间和频率分辨率上的双重局限性.随着实际研究需要的深入,为弥补傅里叶分析自身固有的缺陷,相应提出了多种较完备的分析途径,即使很大程度上改善了信号分析过程中暴露的既有缺陷,也依旧无法完全避免存在的短板问题.
Morlet小波常被应用于各种复杂信号的周期性规律解析,在信号学、天文气象、水利工程等研究领域有着颇为丰富的运用.借助Morlet小波分析1749—2019年太阳黑子磁极性数据,绘制出其复Morlet小波实系数等值图(图5).图5中横坐标表示选取数据涵盖的时间区间、纵坐标代表变化周期;正、负系数分别对应周期变化的波峰和波谷位置,系数的绝对值大小指代周期的显隐性强度;右侧彩色柱状图颜色从下至上,反映了幅值依次递增(黄色表示幅值较大,蓝色代表的幅值较小).观察Morlet小波分析的太阳黑子磁场磁极性数据的实系数等值图发现:太阳磁场极性指数时间序列存在较多尺度的周期分量,主要集中在21年至38年周期跨度.在此区间,出现不同幅度的振荡特征,一直贯穿于近270年的太阳磁场极性全部数据,具有全域性;总的来说,存在一组较连续的系列周期性变化规律.
Morlet小波改善了仅在全局框架下适用性较强的傅里叶分析,能很好地分析短时、局部不断变化的信号;由于小波基函数形式的多样性,恰恰给予了小波能被广泛应用的前提.正因小波基函数高度的灵活性,一定程度上无法避免,对于不同信号如何选择基函数种类、是否存在一个通用基处理信号分解任务、如何能无限制地细分时间和频率等一系列问题;尽管如此,分析中涉及消噪软硬阈值的准确选择、消除内容是噪声还是本身的所属信号等问题依然很难回答.因此,谱分析方法在信号周期探索中既有独特的优势,也有其不可忽略的弱点.
比较平均周期法、傅里叶分析和复Morlet小波分析三种周期分析法的流程和所得结果(表3).索周法较上述周期分析方式,能很好地控制误差范围,在提高求取周期结果的准确性和精度值方面具有良好优势.
就现状而言,针对上述不同的周期性分析途径,较索周法均具有不同程度的缺陷(表4);尤其在短周期规律的检测中,索周法凸显出独特的优势.同时,该方法能很好地贴合计算机程序算法,两者的协同参与成为减轻处理过程的繁琐性和提高结果准确性的关键.
鉴于索周法原理的提出,在一定程度上弥补了上述分析方式自身存在的局限性.它对数据的选取、排列、分析运算均基于数学角度的优化处理,规避了谱分析本身的分辨率低、谱线泄漏、基函数的正确选择和噪声消除软硬阈值的选取等一系列疑难问题.根据周期分析原理和被允许接受的误差范围,其结果精度由时间步长决定.因此,通过索周法所估算的周期性结果在误差范围内更易控制.考虑到实际计算的强度大小和结果的精度范围对于现有研究的影响,选取步长为1个季度所得结果的可控误差范围≤2.5%,完全适用于太阳磁场极性指数时间序列的周期性探究.基于周期规律分析的原理、处理步骤和结果,相对而言,较索周法均存在不同程度的缺陷.索周法既透射出处理过程的简洁性,又体现了探求周期结果的精准性;结合程序算法的协同参与,更大范围内减少处理过程的繁杂性和提高分析结果的准确性.
表3 不同周期分析方法处理流程和结果
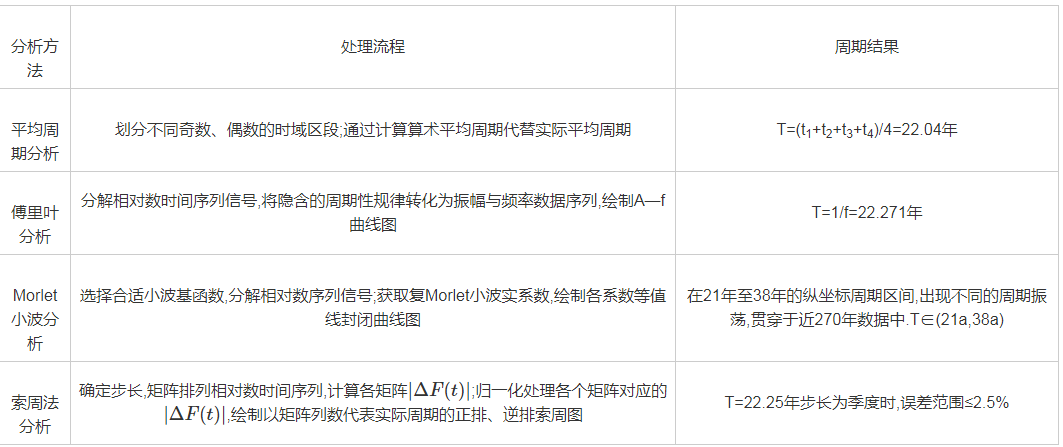
索周法分析确定步长,矩阵排列相对数时间序列,计算各矩阵|ΔF(t)|;归一化处理各个矩阵对应的|ΔF(t)|,绘制以矩阵列数代表实际周期的正排、逆排索周图T=22.25年步长为季度时,误差范围≤2.5%
表4 不同周期分析方法的优劣对比
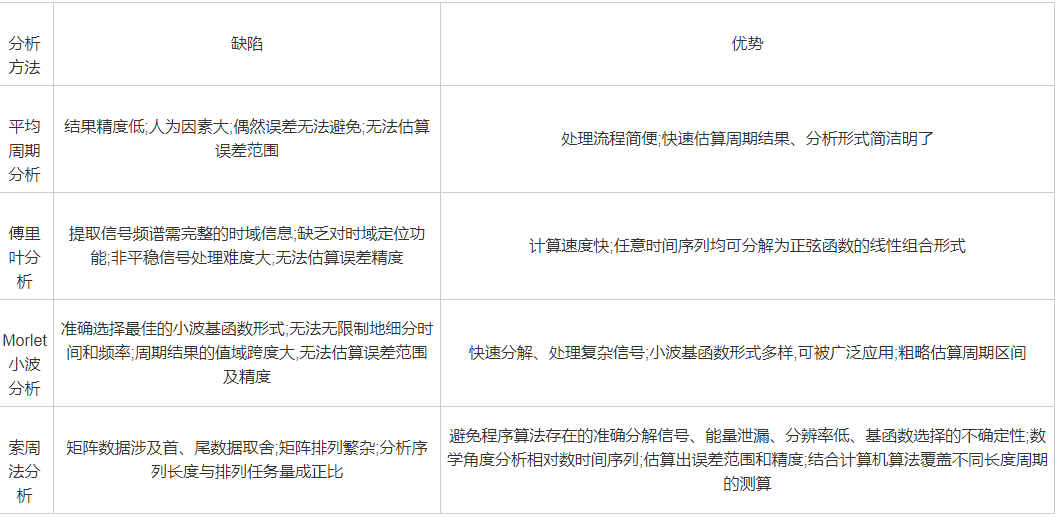
通过利用近300年来太阳黑子磁场极性指数数据进行索周处理,得到太阳黑子磁极性存在约22.25年周期性规律.这一结果,同太阳轨道运动诱发的北半球高空大气温度场变化准22年周期具有强烈一致性(刘复刚等,2014).曲维政等(2007)对在南北半球中纬度30°~50°、海平面1000 hPa到平流层中部10 hPa的 8个层次高度上大气温度频谱分析发现:各层次中的大气温度场存在与太阳磁场极性相同的22年周期性韵律.由此认为,大气温度场的22年变化周期是由太阳活动22年磁性所引发的(曲维政等,2004).由图6可知,曲维政等(2007)指出太阳活动磁性指数第10磁周~第12磁周,N极峰值年同温度准22年周期分量曲线相吻合;太阳活动磁性指数第9磁周~第11磁周,S极峰值年与温度准22年周期分量曲线相一致.曲维政等(2004)、刘复刚等(2014)一致认为,地球大气层受太阳磁场磁性周期性变化的影响是全球性的,从这一关系中清晰阐明了太阳的周期性活动与全球气候、地表环境变化存在固有联系.
因此,太阳活动引发的太阳磁场耦合,导致太阳黑子磁极性数值的变化,进而指明了大气温度场变化规律.这一思想给予了我们颇为强烈的启示,建立直接或间接分析指标,进行内因机制的关联性研究,或将为太阳运动与全球气候及地表环境演变问题的探讨,提供极具重要的参考和借鉴.
索周法不仅能精确探求隐含于时序数据中的多种短周期韵律,也可有效覆盖其在中、长周期规律的探索.随着索周法处理步骤的日臻完善,既佐证谱分析的周期结果,又提高周期估算结果的精度.期望多种周期分析方式之间能够相辅相成地发展,最终为研究太阳周期性活动所诱导的外部空间环境监测、全球气候及地表环境演变等前沿问题,给予理论指导和科学预测.
3、结论与讨论
(1)通过索周法探求太阳黑子磁场极性指数,结果显示具有准22.25年的周期性韵律.此结果与分析太阳磁场极性指数时间序列MI得到的22.2年周期基本一致,从新的角度对太阳运动及太阳活动具有的周期性规律进行佐证.
(2)通过索周法对太阳运动及太阳活动的基本标志——太阳黑子磁场极性指数周期的探求,其结果与已取得的研究成果保持相对一致性.在周期的数值上,不仅与太阳轨道运动平均22年的恒星周期、太阳自转速度变化的准22年周期高度契合,而且同地球高层大气温度场准22年周期结果具有密切的关联性.从而为进一步分析诱发全球气候变化、地表环境演变的天文因子奠定理论基础.
(3)索周法能够有效检索出不同尺度的周期性规律,兼具估算误差范围和提高结果精度的双重优势.同时,索周法的完善避免了主流谱分析(功率谱估计和小波分析)所无法回避的缺陷,如分辨率低、谱线泄漏、基函数和噪声消除的软硬阈值的正确选择等.期望程序算法的协同参与,满足多种尺度周期成分的检测,最终为研究太阳周期性活动所诱导的外部空间环境监测、全球气候及地表环境演变等前沿科学,提供科学指导和精准预测.
参考文献
Babcock H W.1961.The topology of the Sun's magnetic field and the 22-year cycle [J].The Astrophysical Journal,133:572-587.
[]Charvátová I.2000.Can origin of the 2400-year cycle of solar activity be caused by solar inertial motion [J].Annales Geophysicae,18(4):399- 405.
[]Chen B,Yin C L.1965.On periodicities of solar activity [J].Acta astronomica sinica (in Chinese),13(01):89-96.
Hale G E,Seth Barnes Nicholson.1938.Magnetic observations of sun-spots 1911-1924 [J].Washington D.C.Carnegie of Washington,(1):1.
Hood L L,Jirikowic J L.1991.A probable 2400 year solar quasicycle in atmospheric D 14C [J].Holocene,12:98-105.
Jose P D.1965.Sun's Motion and Sunspots [J].The Astronomical Journal,70(3):193-200.
Krivova N A,Vieira L E A,Solanki S K.2010.Reconstruction of solar spectral irradiance since the Maunder minimum [J].Journal of Geophysical Research,115(A12):A12112.
[]Li K J,Feng W,Liang H F.2010.The abnormal 24th solar cycle—The first complete solar cycle of the new millennium [J].Scientia Sinica (Physica,Mechanica & Astronomica) (in Chinese),40(10):1293-1301.
[]Li M X,Wang Y J,Qiu Q L.2007.High Resolution Stalagmite Records of East Asian Monsoon from 7 to 6 ka B.P.in Mid-Holocene [J].Scientia Geographica Sinica (in Chinese),27(4):519-524.
[]Liu F G,Qu W Z,Wang J,et al.2014.Orbital motion and magnetic variation of Sun:Relation to 22-year cycle of the upper atmospheric temperature of Earth [J].Progress in Geophysics (in Chinese),29(2):512-517,doi:10.6038/pg20140206.
[]Liu F G,Wang J,Shang Z Y,et al.2013b.Study on long-term cyclical rhythm of solar activity [J].Progress in Geophysics (in Chinese),28(2):570-578,doi:10.6038/pg20130205.
Qu W Z,Deng S G,Huang F,et al.2004.Influence of magnetic index abnormal change in the solar magnetic field on climate at the middle latitudes of naorth hemisphere [J].Chinese Journal of Geophysics (in Chinese),47(3):398- 404,doi:10.3321/j.issn:0001-5733.2004.03.005.
[]Qu W Z,Huang F,Zhao J P,et al.2007.The significance of solar magnetic field direction variation on anomalous variability of the atmosphere temperature on the earth [J].Chinese Journal of Geophysics (in Chinese),50(5):1304-1310,doi:10.3321/j.issn:0001-5733.2007.05.005.
[]Qu W Z,Qin T,Deng S G,et al.2008.The time sequence of the magnetic index of the sunspot magnetic field [J].Progress in Geophysics (in Chinese),23(06):1727-1735.
Schwabe H S.1843.Solar observation during 1843 [J].Asttron Nachr,20(495):234-235.
Sonett C P,Finney S A.1990.The spectrum of radiocarbon [J].Royal Society of London Philosophical Transactions,330(1615):413- 425.
[]Suess H E.1980.The radiocarbon record in tree rings of the last 8000 years [J].Radiocarbon,22(2):200-209.
Sun W,Wang J,Chen J R,et al.2017.Modeling of the planet juncture index and heliocentric longitude of the centroid of planetary systems and numerical simulation [J].Progress in Geophysics (in Chinese),32(02):506-515,doi:10.6038/pg20170208.
[]Sun W,Wang J,Chen J R.,et al.2017.Variations of the planet juncture index and heliocentric longitude with spectral analysis for approximately 2000 years [J].Chinese Science Bulletin (in Chinese),62(05):407- 419,doi:10.1360/N972016- 00447.
[]Tlatov A G.2007.22-year variations of the solar rotation and solar activity cycles [J].Astronomy Letters,33(11):771-779.
[]Tang J.2013.Periodicity analysis based on power spectrum estimation [J].Journal of Shaanxi University of Technology (Natural Science Edition) (in Chinese),29(5):71-74,doi:10.3969/j.issn.1673-2944.2013.05.016.
[]Tang J,Liu X Q.2018.Analysis of multiple time scales feature and chaotic property for time series of relative sunspot numbers [J].Scientia Sinica (Physica,Mechanica & Astronomica) (in Chinese),48(2):103-110,doi:10.1360/SSPMA2017- 00260.
[]Wang Q,Me Z S.1990.Discussions on some key problems in power spectra analysis [J].Acta Geographica Sinica (in Chinese),45(3):363-372,doi:10.3321/j.issn:0375-5444.1990.03.012.
Whittaker E T,Robinson G..1967.The calculus of observations:An introduction to numerical analysis [M].Dover Publications Inc New York.
Whittaker S E,Robinson G.1944.The calculus of observations [M].London:Blachic & Son Limited.
[]Wu J Y,Shao X H,Kong X G,et al.2006.The imprinting of solar activity during the glacial period in the sequence of stalagmites in Nanjing [J].Chinese Science Bulletin (in Chinese),51(4):431- 435,doi:10.3321/j.issn:0023- 074X.2006.04.012.
[]Wu S W,Guo S L,Lin F,et al.2014.Influence of Magnetic Index Change in Solar Magnetic Field on Intensity of East Asian Summer Monsoon [J].Science Technology and Engineering (in Chinese),14(05):187-191,doi:10.3969/j.issn.1671-1815.2014.05.037.
[]Yang B,Shi Y F,Zhou Q B.2002.Analyzing the Effect of Solar and Volcanic Activities on Temperature Variations in the Guliya Ice core Record and in the Lower Reaches of the Yangtze River over the Last Three Centuries [J].Journal of Glaciology and Geocryology (in Chinese),24(1):40- 45.
Yang C X,Wu H F,Hu D T.2011.Relationship between air temperature oscillations and solar variability on short and medium time scales [J].Sci China Earth Sci (in Chinese),41(03):413- 424,doi:10.1007/s11430- 010- 4161-2.
Yang D H,Yang X X.2013.Study and model on variation of Earth's Rotation speed [J].Progress in Geophysics (in Chinese),28(01):58-70,doi:10.6038/pg20130107.
Zhan L S,He J M,Ye Y L,et al.2006.Periodicity Analysis of Solar Activity by Wavelet Analyzing Method [J].Acta astronomica sinica (in Chinese),47(2):166-174,doi:10.3321/j.issn:0001-5245.2006.02.005.
[]Zhao P Z,Chen J,Zhao W T.2001.The sunspots affect elnino and lanina [J].Progress in Geophysics (in Chinese),16(3):85-90,doi:10.3969/j.issn.1004-2903.2001.03.011.
[]Zhao X H,Feng X S.2014.Periodicities of solar activity and the surface temperature variation of the Earth and their correlations [J].Chinese Science Bulletin (in Chinese),59(14):1284-1292,doi:10.1360/972013-1089.
Zhu K Z.1972.A preliminary study of climate change in China in the past five thousand years [J].The Chinese Journal of Archaeology (in Chinese),01(01):15-38.
Zuo X M,Wan W X.2002.The correlation between sporadic e-layer and solar activity [J].Chinese Journal of Geophysics (in Chinese),45(6):759-765,doi:10.3321/j.issn:0001-5733.2002.06.002.
陈彪,印春霖.1965.关于太阳活动周期——相对数曲线的一种数学表达式[J].天文学报,13(01):89-96.
李可军,冯雯,梁红飞.2010.异常的第24太阳活动周——新千年的第一个完整的太阳活动周[J].中国科学:物理学力学天文学,40(10):1293-1301.
李明霞,汪永进,邱庆伦.2007.中全新世7~6 ka东亚季风气候的高分辨率石笋记录[J].地理科学,27(04):519-524.
刘复刚,曲维政,王建,等.2014.太阳轨道运动—太阳磁场变化与地球高层大气温度准22年周期循环的联系[J].地球物理学进展,29(2):512-517,doi:10.6038/pg20140206.
刘复刚,王建,商志远,等.2013b.太阳轨道运动长周期性韵律的成因[J].地球物理学进展,28(2):570-578,doi:10.6038/pg20130205.
[]曲维政,邓声贵,黄菲,等.2004.太阳磁场磁性指数异常变化对南北半球中纬度气候的影响 [J].地球物理学报,47(3):398- 404,doi:10.3321/j.issn:0001-5733.2004.03.005.
曲维政,黄菲,赵进平,等.2007.太阳磁场方向变化对于地球大气温度异常变化的意义[J].地球物理学报,50(5):1304-1310,doi:10.3321/j.issn:0001-5733.2007.05.005.
曲维政,秦婷,邓声贵,等.2008.太阳黑子磁场极性指数时间序列 [J].地球物理学进展,023(006):1727-1735.
[]孙威,王建,陈金如,等.2017.行星会合指数与行星系质心的日心经度模型构建及数值模拟 [J].地球物理学进展,32(02):506-515,doi:10.6038/pg20170208.
孙威,王建,陈金如,等.2017.近两千年以来行星会合指数与行星系日心经度变化及频谱分析[J].科学通报,62(05):407- 419,doi:10.1360/N972016- 00447.
唐洁.2013.功率谱分析方法在周期分析中的应用[J].陕西理工学院学报:自然科学版,29(5):71-74,doi:10.3969/j.issn.1673-2944.2013.05.016.
唐洁,刘晓琴.2018.太阳黑子相对数的多时间尺度及混沌特性分析[J].中国科学:物理学力学天文学,48(2):103-110,doi:10.1360/SSPMA2017- 00260.
王强,么枕生.1990.功率谱分析中几个重要问题的讨论[J].地理学报,45(3):363-372,doi:10.3321/j.issn:0375-5444.1990.03.012.
[]吴江滢,邵晓华,孔兴功,等.2006.盛冰期太阳活动在南京石笋年层序列中的印迹[J].科学通报,51(4):431- 435,doi:10.3321/j.issn:0023- 074X.2006.04.012.
吴姗薇,郭胜利,林帆,等.2014.太阳磁场磁性指数对东亚夏季风的影响[J].科学技术与工程,14(05):187-191,doi:10.3969/j.issn.1671-1815.2014.05.037.
杨保,施雅风,周清波.2002.近300a来古里雅与长江下游温度变化所受太阳活动、火山活动的影响分析[J].冰川冻土,24(1):40- 45.
[]杨春霞,伍宏发,胡丹婷.2011.短中时间尺度上的气温变化和太阳辐射之间的关系研究[J].中国科学:地球科学,41(03):413- 424,doi:10.1007/s11430- 010- 4161-2.
[]杨冬红,杨学祥.2013.地球自转速度变化规律的研究和计算模型[J].地球物理学进展,28(01):58-70,doi:10.6038/pg20130107.
[]占腊生,何娟美,叶艺林,等.2006.太阳活动周期的小波分析[J].天文学报,47(2):166-174,doi:10.3321/j.issn:0001-5245.2006.02.005.
赵佩章,陈健,赵文桐.2001.太阳黑子对厄尔尼诺、拉尼娜的影响 [J].地球物理学进展,16(3):85-90,doi:10.3969/j.issn.1004-2903.2001.03.011.
赵新华,冯学尚.2014.太阳活动与地球表面温度变化的周期性和相关性 [J].科学通报,59(14):1284-1292,doi:10.1360/972013-1089.
[]竺可桢.1972.中国近五千年来气候变迁的初步研究 [J].考古学报,01(01):15-38.
[]左小敏,万卫星.2002.电离层突发E层与太阳活动的相关性[J].地球物理学报,45(6):759-765,doi:10.3321/j.issn:0001-5733.2002.06.002.