运用高级个人旅行费用法估算汉口江滩的游憩价值

　　旅游资源的调查、 分类与评价已经成为旅游开发中的基本内容，由于旅游资源的公共属性，其价值难以确定。 旅行费用法（TCM）是对环境资源 （包括旅游娱乐资源和各类游憩活动 ）经济价值进行评估的主要方法。旅行费用法是由美国的克劳森（Clawson）于 1959 年提出。 由于 TCM 评估具有较强的科学性， 所以在美国、 加拿大和欧洲，TCM 方法的应用相当广泛 。 布朗 （Brown） 和纳瓦斯 （Nawas） 在1973 年提出应在个体旅游者调查样本的基础上估计旅游景区的经济价值，提高估计的有效性。

　　对于旅游资源的游憩价值， 目前，国内多选用分区旅行费用法来评价。 李巍、李文军 等学者（2003）用旅行费用区间分析（TCIA）。 张茵（2004）针对多目的地问题，提出了基于分区的多目的地 TCM 模型（MZTC），并应用于九寨沟的游憩价值评估中。 郝伟罡（2007）在 TCIA 基础上提出对游客样本进行分组的新型旅行费用区间分析的计算方法。 谢双玉 等学者（2008）从积分的角度对 TCIA 与传统的分区旅行费用法（ZTCM）的数学本质进行了详细的对比分析。 杨净、许丽忠 等学者（2012）对鼓山风景名胜区进行评估，通过 ITCM 计算消费者剩余。 赵玲、王尔大、苗翠翠等学者针对中国旅游者出行方式的特点， 设计改进的 ITCM 模型。

　　多数学者使用分区旅行费用法（ZTCM）计算游憩价值。 利用个人旅行费用法计算游憩价值的案例较少。

　　本文高级个人旅行费用法对武汉市汉口江滩的游憩价值进行估算，并在此基础上，对如何科学制定汉口江滩的投资策略，如何改善景区管理效率等提出建议。

　　1、 TCM模型简介

　　1．1 分区旅行费用法（ZTCM）

　　ZTCM 模型的必要条件是参与分析的数据必须是区域一级的，对游客根据其客源地进行分区是必不可少的。 ZTCM 通常具有如下模型形式：Vij／ Ni＝F（TCij，SOCi，SUBi） 公式（1）式中，Vij表示一定时间内从 i 区域到 j 旅游地旅游的总人数；Ni表示 i 区域的人口总数；TCij表示 i 区域游客到 j 旅游地的平均旅行费用；SOCi表示 i 区域旅游者的社会经济特点；SUBi表示 i 区域旅游者旅游替代品的特点。 ZTCM 是单目的地模型，对于相对平均分布的旅游者出发地的情况较为适用。 ZTCM 适用于重游率较低的吸引长线游客的观光型目的地。

　　1．2 个人旅行费用法（ITCM）

　　ITCM 的需求函数一般具有如下形式：Vij＝F（TCij，SOCi，SUBi） 公式（2）式中，Vij表示一定时间内个体 i 到 j 旅游地旅游次数；TCij表示个体 i 区域游客到 j 旅游地的旅游一次的费用；SOCi表示 i 区域旅游者的社会经济特点；SUBi表示 i 区域旅游者旅游替代品的特点。 ITCM 是单目的地模型，依靠观测数据的内在变化而不是对区域数据的聚合来进行回归。 但是由于它通常仅包括实际到访过的游客，而排除了非游客的信息。 这被称为“截断偏差”。 如果评估对象是吸引范围较大、重游率较低的观光型目的地，可能会因“因变量离散不足”而无法拟合需求函数，因此，ITCM 适用于吸引当地短途旅客、重游率较高的休闲游憩型目的地。

　　1．3 高级个人旅行费用法（AITCM）

　　为了避免个人旅行费用法（ITCM）的缺陷，截断模型等较为高级的计量经济模型被应用于计算游憩价值， 应运而生的就是高级个人旅行费用法（AITCM）。较为常用的两种模型是截断泊松模型（TPois）和截断负二项模型（TNB）。 但是，AITCM 仍然没有解决 ITCM“因变量离散不足”的问题。

　　2、案例研究地

　　2．1 基本概况

　　汉口江滩所处的武汉市位于北纬 30．6 度，东经 114．1 度，海拔 23 米，属亚热带季风气候区。 汉口江滩是“亚洲第一大江滩”，位于中国内陆最大城市武汉市区北岸，是一个集旅游、休闲、健身、绿化、娱乐为一体的大型文化公园，面积 160 万平方米，与沿江大道景观相邻，与“天下江山第一楼”———黄鹤楼景区相望，与长江百舸争流盛况相映，构成武汉市中心区独具魅力的景观。 近两年来，由于服务设施的完善与交通的便捷等，汉口江滩的旅游人次不断增长。

　　本研究于 2013 年 10 月 1 日到 10 月 8 日黄金周期间，采用随机抽样的方法，对汉口江滩的游客进行半访谈式的问卷调查。

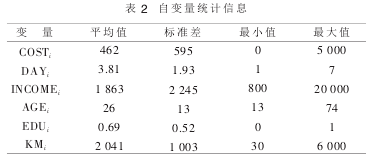
　　共发放问卷 962 份，回收有效问卷 857 份，有效率为 89％。 调查对象主要为外地观光游客和休闲锻炼的当地市民， 调查内容包括两类问题：一类是与游览有关的情况及其费用（包括此行的起点、交通方式及费用、旅行距离、游览的其他景点个数、旅行时间、公园内支出等）；另一类是游客的人口统计资料（包括性别、年龄、文化程度、月收入、职业等）。 样本到汉口江滩旅游次数统计信息见表 1。

　　计算可得，汉口江滩平均旅游次数为 2．73 次，方差为 3．40。

　　TCM 模型中的因变量， 即旅游次数离散不足的情况并不是十分明显。

　　2．2 TCM 模型的选择

　　ZTCM 是单目的地模型，适用于估算旅游者出发地相对平均分布的情况。 假设游客来自同一区域，对某个旅游点具有相同偏好，且旅行费用相同。这种情况显然不符合现实情况。而 ITCM 的缺陷，即对于评估对象是吸引范围较大、重游率较低的观光型目的地，可能会因为“因变量离散不足”而无法拟合需求函数。 汉口江滩的重游率较高，且“因变量离散不足”的情况并不明显。 为了克服由于缺少非游客信息造成的“截断偏差”，采用 AITCM 模型。

　　AITCM 模型中两个理论上最为完备的截断离散模型是 TPois 和TNB，而 TPois 模型中要求因变量的方差－期望等于 1，这种限制较为苛刻，汉口江滩方差－期望为 1．245，不符合该条件；TNB 模型对方差－期望比的限制值域为［1，＋∞）。 本研究所获样本中，因变量方差－期望比仅为 1．245，显然符合 TNB 模型的值域要求。

　　2．3 AITCM 高级个人旅行费用法模型

　　对某一景点的旅游需求可以用旅游者在一定时间段访问该景点的次数来表示。 一般来说，旅游需求可以表示为：Qi＝F（X，准，ε） 公式（3）i＝1，2，3，…，n式中，Qi是 1×n 维的因变量向量，表示旅游者到目的地的次数；X 是自变量矩阵，表示旅游需求的影响因素，如旅游费用、教育程度、年龄、旅游距离等；准 是参数向量，表示自变量系数估计值；ε 是独立、均等分布的随机误差向量。

　　旅游需求函数一般是通过收集旅游者的信息， 因此建立的模型有旅游次数数据为非负整数的缺陷。 在需求模型中，作为因变量的旅游次数服从非负整数的某类概率分布， 其取值是一个计数过程， 所以计数数据的截断性质要求采用一些特殊模型参数估计方法。 由于参加旅游次数数据是整数，并在零点截断，且表现出过度离散的问题，因此，最小二乘（OLS）方法不再适用于这类函数的参数估计。 为了获得无偏差的参数估计结果，采用截断负二项分布计数数据模型，其概率密度函数如下：

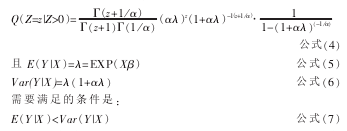
　　式中，随机变量 Z 的均值是 λ，方差是（λ+αλ2）；α＞0 是多余参数，Γ（）是伽玛函数，z 是非负整数集的一个元素，式（5）式（6）分别是 NB 分布的已接矩阵和未接矩阵，变量的定义与式（3）相同。

　　考虑到旅游次数数据具有的非负整数和截断性质， 本研究采用 TNB 截断负二项分布计数数据模型， 可用似然法进行参数估计。 因变量的概率分布如下：

　　Y＝NB（λ＝EXP（Xβ），α），Y>0 公式（8）式中，X 为解释变量矩阵；β 是参数变量。

　　2．4 计算结果

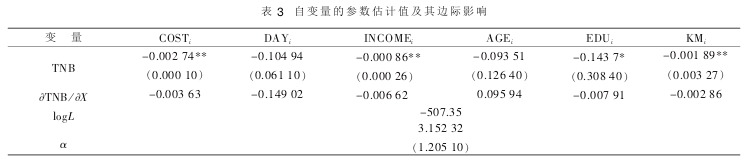
　　回归模型的因变量 Qi为第 i 个旅游者到旅游地的旅游次数；自变量 COSTi为第 i 个旅游者到旅游地旅行产生的复合旅行成本；自变量 DAYi为第 i 个旅游者在该旅游地的停留时间；自变量 INCOMEi为第 i 个旅游者的月收入； 自变量 AGEi为第 i 个旅游者的年龄；自变量 EDUi为第 i 个旅游者的受教育程度；自变量KMi为第 i 个旅游者的旅行距离（计算结果见表 2、表 3）。

　　这可能是由于汉口江滩提供的旅游产品质量较低， 随着人们收入的提高， 人们更愿意到质量更高的旅游景点。 这与旅行距离KMi与旅游次数 Qi应为负相关关系，即旅行成本越高，旅行距离越远，旅游次数应该越少。 DAYi停留时间、月收入 INCOMEi与旅游次数 Qi应该呈正相关关系，即停留时间越长，月收入越多，旅游次数应该越多。 年龄 AGEi、受教育程度 EDUi以及其他变量根据旅游景点类型和性质的不同， 也会与旅游次数有不同的相关关系。

　　旅游景点的价值可以通过旅游需求函数来确定。 通过计算模型中旅行成本变量参数估计的负倒数， 可以测算旅游消费者剩余，即 364．96 元。

　　根据武汉市旅游局的数据，2012 年度汉口江滩的年度旅游人次为 1 500 万人次， 由此可以计算出汉口江滩的游憩价值为54．74 亿元。

　　3、结 论

　　由于一个黄金周的抽样调查数据， 不能全面反映汉口江滩全年旅游者的实际情况和特点，游憩价值的估算不一定准确。 多目的地、 替代景点问题以及旅游者偏好等问题在本文中没有考虑其中，为了加强对旅游者行为的分析，今后也可以更多地引入完善的 GIS 数据采集与分析系统，完善游憩价值的评估。

　　参考文献：
　　［1］J Benson，K G F Willis. Valuing Informal Recreation on the ForestryCommission estate［J］．Quarterly Journal of Forestry， 1993 （3）：63 －65．
　　［2］M Clawson，L J Knetsch．The Economics of Outdoor Recreation ［M］．Baltimore Md：John Hopkins Press，1996．
　　［3］薛达元，包浩生，李文华．长白山自然保护区生物多样性旅游价值研究［J］．自然资源学报，1999（2）：140－145．
　　［4］李巍，李文军．用改进的旅行费用法评估九寨沟的游憩价值 ［J］．北京大学学报，2003（39）：548－554．
　　［5］张茵，蔡运龙．基于分区的多目的地模型及其在游憩资源价值评估中的应用———以九寨沟自然保护区为例［J］．自然资源学报，2004（19）：651－660．
　　［6］郝伟罡．环境价值评估 ———旅行费用法 ［J］．中国人口·资源与环境 ，2009（1）：70－75．
　　［7］谢双玉，訾瑞昭，许英杰．旅行费用区间分析法与分区旅行费用法的比较及应用［J］．旅游学刊，2008（2）：41－45．
　　［8］杨净，许丽忠．基于 ITCM 的游憩价值评估 ———以鼓山风景名胜区为例［J］．福建师范大学学报，2012（28）：89－94．
　　［9］赵玲，王尔大，苗翠翠．ITCM 在我国游憩价值评估中的应用及改进［J］．旅游学刊，2009（24）：63－69．
　　［10］赵强 ，李秀梅 ，谷长强．旅行费用法 （TCM）研究 ［J］．济南大学学报 ，2008（2）：213 －219．
　　［11］艾运盛，张鸿雁．旅行费用法在游憩效益评价应用中的问题及对策研究［J］．林业经济问题，1996（2）：24 －27．
　　［12］陈浮，张捷．旅游价值货币化核算研究———九寨沟案例分析［J］．南京大学学报，2001（3）：296－304．