探讨傅利叶变换频谱分析方法用于高分子材料实验

  0 引 言.

    高分子材料是一定组成配合的高分子化合物( 由主要成分树脂或橡胶和次要成分添加剂组成 在成型设备中,受一定温度和压力的作用熔融塑化,然后通过模塑制成一定形状,冷却后在常温下能保持既定形状的材料制品。任何一种高分子材料都呈现一种粘弹性的特点,即在常温下既有一定的粘性又具有一定的弹性“可以说高分子材料就是不同数量的虎克弹簧和牛顿粘壶以不同的方式组合而成的,其在力学的表现上也就有所不同。在受到外力的冲击时所表现出来的特性也不尽相同“在受到冲击时,冲击作用将会在材料内部形成传递”当冲击速度很快,所用时间很短时,粘弹性材料在这种传递的过程中,将会输出比较宽的频谱“频谱是对材料力学性能的一个重要的表征,特别对试验时会产生显著的几何变形的塑性材料。因此,为了更好的研究不同材料的力学性能,就要从中得到一些关于不同材料或同一材料在不同温度下的力学性质,也就是要对材料频谱进行分析“目前关于频谱分析中运用最多,用途最广,效果最好的分析方法是通过傅利叶变换来分析”. 材料的粘弹性及傅里叶变换所谓材料的粘弹性也就是介于理想弹性固体和理想粘性液体之间,既具有固体的弹性又具有液体的粘性。

   1 、材料的粘弹性及傅里叶变换

    所谓材料的粘弹性也就是介于理想弹性固体和理想粘性液体之间,既具有固体的弹性又具有液体的粘性[6].理想弹性固体具有一定的形状,在外力作用下,发生形变到一新的平衡的形状,在除去外力时,它又完全恢复到起始的形状. 也就是说固体把外力在形变时所做的功完全储存起来了,当去除外力时,这个能量使它完全回复到原始的形状,而且这种形变和回复过程都是瞬时完成的.理想的弹性固体的力学行为可以用虎克定律来描述[7].理想粘性液体没有一定的形状,在外力作用下发生不可逆的流动,形变随时间的增加而增加,外力所做的功以热的形式散失掉.理想的粘性液体的力学行为可以用牛顿定律来描述[8],常称为牛顿流体,随着科学的迅猛发展,高分子材料已经广泛运用于各个行业,而高分子材料的粘弹性与时间有关,被称为高分子材料的力学松弛.设想用理想弹簧当成力学单元以不同方式的组合来模拟聚合物的力学松弛过程[9].

    目前关于频谱分析中运用最多,用途最广,效果最好的分析方法是通过傅利叶变换来分析.将时域变为频域的变换,称之为傅立叶正变换; 而将频域变为时域的变换,称之为傅立叶逆变换[10].傅立叶分析提供了获取频域信息的一种较为完整的方法,它使我们利用频率,幅值和相位来描述时域中的振动波形.

    快速傅氏变换,是离散傅氏变换的快速算法,它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的.其实质就是设 x( n)为 N 项的复数序列,由 DFT 变换,任意 X( m) 的计算都需要 N 次复数乘法和 N -1 次复数加法,而 1 次复数乘法等于 4 次实数乘法和 2 次实数加法,1 次复数加法等于 2 次实数加法,即使把 1 次复数乘法和 1 次复数加法定义成 1 次“运算”( 4 次实数乘法和 4 次实数加法) ,那么求出 N 项复数序列的 X( m) ,即 N 点DFT 变换大约就需要 N2次运算.当 N =1 024 点甚至更多的时候,需要 N2= 1 048 576 次运算,在 FFT 中,利用 WN 的周期性和对称性,把一个 N 项序列( 设 N =2k,k 为正整数) ,分为 2 个 N /2 项的子序列,每个 N /2点 DFT 变换需要( N/2)2次运算,再用 N 次运算把两个 N/2 点的 DFT 变换组合成一个 N 点的 DFT 变换.

    这样变换以后,总的运算次数就变成 N + 2( N/2)2=N + N2/2.继续上面的例子,N = 1 024 时,总的运算次数就变成了 525 312 次,节省了大约 50% 的运算量.

    而如果我们将这种“一分为二”的思想不断进行下去,直到分成两两一组的 DFT 运算单元,那么 N 点的 DFT变换就只需要 N·log2N 次的运算,N 在 1 024 点时,运算量仅有 10 240 次,是先前的直接算法的 1%,点数越多,运算量的节约就越大,这就是 FFT 的优越性.

    它对傅氏变换的理论并没有新的发现,但是对于在计算机系统或者说数字系统中应用离散傅立叶变换,可以说是一大进步.傅立叶变换是线性系统分析的一个有力工具,它使我们能够定量地对图谱进行分析. 其通过在时域和频域来回切换图像,对图像的信息特征进行提取和分析,简化了计算工作量,被喻为描述图像信息的第二种语言,在频谱分析中得到广泛运用,不过在高分子材料领域的尝试还是很少.主要是因为和金属材料相比,高分子材料的力学特性使其要在受冲击的情况下输出频谱并不容易.并且在实验过程中冲击输入的传递函数也很难确定,因此涉及此方面的实验结果比较少.

    2 、实验流程及方法.

    从理论的观点看,用离散傅立叶算法解决复杂性问题已经达到了一定的成熟程度,而且快速傅立叶算法也发展得比较成熟了.但在实际应用中,FFT 算法的选择必须考虑到结构的复杂性和实现的难易程度.随着需求的发展,出现了多种其他的快速变换算法,如快速沃尔什变换、快速数论变换等,但与 FFT变换相比较都存在着一定的局限性.因此,在做材料冲击频谱的分析当中,FFT 也是这些方法中最可能被使用的,并可能是最好的方法.我们将利用计算机软件在计算机上实现 FFT.我们选择由美国 Mathworks研发的数学软件 MATLAB 进行 FFT 模拟和数值分析.

    实验原料方面需要找出一种韧性较强和一种脆性较强的材料,以它们的冲击试验频谱来进行对比,就能比较明显的发现它们在频谱中不同的特征,也就是说能够简单的在频谱的对比中看出材料力学性能的不同之处,那么用傅立叶变换的分析方法来对材料的结构进行表征的方法就能实质上可行.因此使用了聚丙烯 ( PP) 、聚乳酸 ( PLA) 两种物理性质截然不同的材料进行冲击试验.

    实验所用的冲击设备选用 JJ20 记忆式冲击试验机,相应的机器参数设置如图 1 所示,冲击试验条件选用美国标准( ASTM D256-2000) .
 

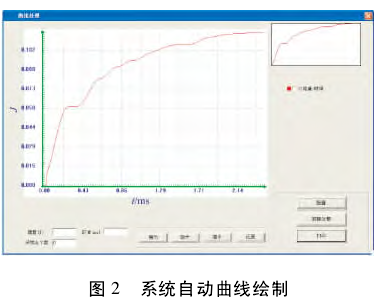
    点开始试验,将锤体拉下,实验开始,垂体落下后将样条打断,根据打断的实际情况选择破坏类型,实验完成后回到主界面,打开原始数据( 后缀名位 ZNF 的文件) ,点“曲线分析”,进行曲线绘制,如图 2 所示.
 

    再选择数据处理,最后将文件以 Excel 形式保存,JJ20 型记忆式冲击机可以将记录下来的数据以 Excel文件的形式保存到计算机中,因此可以使用 MATLAB与 Excel 的接口插件将 Excel 中的数据读入 MATLAB中进行处理.将 Excel 中的数据调入 MATLAB 后,可以利用MATLAB中的一些功能函数对数据进行分析处理.MATLAB 中使用快速傅立叶变换函数可以简单的对函数进行傅立叶变换,还有其他一系列函数可以帮助我们进行分析.

    我们主要使用到的函数如表 1 所示( 假设使用变量为 x) .
 

    3 、实验数据的处理.

    3. 1 、以 pp 为原料进行冲击所得到的部分冲击部分数据如表 2 所示.
 

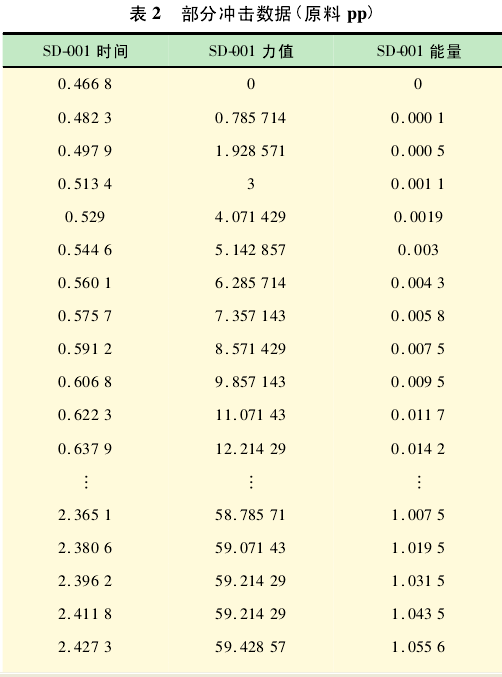
    其中,力值指的是该时刻摆垂所受到材料施加的反作用力.根据数据,将数据读入 MATLAB,设时间之为 t1,反作用力为 l1,进行如下操作:

    ( 1) 选中 128 个时间值,点击“putmatrix”,设名称为“t1”( 见图 3) .
 

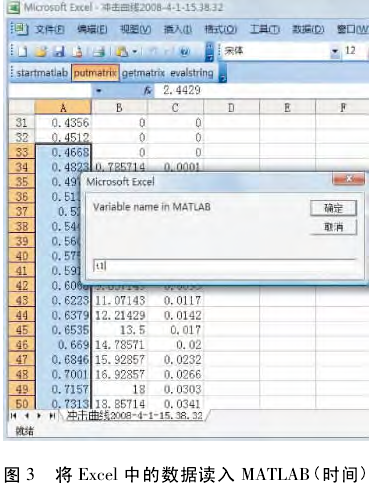
    ( 2) 选中 128 个反作用力值,点击“putmatrix”,设名称为“l1”( 见图 4)
 

    图 4 将 Excel 中的数据读入 MATLAB( 力值)这里选取 128 个原因是快速傅里叶变化的运算是针对 2N个数据进行运算的,虽然在数据不符合 2N个的时候会自动进行补 0,不过为了简化这部分,选择了128 个数据进行处理.

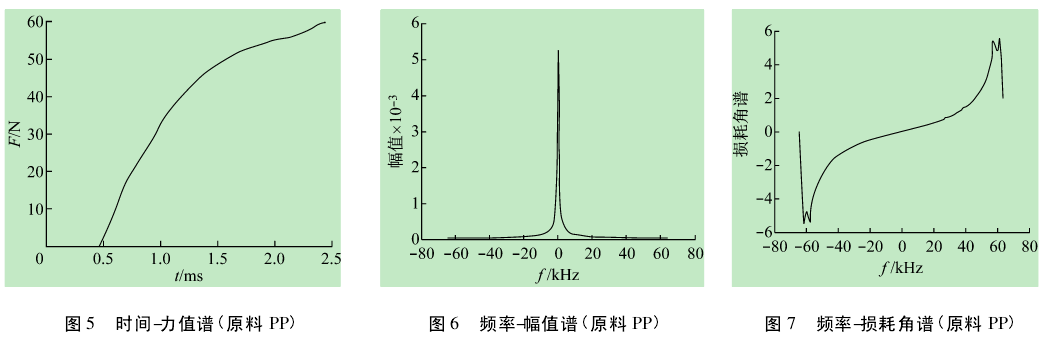
    ( 3) 在 MATLAB 命令窗口中键入“plot( t1,l1) ”,做出该样条的“时间-力值谱”,如图 5 所示.

    ( 4) 在 MATLAB 命令窗口中键入“f1 = fft( l1) ”,对谱线进行快速傅立叶变换,结果记为 f1.

    ( 5) 在 MATLAB 命令窗口中键入“N =128”.

    ( 6) 在 MATLAB 命令窗口中键入“f = - ( 1/0. 015 5) ∶ ( 2/0. 015 5) /N∶ ( 1/0. 0155) - ( 2 /0. 015 5) / N”获得频率如下所示:

    Columns 1 through 11- 64. 516 1 - 63. 508 1 - 62. 500 0- 61. 491 9 - 60. 483 9 - 59. 475 8- 58. 467 7 - 57. 459 7 - 56. 451 6- 55. 443 5 - 54. 435 5Columns 12 through 22- 53. 427 4 - 52. 419 4 - 51. 411 3- 50. 403 2 - 49. 395 2 - 48. 387 1- 47. 379 0 - 46. 371 0 - 45. 362 9- 44. 354 8 - 43. 346 8…Columns 111 through 12146. 371 0 47. 379 0 48. 387 1 49. 395 250. 403 2 51. 411 3 52. 419 4 53. 427 454. 435 5 55. 443 5 56. 451 6Columns 122 through 12857. 459 7 58. 467 7 59. 475 8 60. 483 961. 491 9 62. 500 0 63. 508 1f = - ( 1 /0. 015 5) ∶ ( 2 /0. 015 5) / N∶ ( 1 /0. 015 5)- ( 2 /0. 015 5) / N式中,( 1/0. 015 5) 是冲击实验中采集的最高频率,它有实验仪器决定,也就是采样时间间隔的倒数.采集的最低频率为总采集时间的倒数,它决定了频谱的宽度.而在绘制幅值谱的时候把最低频率考虑为从 0 开始.

    ( 7) 在 MATLAB 命令窗口中键入“plot( f,fftshift( abs( f1)  ”,画出频率-幅值谱如图 6 所示.

    ( 8) 在 MATLAB 命令窗口中键入“plot( f,tan( angle( f1)  ”,画出频率-损耗角谱,如图 7 所示.

    000.

    3. 2 PLA 材料冲击所得的谱数据处理方法与

    3. 1 方法相同.所得的时间-力值谱如图 8 所示.频率-幅值谱如图 9 所示.频率-损耗角谱如图 10 所示.

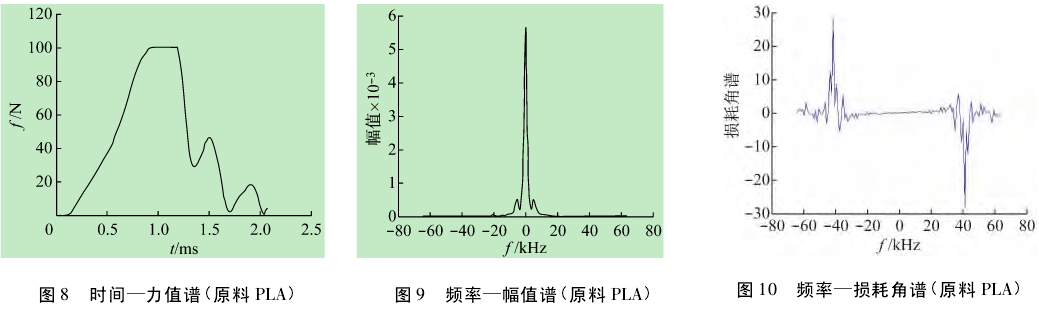
    从所得实验结果来看,时间-力值谱方面,我们对两种材料的简单了解,常温下 PP 属于韧性材料,而PLA 则更多的显示脆性这一特性.从两种材料的“时间-力值谱”中能看出它们力学性能上的显著不同,因为 PLA 的谱线力值增长很快,而且在 2 ms 的时候,已经被冲断,而 PP 则还未达到力值的最大值.这是因为在冲击的过程中,韧性较好的 PP 将摆垂的一部分冲击力吸收了,而 PLA 则几乎反弹了所有的冲击力.频率-幅值谱线方面通过观察 PP 和 PLA 频率-幅值谱,这对照的 2 个频谱我们知道它是关于 0 对称的,其实这源于快速傅里叶性质的对称性.我们选择右半部分进行观察,可以明显的发觉在频率等于 6KHz 左右的时候,PLA 比 PP 多了一个特性峰.说明脆性材料相对于韧性材料在此频率会多一个特性峰而非韧性材料一样是个几乎平滑的曲线.

    频率-损耗角谱方面通过观察 PP 和 PLA 频率-损耗角谱曲线可以发现,脆性材料相对于韧性材料在某些频率的时刻是瞬间变大,而且某个频率会瞬间出现一个更大峰值( 该脆性材料是在 40 kHz 左右这个频率出现一个最高峰,其损耗角几乎接近 30) .而韧性材料相对于脆性材料则比较平缓,缓缓上升,在一段频率范围内随着频率的增加,损耗角逐渐的增大,直到达到较大损耗角( 该韧性材料在 50 kHz 到 60 kHz 这个期间出现最大损耗,仅接近于 6) .

    4  实验结果与讨论.

    在实验的过程中,通过对冲击数据的分析,发现用傅立叶变换来分析材料的力学性质( 尤其是冲击性质) 是一种非常简便并且实用的方法.从傅立叶频谱的形状和数值中我们可以很简单的分析出几种材料在韧性、脆性上的不同.对于高分子材料这样一种典型的粘弹性材料来说,如果使用傅立叶变换来分析,就不难判断出材料的总体刚韧性质.虽然以目前的科技水平还没有研究出专门的傅立叶分析系统,但是这样一种方法一定能在不久的将来在材料分析( 尤其是高分子材料) 领域进行广泛的应用.现在已有的傅立叶红外分析等技术就是最好的证明.

    傅立叶分析从原理上讲是一种较复杂的数学分析,对任何数据进行傅立叶变换,都要进行大量的计算工作,这些工作不可能完全由人工完成[15].因此在对数据进行傅立叶变换是我们需要借助计算机来帮助进行计算工作.因此使用一些可以进行数学计算的软件是十分必要的.而 MATLAB 就是这样一种功能十分强大的软件.我们不仅可以利用软件中现有的函数很简单的通过套用函数的方法解决傅立叶变换的计算问题[16],还能通过 MATLAB 和 Excel 的接口很方便的从Excel 中直接调用我们的实验数据,不但为我们分析傅立叶频谱创造了有利的条件,而且给我们提供了一个强大的数据分析工具.

    此外,材料冲击试验是一个过程很短的实验,实验过程中我们需要收集材料在冲击过程中的受力数据,用这些数据画出材料的冲击谱线,因此一般的冲击试验机没有办法满足我们的要求.我们使用的是记忆式冲击试验机,它能够将冲击过程中所受到材料的反作用力记录下来,并已 Excel 数据表的形式输出,为我们解决了收集数据的问题,同时也通过 Excel 的数据形式和 MATLAB 相互连接起到数据转换的作用.

    参考文献( References) :

    [1] 张德震,杨全兴,王彬芳. 高分子科学教程[M]. 上海: 华东理工大学出版社,2001.

    [2] 洪定一 . 聚丙烯---原理、工艺与技术[M]. 北京: 中国石化出版社,2002.

    [3] 周达飞,唐颂超. 高分子材料成型加工[M]. 北京: 中国轻工业出版社,2005.

    [4] 许开宇,祝忠明,卢亚玲. 数字信号处理[M]. 北京: 电子工业出版社,2005.

    [5] 季 虎,夏胜平,郁文贤. 快速傅立叶变换算法概述[J]. 现代电子技术,2001,8: 11-14.JI Hu,XIA Sheng-ping ,YU Wen-xian. An Outline of the FastFourier Transform Algorithm[J]. Modern Electronic Technique,2001( 8) : 11-14.

    [6] 戴幻尧. 基于 matlab 的信号时频分析仿真[J]. 现代机械,2005( 5) : 1-3.DAI Huan-yao. Application and Study of M atlab on Time-frequency Analysis of Signal[J.]Modern Machinery Xandai Jixie,2005( 5) : 1-3.

    [7] 袁登科,陶生桂. MATLAB 中频谱分析单元的建模与应用[J].变频器世界,2005( 11) : 44-46.YUAN Deng-ke, TAO Sheng-gui. Modeling and Application ofSpectrum Analyzer Based on MATLAB [J]. THE WORLD OFINVERTERS,2005( 11) : 44-46.