
0 引言
"材料力学"是工科院校中一门重要的技术基础课,也是一门理论与实验相结合的课程。该课程对提高学生实践能力与创新能力具有极其重要的作用。材料力学实验部分在整个材料力学中具有重要地位,材料力学实验与材料力学理论教学互为支持,互为验证,通过实验可以加强对材料力学理论知识的理解。
弯曲变形是工程中构件的基本变形之一,如结构中的梁和板都是典型的受弯构件。梁的弯曲正应力计算公式是进行梁的强度计算的主要依据,该公式是建立在平截面假设的基础上,因此对该公式进行验证具有重要意义。目前,大部分高校都是通过开设弯曲实验课程,让学生通过实验数据验证弯曲正应力计算公式的正确性。这种方法有效,但却不能让学生直观的观察到梁截面上应力的分布情况。
为了提高学生的学习兴趣,同时增强学生的分析能力和创新能力,丰富教学内容和实验模式,本文在实验的基础上引入大型有限元分析软件 ANSYS,利用 ANSYS 软件绘制试件的变形图、应变图和应力图,并将 ANSYS 计算结果和实验结果、理论计算结果相比较,证实理论计算公式的正确性和应用范围。
1 弯曲实验
梁的弯曲实验示意图如图 1 所示,截面采用矩形截面,材料为低碳钢。
如图 1 所示矩形截面简支梁,截面大小为 12mm×24mm,梁的跨度为 820mm.分别在距梁端为 310mm 位置处施加集中力,荷载等级为 3 级,每级之间相差 60N.弹性模量 E=195GPa,屈服极限 σs=360MPa.根据外荷载在梁上产生的内力,梁被分为纯弯段(CD 段)和弯剪段(AC、BD段)。根据教材,梁的弯曲正应力计算公式建立在纯弯曲的前提下,因此,实验也主要测量纯弯段的应变和位移。在梁CD 段的侧面上,沿与轴线平行的不同高度的线段上粘贴有五个应变片作为工作片,另外在梁的右支座以外粘贴有一个应变片作为温度补偿片。分别位于中性层上、梁的上表面、梁的下表面,且应变片之间等距,取梁上表面位置为0,应变片位置分别在 0、6、12、18、24 高度处。将五个工作片和温度补偿片的引线以 1/4 桥形式分别接入 DH3818静态应变测试仪面板上的五个通道中,组成五个电桥。通过测试矩形截面梁在纯弯曲作用下横截面的正应力分布规律和转角、挠度,验证分析理论计算公式。当梁在载荷作用下发生弯曲变形时,工作片的电阻值将随着梁的变形而发生变化,通过 DH3818 静态应变测试仪可以分别测量出各对应位置的应变值。
该实验可采用增量法加载。每增加等量载荷 F=60N,测定各点在 0、60、120、180N 作用下的相应应变。取应变增量的平均值 Δε,依次求出各点的应力增量平均值。根据胡克定律有 Δδi 实=0.195Δε,并将其与理论公式得到的应力增量 Δδi 理=ΔMy/Iz相比较,来验证弯曲正应力公式的正确性,其中 ΔM=ΔPa/2.
2 ANSYS 分析
利用 ANSYS 软件,采用 BEAM189 单元建立梁的模型如图 2 所示,图 3、图 4 和图 5 是梁的变形图、应变图和应力图。图 6 和图 7 是通过第四强度理论得到的等效应变图和等效应力图。从等效应力图中可以清楚地看出:纯弯段梁截面上的正应力靠近中性层处趋近于 0,离中性层越远,数值越大,这证实了弯曲正应力与中性轴的距离成正比的分布规律。
此外,从应变图中可以直观看出,梁弯曲变形后纯弯段横截面仍然保持为一个平面,没有翘曲,这也说明了梁的纯弯段变形符合平截面假设。弯剪段横截面上除了有正应力外还有切应力,所以会引起纵截面的挤压,并且引起横截面翘曲。但当构件跨长与截面高度之比大于 5 时,可以忽略切应力的影响,所以图中弯剪段截面的翘曲不明显。弯曲正应力公式仍按照纯弯曲正应力计算公式计算。
以下是将 Δδi 实、Δδi 理、ANSYS 计算结果对比,如表 1所示。
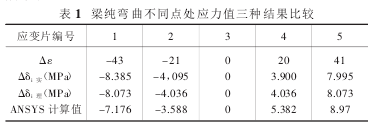
从表 1 可以看出,三种分析结果数值相近,说明实验分析、有限元分析和理论计算三者相统一,充分证明了理论公式的正确性。
3 结论
本文通过在传统的梁弯曲实验的教学中引入ANSYS 分析,使得分析结果大大增加可视性。学生可以通过应力图和应变图直观的看出其分布规律,增加了教学中的有趣性。从而提高学生的学习兴趣,增强学生的分析问题的能力。
通过将实验结果、理论计算结果和 ANSYS 分析结果对比,三者统一。充分证明了理论计算公式的正确性和实用性。该公式建立在构件纯弯曲变形下,且符合平截面假设。对于一般情况下的弯曲,即横力弯曲,虽然截面上的切应力对弯曲产生影响,但当构件的长度比截面高度大于 5时,可以忽略切应力的影响,弯曲正应力计算公式仍采用。
参考文献:
[1]孙训方。材料力学(1)[M].四版。高等教育出版社,2008.
[2]刘小妹,潘颖,等。ANSYS 在弯曲实验教学中的辅助作用[J].科学时代,2012(19)。
[3]浦广益,宋广雷。材料力学实验教学与有限元方法的有机结合[J].人力资源管理,2010(1)。