摘 要: 在生活中碰撞问题随处可见, 它同时也是物理学研究的主要对象[1]。本文通过数学建模以及编程计算分析了中子与原子核碰撞后的动能损失及碰后速度与散射角之间的关系, 发现了动能损失量随散射角度的增加而增大, 碰撞后的速度随散射角度的增加而减小。本文对微观碰撞问题的分析可以帮助中学生加深对碰撞和散射的理解, 以及深化对相关的概念 (如:动量定理、能量守恒定律等) 的认识[2]。
关键词: 弹性碰撞; 动能损失; 散射角;
1 引言
物理学中对碰撞问题的研究由来已久。根据碰撞前后的能量损失情况可以将碰撞问题分为三类:完全弹性碰撞、完全非弹性碰撞和非完全弹性碰撞[3]。宏观领域碰撞问题的研究可以帮助人们解决实际问题, 如对打桩、锻压、击球、撞车事故的研究可以更好的规避风险和事故的发生;在微观领域可以通过粒子的碰撞去研究物质结构和粒子间的相互作用[4], 如卢瑟福通过α粒子散射实验提出了原子内部的核式结构模型。
实际碰撞问题由于空气阻力、碰撞前后物体存在一定程度的形变、压缩阶段和恢复阶段时间短暂等因素, 研究起来比较困难[5]。本文从碰撞的理想化模型着手, 运用能量守恒定律与动量定理的相关知识, 研究了微观领域的中子与原子核散射的过程, 解决了散射过程中能量和速度如何变化的问题, 发现了动能变化量、碰撞前后速度变化量与散射角度之间的关系。

2 理论模型
如图1所示建立平面直角坐标系。设中子质量为m, 碰撞前速度为v0, 碰撞后的速度为v, 碰后速度v与x轴夹角为θ。原子核的质量为M, 碰撞后速度为V且速度与x轴夹角为准。
中子与原子核碰撞前的动能为:

根据机械能守恒定律, 碰撞前后能量不变:
图1
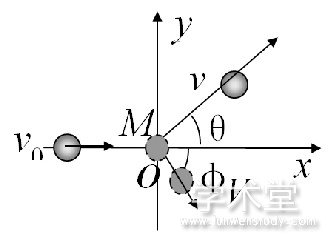
根据动量守恒定律, 碰撞前后沿着x、y轴方向动量方程:
由 (3) 、 (4) 得:

由 (5) 2+ (6) 2得:

由 (2) 得:
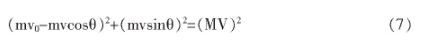
将 (8) 带入 (7) 得:
利用求根公式得两根, 舍去负数根, 所以:

所以中子损失的动能为:
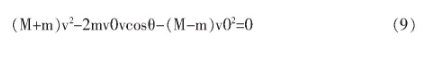
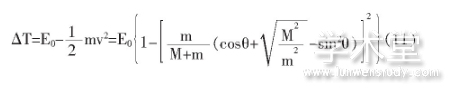
3 结论
3.1 理论分析
根据上文分析可得:
中子碰撞后速度越小, 动能损失越大。根据单调性可得当θ∈ (0, π) 时, (M2-m2sin2θ) , cosθ随着θ增大而减小;即它们随着θ单调递减。
可得当中子碰撞后的速度最小时, 损失的动能最大, 由于v随θ单调减小, 所以θ=π时v最小。
中子的最小速度为:

损失的最大动能为:
3.2 图像研究
图 (2) 中, x:散射角θ的度数,
y:散射前后中子的速度之比v/v0。
图2 中子与原子核作完全弹性碰撞的速度
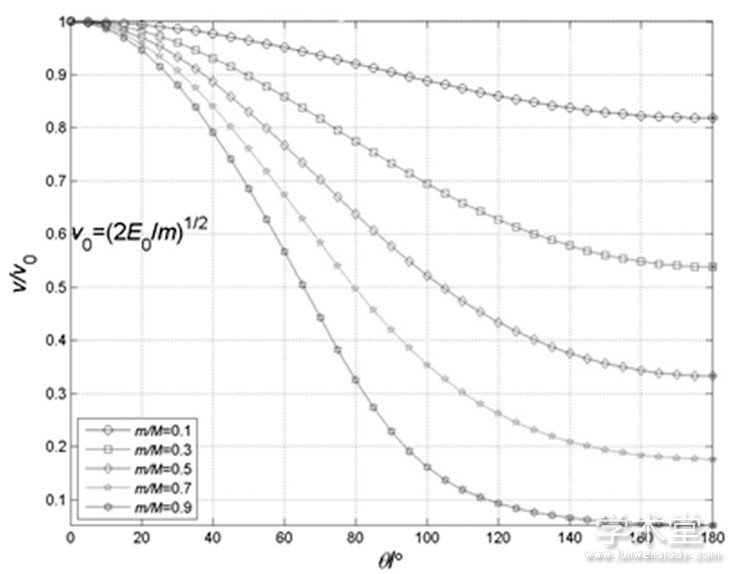
沿x轴方向来看, 各图像都呈下降趋势, 由此可得, 当原子核与中子质量比较为接近 (比值接近1) 时, 随着散射角度的不断增大, 中子速度不断减小;当散射角为π (即中子反弹) 时, 中子散射后的速率越小。
当我们向x轴做一条垂线, 不难看出中子与原子核质量越接近时, 对于同一个散射角, 散射速度就越小。
对于y轴方向, 我们不妨取散射角为20°时的曲线, 可以发现在所取得五组质量比值的曲线碰撞前后速度之比都有所下降。单取出质量比为0.9的曲线可以看出前后速度比值由1下降到了0.95左右。不妨认为在散射角为20°时每撞击一次速度之比减少0.05。由此可以推出撞击n次, 速度之比变为原来的 (0.95) n, 根据指数函数的规律不难发现, 当中子多次与质量相近的原子核碰撞后, 即使不反弹, 速率也会迅速减小直至不在运动。
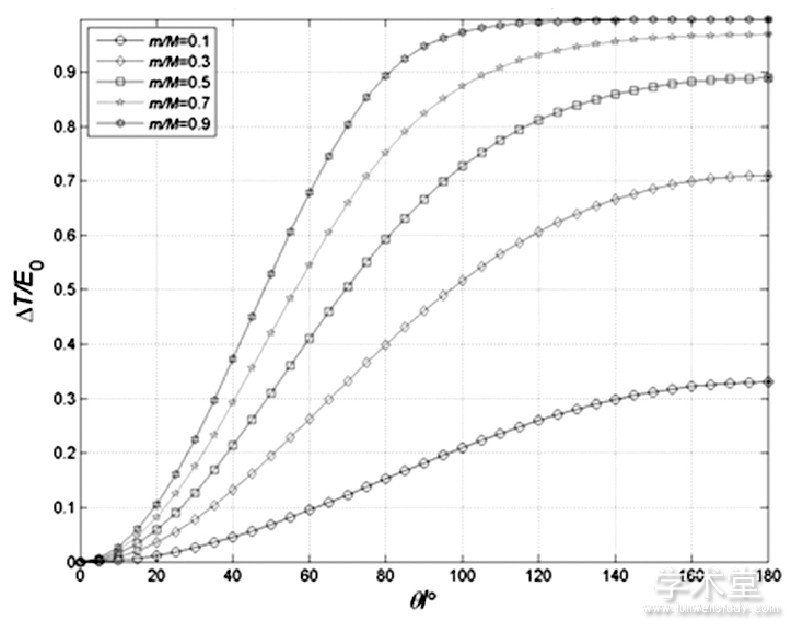
图 (3) 中, x:散射角θ的度数,
y:散射前后中子损失的动能与初始动能之比ΔT/E0
沿x轴来看各图像都呈上升趋势。由此可得, 当原子核与中子质量较为接近时, 中子散射后损失的动能随散射角的增加而增大;而当散射角为π (即中子反弹) 时, 损失的动能最多。
沿y轴来看:不妨取散射角为60°时的所有曲线, 可以看出中子的质量与原子核的质量越接近, 同一个散射角下损失的动能就越多。
4 研究展望
(1) 在建模的过程中, 中子与原子核的质量之比在0.1~1.0之间, 而在实际情境中中子与原子核的质量之比要小得多。本文并没有详细论证在其它情况下动能损失量与散射角的关系。可以利用编程, 通过画图来进行进一步的猜测与验证, 从得到的数据反过来优化模型。
图3 中子与原子核做完全弹性碰撞损失的动能
(2) 该模型仍存在很大的不足。在建模及运算的过程中, 一直认为中子与原子核做得对心碰撞, 而在实际问题中更为普遍的是非对心碰撞[6]。因此, 应进一步讨论在非对心碰撞时的动能[7]以及速度变化与散射角的关系。对于此问题已有解决办法, 进行正交分解后再次进行方程组的求解运算, 只是这时机械能不守恒, 方程的个数减少且未知数增加, 会加大计算的难度和误差。
(3) 对于完全弹性碰撞, 可以根据等能量守恒定律列出方程组求解。但如果进行的是非完全弹性碰撞前后动能就不再守恒。需要引入牛顿碰撞公式, 运用恢复系数求解[8], 这时模型需要重新建构, 而且要优化参数。
(4) 实际碰撞问题 (如车辆碰撞) 需要考虑很多外部因素的影响[9], 比如空气阻力、地面摩擦力、材料的杨氏模量、实际压缩和恢复阶段等。加入这些因素之后模型的适用性增强, 但可解性降低。会给后期的计算和程序编写带来很大的困难。
参考文献:
[1]葛松华, 王金成, 王泽华, 等.碰撞的能量转化和能量损失[J], 青岛大学学报, 2001, 13 (3) .
[2]岳巍巍.二次函数法分析对心碰撞[J].物理教学, 2016, 38 (2) .
[3]孙安媛, 黄沛天.也谈完全非弹性碰撞和恢复系数[J].大学物理, 2001, 20 (3) .
[4]于兴桓.完全非弹性碰撞中动能转化的六种形式[J].数理化学习 (高中版) .
[5]蒋小勤, 康颖, 秦国斌, 等.一维三体碰撞过程的数值实验研究[J].海军工程大学学报, 2005, 17 (1) .
[6]张绍兵, 王伟.一维弹性碰撞方程组解法的探讨[J].物理教学探讨, 2013, 31 (12) .
[7]张建, 李江, 倪行达.二维汽车碰撞模型病态性的处理[J].西南交通大学学报, 2007, 42 (4) .
[8]李忠相.处理斜碰问题的三种方法[J].物理通报, 2014, 5.
[9]朱欣顺.绕碰撞点转动的汽车二维碰撞速度分析[J].2006, 3 (2) .