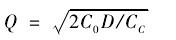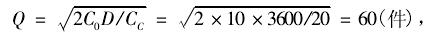6. 校内经营资源利用决策评价
在许多情况下,我们都可以把规划问题的决策变量看成是连续的变量。但在某些情况下,规划问题的决策变量必须是整数。例如完成某项工作所需要的人数或设备台数,某一机械设备的维修次数等。这就要求在原来线性规划的基础上加入新的约束条件,即要求某些变量或全部变量为整数,整数规划常用分枝定界法求解。
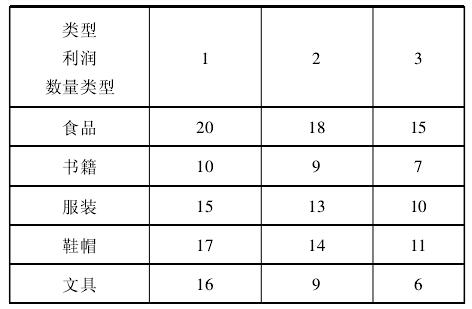
例 7:某民办高校校园内新建的1000 平方米的营业面积的商业中心计划自营,该中心希望将其营业面积分别用于食品、服装、鞋帽、文具和书籍五种类型的区域。每类区域的营业面积和允许的最少和最多的数量见下表:
每年每类商店可上缴的利润与每类商店的数量见下表:
试给出一整数规划模型使商业中心的利润最大。解:

7. 订货决策方案分析评价
在高校营运过程中,所需物资的供应与需求的数量和时间不一致的现象十分普遍,为解决这一问题,在供应和需求之间加上存贮这一环节,以协调供应和需求的矛盾。若以存贮为中心,将供应和需求对应于存贮的输入和输出,就得到了一个存贮控制系统。最基本的存贮模型包括六项费用:订货费用生产开工费、库存存贮费、缺货费、价格、生产成本。存贮模型除费用外,还有以下重要因素要考虑:(1)平均存贮。存贮费用中的库存存贮费与缺货费,都是按平均存贮量计算的。(2)需求。需求因素包括需求何时发生及需求量大小。(3)提前期。如果订货和到货之间的时间差不为零,为了在某一时刻得到补充,必须提前订货,提前的时间即为提前期。提前期包括从订货单发出至货物入库的全部时间,其长短必然会影响存贮量及存贮策略。设 D 表示确定时间内的需求量,Q表示每次订货量,C0表示每次订货费,CC表示单位商品存贮费,模型的目标是总费用最小,即订货费与存贮费之和最小,经典的经济订货批量模型为:
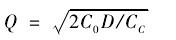
例 8:某民办高校因学生实验需要,每年实验室对某种备件的需求量为 3600 件,每订购一次商品,订货费为 10 元,每件商品的年库存存贮费为20 元。应如何订购,才能使年度(按 360 天计算)总费用最小? 解:
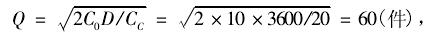

因此,最优订货策略是每次订购商品 60 件,订货间隔为 6 天,每年共订60 次,年度最小总费用为1200 元。
8. 不确定性经营决策方案的分析评价
不确定性决策是指决策者事先不知道决策可能出现的后果,或虽然知道可能的后果但不知道出现各种后果的概率的各种决策。对这种决策问题,方案选择的标准通常取决于决策者对未来所持的态度,不同的态度所选用的决策分析方法不同。
(1)审慎、稳健的决策分析方法,主要包括小中取大法和大中取小法。
小中取大法也称为悲观决策方法(瓦尔德决策准则),其思路是从各方案中选出最小的收益值,然后再从中选出收益值最大的方案作为决策方案。
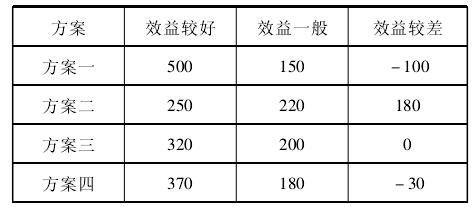
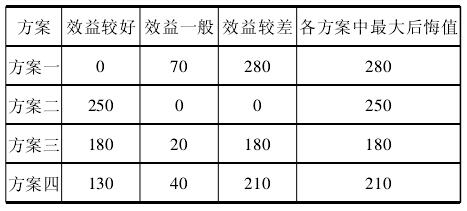
例 9:某民办高校超市为两层楼,现有四种经营方案供选择,分别是:方案一为自营,方案二为对外承包,方案三为一楼自营、二楼对外承包,方案四为二楼自营、一楼对外承包,每种方案学校获得的经济效益都有三种可能性,如下表(单位:万元):
首先找出各方案的最小收益值:方案一为 -100万元,方案二为 180 万元,方案三为0 元,方案四位- 30 万元,其次,以最小收益值为最大的方案作为最满意方案,因此,应选取方案二。这种做法是从最不利的情况下选择最满意的方案。
大中取小法,也称最小的最大后悔值决策法(萨凡奇决策准则),是从最不利的情况下选择后悔值即损失额最小的方案作为最满意方案。同上例,首先,找出不同状态下各个方案的最大收益值。效益较好时为:500 万元,效益一般时为220 万元,效益较差时为 180 万元。其次,计算在不同状态下各方案的后悔值(后悔值 =最大收益值 - 该方案的收益值),在效益最好的情况下,方案一的后悔值 =500 - 500 = 0,方案二的后悔值= 500 - 250 = 250 万元,方案三的后悔值 =500 - 320 = 180 万元,方案四的后悔值 = 500 - 370 = 130 万元。以同样的办法,可依次计算出效益一般、效益较差状态下的后悔值,如下表: