摘 要: 在线测评的内容是文字表述形式的定性评价,得到的结果往往是模糊难以量化的,不能达到科学评价的目的。文章通过对在线测评指标内容和测评因素分析,研究定性评价过程中可量化的要素,结合模糊数学理论,构建数字化的综合量化评价模型,设计综合评价分值表示形式,实现在线测评的量化结果应用。同时给出综合量化评价模型的计算机系统设定和分布实现的思路和方法,得出一种既可操作又评价科学的在线测评方案。
关键词: 测评; 量化评价; 构建与实现;
工作中常常会涉及到需要经过测评分析决策的事项,如党政机关的民主测评、教师教学质量的测评、学生工作满意度的测评等。随着科学技术的发展和信息系统的建设,为了提高测评参与深度和广度,并节约纸张等物资,测评工作逐步由现场投票转向网络投票的方式进行,而网络投票的形式大多数是对测评项目所设定的各项指标进行定性评价,具有较强的主观性,而测评参与者类型却各不相同,决定测评结果的要素模糊,难以量化,无法科学地对测评结果进行分析和使用。文章探讨一种在线测评量化评价模型,以实现科学评价的方案,并给出计算机实现的方法。
一、在线测评功能分析
日常开展的在线测评是组织根据工作需要,针对不同类型的被测评对象,设置不同类型级别的指标内容,一般分为一级指标内容和二级指标内容,各项测评指标的评价一般分为好、较好、一般、差四个等级,[1]所有测评内容会以电子表格的形式展示。参加测评人员可以在线登录,根据分配的测评权限,参照表格中指标内容对被测评对象逐一进行定性评价并提交,因此这样的测评结果具有模糊、主观、不确定、难量化的特点。此外,参加测评的人员根据职位岗位特点也会有所区别,为了综合体现被测评对象的测评结果,也会要求每类参加测评人员统计时所占的权重有所区别,并能根据需要对结果进行统计分析、筛选排序等。
二、量化评价模型构建
(一)评价内容可量化分析
在线测评大都是针对指标的定性评价,如何设计可量化的评价模型,在统一的模式下体现分数的相对公平,从而进行定量分析,显得十分重要。由于一级指标和二级指标内容各不相同,为了实现较为准确的量化评价,便于进行综合分析,需要把定性的评价转变为定量的分值,这里可以对各级指标按照评价的重要性赋以不同分值,并对指标评价的四个等级设定对应指标分值的比例系数,例如评价“好”“较好”“一般”“差”对应设定100%、75%、50%、25%的比例。而针对不同职位岗位的参评人员,也可以根据重要性设定不同的比例系数。考虑到实际在线测评中被测评对象和参加测评人员的数量、类型都会比较多,最终评价时需要综合考虑这些指标的分值和各类系数,可以考虑加权求平均的方法增加可比性。
(二)量化模型构建
1. 模糊数学理论
模糊理论是指用到了数学中模糊集合的基本概念或连续隶属度函数的理论,其中模糊数学是它的一个重要组成部分,广泛应用于评价和决策支持。而模糊数学是用准确的数学语言或算法来描述和处理模糊概念的一种数学方法。模糊理论是以模糊集合为基础,承认事物事实上存在的模糊性现象,以处理概念模糊不确定的事物为其研究目标,[2]用较为简单的解决模型,将模糊的事物量化成计算机可以处理的讯息,从而便于计算机进一步进行数据处理和分析。事物模糊性不同于随机性,事物的模糊性是指事物本身的概念是模糊难以确定的,而随机性是事物发生的条件变化引起的不确定的结果。
在线测评中,由于评价内容是文字表述的概念,是一条条定性的指标,具有明显的模糊性;而对指标的评价又是参评者的主观感觉,并不十分准确,也具有一定的模糊性。量化这些定性的评价结果,正是模糊数学的解决范畴,因此提出基于模糊数学理论的综合评分方法。
2. 量化模型设计
传统的模糊数学理论,考虑指标与评价结果的矩阵集,根据不同影响因素的系数运算,得出各评价等级对应的百分比,选择百分比最高的等级来确定评价的最终等级,[3]这在定性类型的测评中比较常用,但还无法进行排序和更深入的定量分析。笔者拟用准确公平的数字化方式,结合模糊数学理论解决测评结果定量分析和运用,实现对被测评对象的综合评分。
为了形成直观并清晰的测评结果,保证测评工作的公平性,实现量化比较,正如前面分析所设,对每级指标内容引入统一的分值系统,并对评价内容好、较好、一般、差四个等级对应相应指标分值的100%、75%、50%、25%,则每个被测评对象的最终测评评价设计如下面的量化模型:
设有限集合A={a1,a2,a3,a4,a5}是在线测评中一级指标分值集合,有限集合B={b1,b2,b3,?,b10}是在线测评中二级指标的分值集合,且一、二级指标及分值构成如下对应关系:
有限集合C={c1,c2,c3,?,c10}为评价二级指标内容得到的等级系数集,则C∈{1,0.75,0.5,0.25},由此可得出单个参加测评的人员评价某个被测评对象的总分值为:
假设在线测评中参加测评的人员类型有四种,定义有限集合D={d1,d2,d3,d4}为这4种不同类型的参加测评人员对应的权重系数分值,为了达到百分制结果,则d1+d2+d3+d4=1。定义有限集合N={n1,n2,n3,n4}为对应的每种类型的参加测评人员的数量,集合V={v1,v2,v3,v4}为每种类型参加测评人员对某一个被测评对象进行测评后的总分值的平均分,由上述设定可得
v2、v3、v4的取值以此类推。
于是得到某个被测评对象模糊综合评价分值如下:
基于此模型的综合评分方法,能够把定性的测评内容转换为定量的分值,提高了在线测评的可操作性,实现把定性评价转为定量评分的设想,体现公平性,且具有测评结果直观显示的优势,其结果的应用分析更加简单便捷。
三、量化评价功能实现
(一)数据库表中量化设定
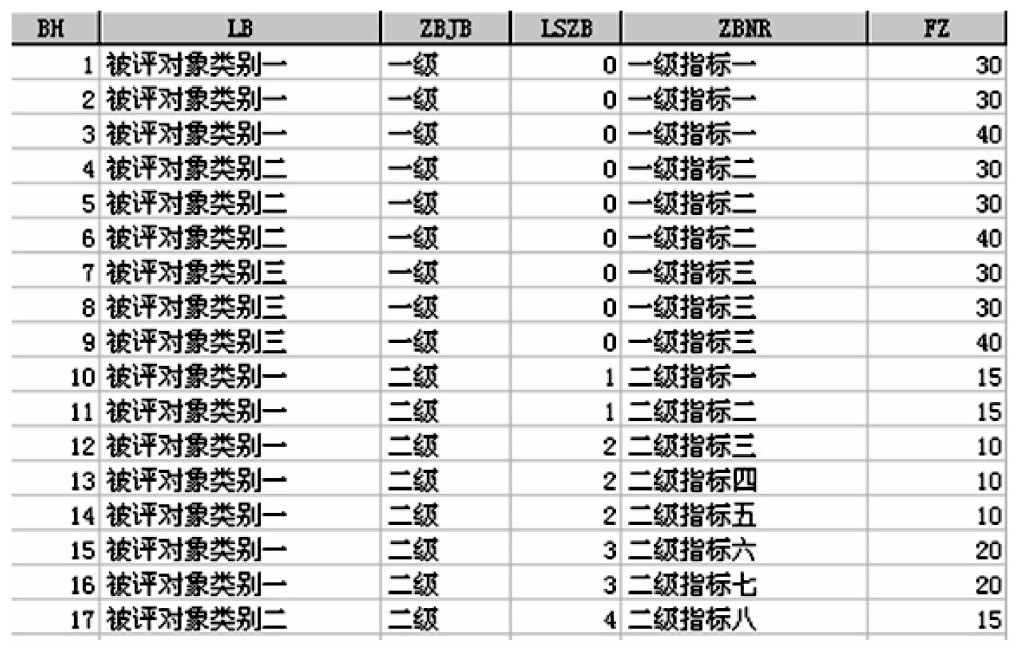
在线测评中被测评的对象可能有多种类型,每类被测评对象的侧重评价的指标和分值不尽相同,这就要求在线测评系统需设计多份测评表,并根据被测评对象的类型抽取不同的测评表。在此,假设被测评对象的类型有三种,在设计该系统数据库时,笔者专门设计三种不同类型指标的表格,根据指标重要性进行赋值,按对象类型进行存储。其表结构如图1所示:
图1 测评指标表结构
(二)量化评价模型的分步实现
在线测评中参加测评的人员类型有多种,且每种类型的参加测评人员根据需要设置不同的统计系数权重,有时还存在一个测评人员横跨两种参加测评类型的情况,即一个测评人员有两种身份,因而对量化评价分数的统计十分复杂。为了保证数据统计的准确性,笔者采取分步骤方式进行数据存储,然后再统计的方法。首先在测评阶段,对数据进行初步分类汇总存储,将各二级指标的评价分值按照一级指标的分类进行汇总存储,同时对参加测评人员进行对应不同被测评对象时的级别身份的转换,然后再对存储的数据按测评结果要求进行二次统计汇总。假设在线测评中有五项一级指标、两种被测评对象及三种参加测评人员为例,其实现的步骤如下:
第一步:将测评阶段的数据尽量详细的分表收集存储。
第二步:将收集的数据按类别进行平均分运算,并按身份系数要求进行结果统计和存储。
经过两次的数据存储和加工处理,可以实现在线测评中量化评价的综合评分方法,并可以在得分基础上进行多次数据处理,从而直观地得到测评所要的结果。这些实现步骤所涉及的思路和方法,可应用于多种在线测评系统中,具有通用性。
四、结论与展望
文章基于模糊数学理论扩展,利用定性评价转换为定量评分而构建的综合量化评价模型及其计算机实现方法已成功应用于某在线测评系统。经过多年的实际测评工作验证,该在线测评的应用,改进了工作方法,拓展了参与度,降低了组织费用,具有可操作性强、准确性高等特点,改变了传统评价结果模糊单一的弊端,有效提高了测评工作水平,实现量化分析的科学性,体现了测评工作的公平性,具有应用简单便捷的优势,成为评价决策支持的重要参考依据。同时,文章所建立的量化评价模型也为在模糊概念下进行在线测评提供了一种新的思路和途径。
参考文献
[1]周新邵.基于网络的湖南城市学院中层干部年度考核测评系统的设计与实现[J].电脑知识与技术,2018(14).
[2]周莉莉,陈善峰,李仁旺,刘海霞,应卫平.基于模糊综合评判的虚拟模特匹配算法[J].纺织学报,2007(9).
[3]林卉.基于模糊综合评价的高校民主评议党员测评方法研究[J].湖北工程学院学报,2018(3).