
1 问题分析与假设
NBA是全世界篮球迷们最钟爱的赛事之一,拥有30支球队,如何编制一个完整的、对各球队尽可能公平的赛程是一件非常复杂的事情.考虑赛程对球队的影响因素,将其转化为便于进行处理的数字格式,给出评价赛程利弊的数量指标,找出赛程对30支球队最有利和最不利的球队.若每支球队要进行82场比赛,需要考虑赛程以下几方面会影响球队的发挥:背靠背比赛的次数,82场比赛的分布情况,赛程安排的同步不同区赛三场对手实力等因素.
作如下假设:
1.统计某一球队82场比赛之间的时间间隔,以其标准差来衡量某一球队82场比赛的分布情况;
2.胜率是球队实力的真实体现;
3.忽略伤病、裁判、换帅或球员进步等人为因素和自然因素的影响.
2 模型的建立与计算
2.1模糊数学简介
对真实世界 模 糊 描 述 的 基 本 理 论 由LotfiZadeh在1965年提出,其框架的基本理论是经典集合论的直接推广.在一个经典集中,元素要么是集合的成员,要么不是.小于10的偶数的集合确切地包含4个元素{2,4,6,8}.从另一个角度来说,这个集合能被描述为一个定义于某个“论域”的隶属函数(membership function)mA(x)。
当变量x是集合A的元素时,函数取值为1;否则为0.一个模糊集(fuzzy set)提供了这样的可能性:除了{0,1}外,mA(x)还可以取其他的值,比如说[0,α]范围内的值,这个值表明了x隶属于A的程度.为了保持一致,通常将可能的取值范围按比例调整到0~1,包括0和1在内.隶属关系mA(x)=1表明元素x一定属于A,隶属关系mA(x)=0表明元素x一定不属于A,中间值则表明隶属的中间程度.正是这个中间范围体现了模糊集对于经典的“清晰”集的拓广.按照连续映射而不是一些(x,mA(x))取描述隶属函数往往更为方便.
2.2赛程利弊指标的模糊评价方法
在赛程利弊指标评价问题中,存在着许多不确定的因素,它们具有模糊性,利用模糊线性加权变换模型来解决该问题.符号说明:r:一球队在82场比赛中背靠背比赛的次数;s:一球队82场比赛之间的时间间隔的标准差;t:一球队与同部不同区赛三场的球队的平均实力.设R为模糊关系矩阵,W =(w1,w2,w3…,wn)为输入的模糊向量,B(b1,b2,…,bm)为输出的模糊向量.其中,(w1,w2,w3…,wn)为因素的权数,要求满足归一化条件【1】

2.3因素r的模糊评价隶属函数
背靠背比赛严重影响球队的体能,限制球队的发挥,NBA中规定每个赛季给一支球队定的背靠背上限是24对.根据该标准,定义背靠背次数的模糊评价隶属函数.【2】

2.4因素S的模糊评价隶属函数
若一段时期内比赛的安排过于密集,会使球员疲劳、球队比赛欲望下降.建立对一球队82场比赛之间的时间间隔标准差(用来衡量比赛的密集程度)的模糊评价隶属函数.假若比赛天数为169天,每支球队将在该期间内安排82场比赛.
最极端的情况是安排81场背靠背的比赛,另一场比赛与之的时间间隔为88天,此时的标准差为9.90.基于此,建立因素的模糊评价隶属函数μs(x)=9.9-x9.9.
2.5因素t的模糊评价隶属函数
每支球队与同区的每一球队赛4场(主客各两场),与不同部的每一支球队各赛2场(主客各一场),与同部不同区的每一球队有赛4场和赛3场(2主1客或2客1主)两种情况,每支球队的主客场数量相同且同部3个区的球队间保持均衡.一队与同部不同区赛3场的球队共4队,赛4场的球队共6队,不赛3场就要赛4场.因此,与之赛3场的4队平均实力越强,则其所有对手的平均实力越弱,对其越有利.一球队与同部不同区球队赛3场的对手的平均实力可以这样计算:t=a1+a2+a3+a44,其中,a1,a2,a3,a4是与之同部不同区球队赛3场的对手对应的胜率.建立t的模糊评价隶属函数μt(x)=x.
3 模型计算
3.1计算数据从新浪网查找NBA赛程安排表,使用函数计算得到表1的数据。【3】
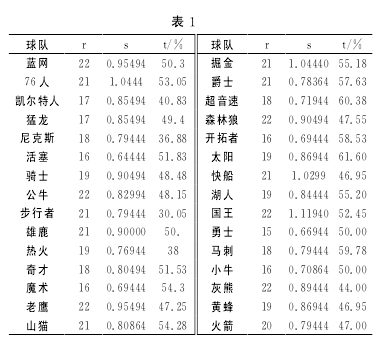
3.2计算结果【4】
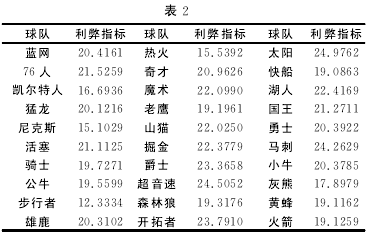
定义权系数为,根据表1的数据,使用模糊线性加权变换模型,利用matle数学软件计算出各球队的赛程利弊指标,见表2.利弊指标的数字越大,表明对球队越有利,利弊指标数字越小表示对球队越不利.
根据计算结果,可以给出各球队的利弊排名,见表3.【5】

从计算结果中可以发现,火箭队的赛程利弊指数为19.1259,赛程对其是相当不利的;而赛程对30支 球 队 最 有 利 的 是 太 阳 队,利 弊 指 数 为24.976 2;赛程对30支球队最不利的是步行者队,利弊指数为12.333 4.
从这个结果中可以看出,步行者队想要夺冠希望很小.
4 结论
提出了NBA赛程利弊数量指标的评价方法.通过参考专家意见和大量数据,使用模糊数学理论,应用模糊线性加权变换模型计算了30支球队的赛程利弊指标.该模型是较客观地评价各球队的赛程利弊.在模型中忽略了旅程的因素,相信还有一些较重要的因素(比如连续客场的场数等)在模型中未能体现.
参考文献
[1]Zadeh,L.A.Fuzzy Sets[J].Information and Control,1965,8:,338-352.
[2]Zadeh,L.A.Outline of a New Approach to the Analysis of Compex Systems and Decision Processes[J].IEEE Transactions on Sys-tems,Man,and Cybernetics,1973(1):28-44.
[3]蔡锁章.数学建模[M].北京:中国林业出版社,2003:1-30.
[4]吴值民.学生面试问题[J].数学的实践与认识,2007,37:14.
[5]赵文英,葛礼霞,廖飞.一族新的离散lax可积系统[J].牡丹江师范学院学报:自然科学版,2009(1):4-5.
[6]张格亮,李昕风.险投资项目评估中几种数学方法评析[J].牡丹江师范学院学报:自然科学版,2012(1):1-4.