
科学研究水平对于独立学院来说是一项重要的工作,为了鼓励教师的科研热情,学校各个类别的科研项目的立项评审工作也就成为了重中之重。而对于这项重要的工作我们往往忽略了其在工作方法上的弊端,是否考虑到其评审过程及其评审结果的客观性,因此我们需要探索更好的方法来应用到独立学院科研立项的评审工作当中去,那就是模糊数学的理论。模糊数学理论作为数学领域比较年轻的数学知识体系,广泛应用于解决各行各业复杂多变的实际问题。本文就是采用模糊数学的理论,探究在独立学院科研管理工作中,将模糊综合评判法应用到科研项目的评选上,针对项目评审过程中的某些特性,建立综合评价的数学模型,使独立学院科研项目的评审工作更加客观公正,从而提高了独立学院整体的科研水平。
一、在独立学院科研立项评审过程中应用模糊评判法的必要性
模糊数学概念是相对精确数学而言的,它是用数学的理论方法研究和解决现实中遇到的模糊现象的一种数学方法。模糊评判法是对人脑思维评判事物的方法进行模拟,恰当地描述这些模糊的概念,对其进行数学化和定量化。独立学院的科研立项的评审过程就是一个多元复杂的过程,因此引入模糊评判法可以大大提高项目评审的客观性。
(一)科学研究对象的模糊性
科学研究的对象涉及到科技、文化、社会众多既有交叉又各自独立的知识领域,这些因素都具有模糊的特性,所以很难比较不同领域的科学技术的先进与否和研究方法的好坏,这些评断之间的界限很难分清楚。
(二)评审专家思维的模糊性
科研项目的评审是需要评审专家进行评审的,需要用到大脑。人的大脑在对大量信息进行处理和加工的时候,其部分的评判结论具有模糊的特性,此种评判跟计算机给出的精确结果存在着很大的差异,人脑给出的是综合的介于某个范围内的评价结果,而计算机的结果是精确的不能再精确的数据,我们需要把人脑的模糊判断量化成具体的数据,加以比较,得出比较客观的评判结果。
(三)科学研究过程的模糊性
科学研究是个非常复杂的过程,需要计算项目投入的资本跟产出的效益之间的比例,这里面不仅包括投入的研究材料、研究人员,还包括投入的实验设备等,要考虑到每个环节的合理性、必要性和稳妥性,这期间就存在着诸多的不确定因素和比较多的过渡状态。
二、独立学院科研立项模糊综合评价数学模型的建立
目前独立学院的项目评审工作绝大多数采用的是组织专家评审委员会的形式,通过专家的讨论,投票评选出获得资助的项目及资助的等级。而科研立项的评审过程,实际是对研究内容的多种属性客观的认同过程,要考虑到各方面的因素,权衡评价结果的各个指标,得到客观的判断和综合的考虑。在科研项目评审时,评价一个项目的水平高低、质量优劣,大多数的情况下都属于模糊的评判概念,尤其是由于评委专家对行业领域知识的局限性。在项目评审的过程中,多数情况下不能用绝对的肯定和否定来表达结论,而是趋向于某个结果的评判,因此要引入模糊数学的理论来解决独立学院科研项目评审过程中存在的问题。
模糊综合评价数学模型是在模糊数学理论的基础上,把定量的数据跟模糊的标准做一下模糊变换和分配一定的权重,在这个基础上对评审对象进行模糊处理的一种评判手段。
(一)建立科研立项评价因素的指标集合
能够影响到科研项目评选工作的因素较多,我们需要多方考虑采用那些对评审结果影响比较大的因素作为评价指标,同时考虑到指标较少不能够全面体现评审结果的客观性,指标太多又不能突出某些因素的重要性。我们根据独立学院科研项目的特点及评审过程中评审专家考虑的几个重要方面选定5个指标构成科研立项评选的评价指标集合U,即U={u1·u2·u3·u4·u5},其中:u1为研究内容的必要性,u2为研究方法的创新性,u3为研究方案的可行性,u4为研究基础的扎实性,u5为解决问题的重要性。
(二)建立科研立项评价指标的评价等级集合
考虑到能够让评审专家将评审指标分成多个等级,且如果等级的个数较少不利于项目之间拉开档次,如果等级个数较多将导致评审结果比较分散,因此一般把评判的等级分为4个,由这四个等级构成评审等级集合V,即V={v1·v2·v3·v4},其中:v1为优秀,v2为良好,v3为一般,v4为差。
(三)构造模糊关系矩阵
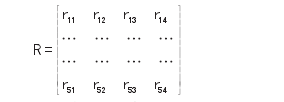
从U到V的模糊关系矩阵为:R=(rij),其中i=1,2,3,4,5;j=1,2,3,4 评审专家在评审会上通过详细阅读申请者上交的材料,综合考虑各个方面,通过对各个项目之间的比较,对参评项目的给出较客观的评审意见,根据项目申请书中的研究背景、研究内容、研究意义、研究方法等内容每个评委针对每一个评价指标给出其相应的评判等级,而且只允许给出一个等级,否则不生效。
当所有评委给出结果后,需要评委会秘书对数据进行统计,得到的模糊关系矩阵如下:【0】
(四)确定指标权重向量
通常情况下,评审指标在评审过程中对评审结果的影响程度各有不同,因此我们要根据其不同的影响程度赋予每一个指标不同的权重系数,以体现其不同的重要性,可以根据评审专家的经验来分配各个评审指标的权重,确定权重系数。如若设定的5个评审指标的权重系数为a1,a2,a3,a4,a5,且5i=1∑ai=1,则得出的权重向量为A=(a1·a2·a3·a4·a5)
(五)模糊综合评判
作为U上的模糊子集A,(U×V)上的模糊子集R,作模糊变换B=A·R,把它叫做综合评判。
在这里我们需要考虑一下B的运算方法,如果我们采用模糊矩阵的合成运算的方法进行运算,这种运算方法跟普通的矩阵运算乘法比起来具有简单容易计算的特性。但是它采用的是在相加的情况下选取各个项的最大者为和,在相乘的情况下选取每项中最小的因子为积,这样能在很大程度上减少“人情评判”的作用,但是会丢失很多重要的信息。因此,为了既客观又充分地反映每一个评审专家的想法,我们只能采取普通矩阵乘法的运算方法,也就是我们常说的加权平均法则,这种方法可以考虑到每个因素并且按照权重来分配份额。【1】

(六)评选标准的选定在B=(b1·b2·b3·b4)中,每个依据的影响力度不尽相同,为了区别,我们分别给b1·b2·b3·b4设定一个权重系数F.【2】
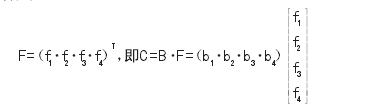
然后我们在计算后可以采用以下两个推导方式来对我们得到的这些数据加以分析。第一种方法是,我们事先可以制定一个固定的标准,即通过给定一个数D,接下来如果当C大于D的时候,我们就可以把项目列为资助项目。另一种方法是,我们可以把每个项目计算而得到的C值进行排序,然后按照资助项目个数和资助力度,最后根据它们的整体排序来划分项目的立项与否及其相应的立项等级。
三、结论
由于参与项目评审工作的主体是人,事实证明跟人关联的事情均具有及其复杂的特性,人们的评判比较难于用是非、对错来描述,因此项目的评审过程具有一定的模糊特性,针对在评审过程中大量的不确定因素,本文采用模糊数学的理论对项目的评审工作给予了客观的评判。基于这个模糊数学理论构建起来的数学模型,既能够考虑到独立学院科研项目评审工作的特殊性,又能够很好地尊重评审专家给出的评审结果。因为通过模糊评判法得出的评审结果是对项目整体的综合评价,较单独的评委投票得出的结果更具有客观性,而且在很大程度上打消了一些人认为项目评审过程中人为因素较多的疑虑。长此以往,这将有利于独立学院科研立项向更高的研究水平发展,能够使独立学院成为以教学取胜的特色学校,同时其科研能力也不容小觑。
参考文献:
[1]贺仲雄。模糊数学及其应用[M].天津科学技术出版社,1983.
[2]陈守煜。系统模糊决策论与应用[M].大连理工大学出版社,1994.