摘要:对雷诺数Re=1200条件下的圆柱在均匀来流中横向受迫振荡的尾流控制问题进行数值模拟分析。通过尾部加喷射气流对不同旋涡脱落模式进行尾流控制, 通过对圆柱在不同振幅和振荡频率下涡脱落情况进行观察研究, 最终在无量纲振荡频率feD/V=0.21, 振幅比A/D=0.5情况下发现了2S旋涡脱落模式并通过在柱体尾部施加不同速度的喷射气流对其进行控制;在feD/V∞=0.189, A/D=1.5情况下发现了P+S旋涡脱落模式并在柱体尾部施加不同速度的喷射气流对其进行控制。涡量图和功率频谱图结果表明, 在2S模式下, 喷射气流对旋涡脱落抑制效果明显, 尤其当喷射速度Ve=5m/s时效果显着。而在P+S模式下, 当喷射速度Ve=2.5m/s时旋涡脱落抑制效果较好, 而当喷射速度Ve分别为5m/s和7.5m/s时, 抑制效果一般。
关键词:尾流喷射; 旋涡脱落; 振荡柱体;
圆柱绕流是生活中一种极为常见的钝体绕流现象, 一百多年以来, 众多学者关注并开始研究这种现象的内在机理, 与此同时, 在这个基础上, 产生了大量的理论研究课题。奔腾的水流冲击桥墩, 高空中气流吹过飞机机翼, 烟囱中烟飘过房屋等生活中的现象, 都具有一定的柱体绕流机理。当发生这些情况时, 流体绕过圆柱体表面, 其边界层会产生分离, 当达到某个特定雷诺数范围内时, 将出现规律性的涡脱落模式, 随之激发交变载荷, 使柱体内部结构产生振动[1], 造成物体内部结构被破坏, 严重影响结构物的可靠性和安全性。涡脱振动在现实生活中已经产生了不少的破坏实例, 如1940年的美国塔科马大桥仅通车四月后便发生坍塌事件, 英国渡桥电厂冷却塔于1965年发生风毁事件等, 都是由于涡脱振动导致的灾难性事件。因此, 研究振荡柱体绕流特性, 并掌握其控制方法, 减弱甚至消除涡脱振动在工程应用上具有非凡的意义。
圆柱绕流一直是流体力学领域的学者们不断研究探索的重要课题, 而横向受迫振荡是其重要分支之一。1964年, Bishop&Hassan[2]通过圆柱受迫振荡实验, 对圆柱横向受迫振动的流动情况进行了分析, 测量了其波动阻力与升力。此后, 大量的学者开始研究其流场内部流动情况和内在机理, 得到了大量的成果, 如Sarpkaya[3]和williamson[4]等做出了细致的实验研究。Williamson[5]于2004年对横向振荡圆柱在定常流场中的尾流涡脱落模式进行了细致的总结, 他将涡脱落模式分为2S, 2P, P+S等模式, 其中S (single) 代表单个旋涡脱落, 2P (positive) 代表一对旋涡脱落。1995年Meneghini&Bearman[6]在雷诺数Re=200条件下, 通过对圆柱在不同振荡频率和不同振幅条件下的尾流现象进行观察研究, 找到了横向振荡圆柱尾流的涡脱频率与锁频现象, 并发现了频率大小范围。Koopman[7]在研究后发现, 当圆柱振荡的振幅小于某个临界值时, 锁频现象则会消失。Guilmineau等[8]使用数值模拟方法, 研究了二维圆柱在定常流场的自激振动绕流问题, 指出若初始条件发生变化, 则自激振荡系统会产生不同的激励, 在将上升速度作为起始条件时, 得到的振幅最大值与Khalak[9]的实验结果保持一致。
强迫振荡柱体绕流可以分为:横向振荡柱体绕流和流向振荡柱体绕流[10-11].研究发现, 大多斜向振荡柱体尾流的各种涡脱落模式在横向振荡和流向振荡中也可以发现, 而在一般柱体振荡中, 横向振荡作用远大于流向振荡, 其振幅相较于流向振荡大大增加。几十年来, 人们不断攻克柱体绕流领域中的各种难题, 得到了大量的成果, 在受迫振荡柱体尾流抑制方面, 程东旭和邵传平[12]采用数值模拟方法研究了雷诺数Re=200下, 尾部喷射对圆柱涡脱的抑制效果, 并找到了喷射速度的有效抑制范围;陈野军和邵传平[13]进行了尾部喷射对流向振荡圆柱的涡脱抑制实验, 发现了喷射速度的有效抑制范围, 并讨论了抑制范围随雷诺数变化规律, 但在横向振荡柱体尾流抑制方面, 并未取得太多成果, 尤其是利用尾流喷射抑制受迫振荡柱体涡脱落现象, 成果更是不多见。
为了抑制柱体尾流中的旋涡脱落, 同时减小阻力, 学者们研究出了一些控制方法, 主要分为主动控制和被动控制。主动控制就是通过向流场中注入能量, 使流场从绝对不稳定向对流不稳定转化, 从而使柱体尾流得到抑制。本文采用定常喷射作为控制方法来抑制尾流涡脱落。
在圆柱绕流的研究中, 实验无疑是一种重要的研究手段, 然而实验研究一般都是在近似条件下完成, 实验设备都难以满足所有的参数和定律, 因此实验研究也受到了不少的限制。近年来, 随着计算机技术的进步, 数值模拟以其计算费用低, 模拟复杂问题能力, 定量清晰描述流场的优点成为探索柱体绕流现象的一种新型有力手段。而在实际工程中, 普通的三维流场不仅需要考虑运动要素在三维空间的变化, 在方程求解方面也会遇到很多困难, 导致工作量过大;而在本文的数值研究中, 我们的实际实验在风洞中进行, 其模型为关于中心线轴对称的长方体, 在其Y方向 (垂直于截面方向) 上流体的温度分布和速度分布比较均匀, 因此可以通过研究流场中某个截面上的流动状态。来类比流场中其他截面的流动状态。除此以外, 不同于静止柱体, 振荡柱体随着振频增加, 其二维相关性随之增加, 因此可以将三维模型简化为二维模型。本文中笔者为了与后续的实验结果进行对比, 使用FLUENT软件, 对来流速度V=0.7m/s, Re=1 200的受迫振荡柱体在定常流场中的流动情况进行了数值仿真计算, 分析了在定常流场中横向受迫振荡圆柱绕流的两种不同又相互关联的涡脱落模式, 并通过在圆柱上沿轴线施加尾部喷射气流的方法研究了横向受迫圆柱绕流的不同涡脱落模式的控制效果。
1 数值方法
数值计算中涉及到的参数如表1.
表1 数值计算中的各种参数Table 1 Various parameters in numerical calculation
1.1 控制方程
本文研究Re=1 200时旋涡脱落的抑制情况, 采用二维非定常不可压Navier-Stokes方程作为其控制方程, 连续性方程和动量方程分别为:
式 (1~3) 中:u, v-x, y方向的速度分量;p-压力, υ-流体的运动粘性系数, ρ-流体的密度, 此处选择的流体为空气。
1.2 网格划分与边界条件
计算区域如图1, 为了保证流场充分发展, 采用大小为为80D×60D的计算区域, 圆柱与入口边界相距25D;与出口边界相距55D, 上游边界相距圆柱30D, 下游边界相距圆柱也为30D.取距离圆柱中心点一定距离作为运动区域, 这部分的网格采用动网格, 动网格区域:圆柱中心上下游各15D, 左边界距离圆柱中心6D.其他区域采用静止网格, 静止网格与动网格之间的临界面面采用滑移面 (interface) 分开。图1 (b) 为圆柱周围局部的网格分布方式。
流场速度入口为流域左端, 其大小为0.7m/s;右端为自由流出边界;上下界面采用滑移固体边界条件 (V=V∞) ;圆柱采用无滑移固体边界条件。
图1 网格划分Figure 1 Meshing Division
2 计算结果及分析
本文中雷诺数固定为1 200, 圆柱尾部喷射缝隙宽度为1mm.
2.1 网格无关性验证
为检验网格无关性, 采用网格Ⅰ、网格Ⅱ、网格Ⅲ、网格Ⅳ、网格Ⅴ五种不同密度的网格来分别计算Re=850时静止柱体在均匀定常流中的参数, 比较其斯托哈尔数 (St) 和阻力系数 (Cd) , 相应的网格参数见表2.从表2可以看出当网格从网格Ⅲ加密为网格Ⅳ时, St变化率仅为0.05%, 而网格Ⅳ再次加密后, 变化率基本保持不变, 表明网格Ⅲ可以满足计算需求。从表3可以看出, 网格Ⅲ计算得到St比其他两个人更接近实验值, Cd介于它们中间。
表2 网格模型参数及计算得到的St和Cd Table 2 Paramenters of five different grids configuration and computed St and Cd
表3 MeshⅢ计算所得斯特劳哈尔数对比Table 3 St number contrast with others
2.2 涡脱落模式为2S时的情况
在研究2S模式时, 我们选用A/D=0.5, fe=3作为典型工况, 采用喷射速度Ve=2.5m/s, 5m/s, 7.5m/s的喷气对其进行控制研究。
从图2 (a) 我们可以看到, 在未采用喷气时, 在每1/2振荡周期内有一个漩涡从柱体上脱落下来, 其类似于正常卡门涡街, 但两列旋涡的上下间距有时很小, 接近于单列涡串。从图2 (c) 可以看出, 当加入喷射速度为5m/s的喷气后, 几乎将漩涡完全消除, 通过观察动画, 我们发现, 当Ve=2.5m/s时, 漩涡大小较未控制时大大减小, 数量也减少很多, 同时一些残存的小的尾涡相比于无控制时向水平中心靠近, 喷气的能量在很大程度上抑制了涡街的形成。
图2 2S模式下未加喷射及加喷射后的涡量Figure 2 Vorticity chart of blowing added and without blowing in 2Smode
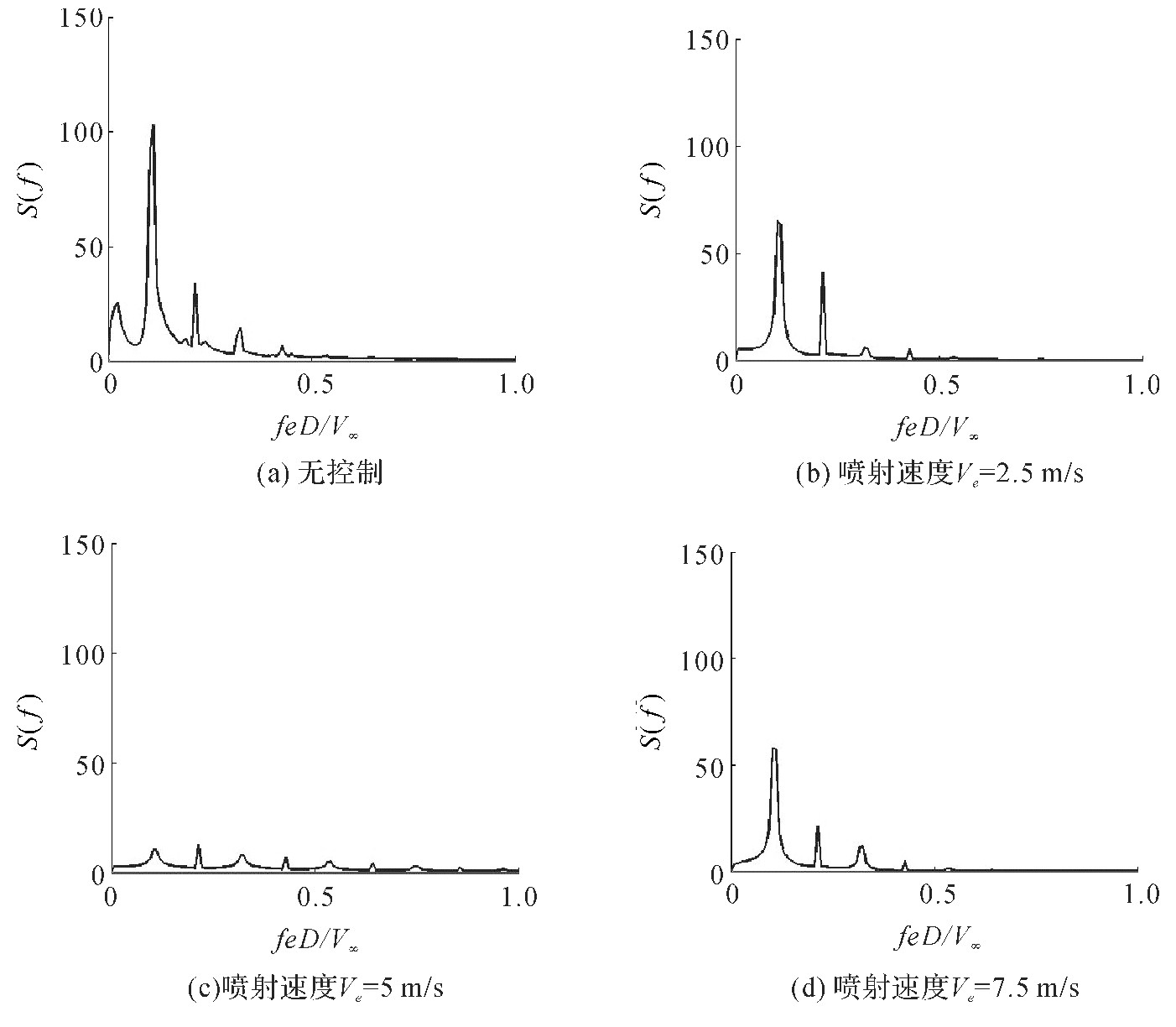
图3为在未加喷气时和喷气喷射速度分别为2.5m/s, 5m/s和7.5m/s时的频谱分析图, 观察图3中可以看出, 在加喷射速度后, 旋涡的能量得到显着的减弱, 分别减小到原来的1/5, 1/2, 1/3, 说明喷气对涡脱落的抑制具备一定的控制效果, 尤其是当喷射速度Ve=5 m/s时, 旋涡能量有大幅度的减弱;而当喷射速度Ve=2.5m/s时, 旋涡能量有小幅度的减小, 而当喷射速度增大为7.5m/s时, 相比较于Ve=5m/s时, 旋涡抑制幅度减小, 说明在喷射速度由5m/s增大到7.5m/s的过程中, 喷气对旋涡抑制作用在减小。
图3 2S模式下未加喷气及加喷气后的功率谱图Figure 3 Velocity power spectrum of blowing added and without blowing in 2Smode
2.3 涡脱落模式为P+S时的情况
在研究P+S模式时, 我们选用A/D=0.75, fe=4.33作为典型工况, 采用喷射速度Ve=2.5m/s, 5m/s, 7.5m/s的喷气对其进行控制研究。
通过观察图4 (a) , 可以发现, 当柱体处于无控制时, 在柱体的单个振荡周期内, 柱体一侧有一对反向旋转的旋涡脱落下来, 在另一侧, 有单个旋涡脱落下来, 其单涡或对涡的位置是随机的, 但可以观察到, 对涡一侧的能量明显大于单涡一侧的能量。当加入喷射速度为2.5m/s的喷气后, 流域内上下侧旋涡数量明显减少, 破坏了原本的P+S涡脱落模式, 从图4 (b) 上看, 被破坏后的涡在尾流中心线形成了一列单涡, 相比于无控制时向水平中心靠近, 喷气的能量在很大程度上抑制了涡街的形成。而在加入喷射速度为5m/s和7.5m/s的喷气后, 可以观察到, 原本的P+S模式受到影响, 在柱体原本产生的对涡转变为单涡, 而涡脱落模式也由原来的P+S模式转变为2S模式。当施加尾部喷射后, 形成射流, 近尾流内的速度高于来流速度, 使速度剖面发生改变, 改变了稳定特性, 从而使柱体振荡信号衰减, 在下游形不成规则漩涡脱落。
图5为P+S模式的频谱分析图, 图中可以看到, 相比于未加喷射时, 加喷射后, 旋涡能量有明显减弱, 功率谱峰值分别减小到1/10, 1/3, 2/3, 表明在该模式下, 喷气对旋涡脱落有控制效果, 且当喷射速度超过某一临界点后, 随着喷射速度的增加, 控制效果反而减弱。同流动显示对比可知:加喷气后, 旋涡能量减小, 涡脱落模式发生改变。
3 小结
本文采用数值模拟方法对Re=1 200的流场中大幅横向受迫振荡圆柱尾流控制进行研究, 通过采用施加尾部喷射气流的方法来抑制旋涡脱落。通过研究发现:
1) 圆柱的涡脱落模式会受振荡频率和振幅影响, 随着振荡频率和振幅的变化, 涡脱落模式也随之变化, 主要出现2S、P+S和2P等涡脱落模式。
2) 在2S模式下, 通过观察涡量图和功率谱分析, 喷射速度Ve=5m/s时, 尾流控制效果最佳;而喷射速度为Ve=2.5m/s、7.5m/s时, 也具备一定的控制效果。
图4 P+S模式下未加喷气和加喷气后的涡量图Figure 4 Vorticity chart of blowing added and without blowing in 2Smode
图5 P+S模式下未加喷射和加喷射后功率频谱图Figure 5 Velocity power spectrum of blowing added and without blowing in P+S mode
3) 在P+S模式下, 通过观察涡量图和功率频谱图, 当喷射速度Ve=2.5m/s时, 尾流控制效果明显;而当喷射速度增加到5m/s和7.5 m/s后, 尾流控制效果一般。
参考文献
[1]WILLIAMSON C H K, GOVARDHAN R.Vortex-induced vibration[J].Annual Review of Fluid Mechanics, 2004, 36:413-455.
[2]BISHOP R E D, HASAN A Y.The lift and drag forces on a circular oscillating in a flowing fluid[J].Philosophical Transactions of the Royal Society of london, 1964, 277:51-75.
[3]SARPKAYA T.Vortex-induced oscillations:a selective review[J].Journal of Applied Mechanics, 1979, 46 (2) :241-258.
[4]GOVARDHAN R, WALLIAMSON C H K.Vortex-induced motions of a tethered sphere[J].Journal of Wind Engineering&Industrial Aerodynamics, 1997, 69-71:375-385.
[5]WILLIAMSON C H K, ROSHKO A.Vortex formation in the wake of an oscillating cylinder[J].Journal of Fluid and Structures, 1988, 2 (4) :355-381.
[6]MENEGHINI J R, BEARMAN P W.Numerical simulation of high amplitude oscillatory flow about a circular cylinder[J].Journal of fluids and Structures, 1995, 9:435-455.
[7]KOOPMAN G H.The vortex wakes of vibrating cylinders at low Reynolds numbers[J].Journal Fluids Mechanics, 1967, 28:501-512.
[8]GUILMINEAU E, QUEUTEY P.A numerical simulation of vortex formation from an oscillating circular cylinder[J].Journal of Fluids and Structures, 2002, 16 (6) :773-794.
[9]KHALAK A, WILLIAMSON C H K.Fluid forces and dynamics of a hydroelastic structure with very low mass and damping[J].Fluids Struct, 1997, 11:973-982.
[10]ONGOREN A, ROCKWELL D.Flow structure from an oscillating cylinder:Part 1 Mechanisms of phase shift and recovery in the near wake[J].Journal of Fluid Mechanics, 1988, 191:197-223.
[11]ONGOREN A, ROCKWELL D.Flow structure from an oscillating cylinder:Part 2 Mode competition in the near wake[J].Journal of Fluid Mechanics, 1988, 191:225-245.
[12]程东旭, 邵传平。喷射方法对尾流旋涡脱落的抑制[J].中国计量学院学报, 2014, 25 (4) :398-403.CHENG D X, SHAO C P.Suppression of vortex shedding behind a cylinder by base blowing[J].Journal of China U-niversity of Metrology, 2014, 25 (4) :398-403.
[13]陈野军, 邵传平。尾部喷射对流向振荡柱体尾流旋涡脱落的抑制[J].中国科学:物理学力学天文学, 2012, 42:406-420.CHEN Y J, SHAO C P.Suppression of vortex shedding from an oscillating cylinder by base blowing[J].SCIEN-TIA SINICA Physica, Mechanica&Astronomica, 2012, 42:406-420.