摘 要: 斯托克斯定律是大学物理中流体力学部分的重点,同时在各个领域应用广泛。本文通过介绍了几种斯托克斯定律的应用,加深学生在学习过程中对该定律的理解和掌握。
关键词: 斯托克斯定律; 大学物理; 沉降速度;
Abstract: Stokes law is important in fluid mechanics of College Physics, and it is widely used in various fields. This paper introduced the application of Stokes laws to deepen students' understanding and mastery of the law during the process of learning.
Keyword: Stokes law; Subsidence speed; College physics;
斯托克斯定律是流体力学中的一个重要定律,而流体力学是大学物理教学中的重点知识。本文从不同方面介绍了斯托克斯定律的应用,以加深学生对斯托克斯定律的理解,提高学生应用知识解决实际问题的能力[1]。

一、斯托克斯定律
实际的液体都具有不同程度的粘滞性,当粘性流体做层流时,相邻两层之间存在速度差,层与层之间存在着摩擦力。当物体在粘性流体中运动的时候,物体的表面附着一层流体,我们称为附着层。附着层与相邻层之间的摩擦力,使得物体在运动的过程中需要克服这一阻力。如果物体是体积较小的球形,在层流速度较小的流体中运动的时候,球体所受的粘滞阻力可用斯托克斯定律来描述[2]。1851年,英国数学家和物理学家斯托克斯发现了能够描述这一阻力的公式,我们称之为斯托克斯定律:

(1)式中η是流体的粘度系数,v是小球相对于流体的运动速度,r是小球的球体半径。(1)式也称为斯托克斯公式,利用它可以计算小球在粘性流体中运动的沉降速度、测定流体黏度以及微小的球形颗粒半径等。
二、斯托克斯定律的应用
(一)沉降速度
假设有一个小球在粘性流体中下沉,此时小球收到了三个力:竖直向下的重力G、竖直向上的浮力F和流体的粘性阻力f。小球刚开始下落的时候,重力大于浮力,球体做加速运动。随着下沉速度越来越快,小球所受的粘滞阻力随着速度增大。当速度增大到某个值时,重力、浮力和粘性阻力三个力平衡,接着小球开始做匀速直线运动。此时,小球的速度我们通常称之为收尾速度或者沉降速度。若ρ为小球的密度,σ为粘性流体的密度。小球所受的重力可以表示为,所受的浮力为,粘性阻力为,当小球达到沉降速度时,我们根据受力分析可得

整理上式可得
由式(2)可知,当球形物体(如空气中的小雨滴、粘性液体中的细胞或胶体颗粒等)在粘性流体中沉降时,沉降速度与球体和流体的密度差、球体半径以及重力加速度成正比,与流体的黏度成反比。对于半径很小的颗粒,我们可以通过离心机旋转来提高颗粒受到的有效加速度,来加快它的沉降速度。医学中,在血常规的化验中测量红细胞在血液中沉降速度来检测身体的健康情况。血液是由红细胞和血浆组成的悬浮液,当把获取的血液样本放进竖直的血沉管内时,红细胞会在血浆中发生沉降,从而求得红细胞的沉降速度,在医学上也称之为血沉。若沉降速度过快,则有风湿、结核、肿瘤等风险。
(二)沙里淘金
黄金的化学性质稳定,一般不与其他物质发生化学作用,通常以游离态存在于岩石或沙石中。在自然风化的作用下,岩石破碎形成沙子与土,而黄金就埋藏在沙土中。为了把黄金与沙粒分开,经常使用的办法就是用水冲走沙粒留下了黄金颗粒。我们来思考一个问题,为什么水流能够把沙子带走留下黄金呢?我们可以用(2)式的沉降速度来描述这个问题[3]。由式(2)我们可以得知,对于半径相同的颗粒,密度越大沉降速度就越大。黄金的密度比沙子的密度大,所以黄金颗粒的沉降速度比沙子大。若用水流冲洗金沙混合颗粒,沙子和黄金同时发生沉降,黄金颗粒的沉降速度要大,所以先沉底,即下层是黄金上层是沙子。这时,再加以水平方向的水力冲洗,就将上层的沙子冲走留下了下层的黄金颗粒。同时,根据(2)式也可以得知,对于密度相同的颗粒,半径越大沉降速度越快,可见沙里淘金时下层的黄金体积分布为下大上小。
(三)密立根油滴实验
图1
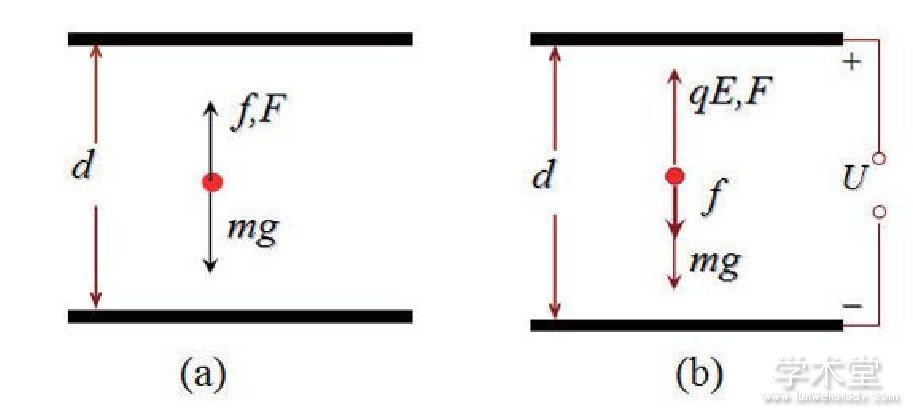
1911年,美国物理学家密立根用斯托克斯定律在油滴实验中证明了电荷量子化。如图1(a)所示,一个质量为m带电量为q的油滴处在二块平行板之间,在平行板未加电压时,油滴受重力的作用而加速下降,由于空气阻力f的作用,下降一段距离后,油滴以沉降速度vg匀速运动,此时油滴受力平衡。由斯托克斯定律知,受力平衡条件为:
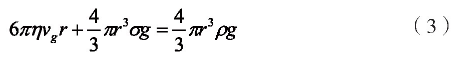
其中ρ为油滴的密度,σ为空气的密度,r为油滴的半径。然后在平行板上加电压U,如图1(b)所示,油滴处在场强为E的静电场中,其所受静电场力qE与重力方向相反。当静电场力大于重力时,油滴加速上升,由于油滴受到阻力的作用,上升一段距离后,将以ve的速度匀速上升,可得

联立(3)(4)式可得
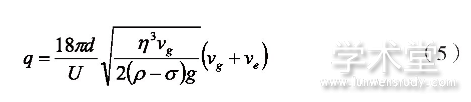
根据(5)式,若已知或能够测得极板电压U和距离d、油滴密度ρ和空气密度σ、空气的粘滞系数η、以及速度vg和ve,我们就可以计算出油滴的带电量q。密立根发现测得的电量总是某基本值的整数倍,测得电子电荷为(1.601±0.002)×10-19C,从而获得了1923年的诺贝尔物理学奖。
(四)解决混浊饮料的分层问题
随着社会的发展,人们的生活水平逐渐提高,营养丰富分新型饮料越来越受到人们的喜欢,例如酸奶及酸奶饮料、果蔬汁、花生奶等,这些饮料除了水分的存在还包含了一定的固相成分,外观不透明,我们通常称之为混浊饮料。这种饮料中通常存在悬浮的微小颗粒,避免在饮料生产过程中的沉淀和分层现象是关键技术,我们可以通过斯托克斯定律解决问题[4]。混浊饮料中的悬浮颗粒在饮料中存在的稳定性的考虑,可以类比为球形微粒在层流粘性流体中的沉降过程。根据(2)式可知,要保证混浊饮料不发生沉淀,关键问题是能够使得颗粒的沉降速度等于0。观察(2)式可得,需使得球体的密度等于粘性流体的密度。但是混浊型饮料在生产过程中,考虑到口味和口感问题,一般很难实现两种密度相等。根据沉降速度与颗粒半径的平方成正比,与流体的黏度成反比的关系,可以调节不同的参数来实现饮料不分层不沉淀的目的,比如调整饮料溶液和颗粒的密度差,减小颗粒直径,增大液体黏度等方法改进工艺。
(五)测量液体黏度
图2[5]
![图2[5]](http://www.xueshut.com/uploads/allimg/191031/36-191031150S41Z.jpg)
根据推出的沉降速度公式(2)可知,如果能够测得小球的沉降速度,一直小球的密度和粘性流体的密度,我们就可以计算出粘性流体的黏度η。以测量蓖麻油的黏度为例,我们简单介绍一下实验原理和过程。在实验室中经常利用落球法测量粘度系数[6,7],如图2所示,首先需要保证玻璃管的垂直,保证小球的下落路线沿铅直方向。其次,在蓖麻油的中选择一段,标注为L。L需标注在小球做匀速运动时经过的路程之内。用镊子夹起小球在油中浸润之后让其自由下落,用秒表测量小球经过路程L所用的时间,多次测量取平均值即可得到小球在蓖麻油中的沉降速度。代入公式(2)中可得蓖麻油的黏度。
三、总结
本文通过列举了不同领域中斯托克斯定律的应用,加深学生对该定律的掌握和理解,为提高学生的学习兴趣和大学物理的课堂教学质量提供一定的参考。
参考文献
[1]白璐,吴振森.多层面分层次大学物理教学改革[J].物理与工程,2010,20(6):43-45.
[2]张庆国,陈庆东.普通物理学[M].中国农业出版社,2011.
[3]司德平.雨滴的终极速度与沙里淘金[J].中学物理教学参考,2003,32(11):17-18.
[4]郑其良,钱志伟.斯托克斯(Stokes)定律在混浊型饮料中的应用[J].饮料工业,1998,1(1):24-26.
[5]毛爱华,武娥,蔡禄.落球法测液体粘滞系数的不确定度推算[J].大学物理实验,2018,31(3):101-104.
[6]唐果书.落球法测液体粘滞系数实验的研究[J].安徽教育学院学报,2006,24(3):22-24.
[7]庞学霞,段书兴,李霞,等.初速度对测定黏滞系数的影响[J].物理通报,2006,6:42-44.