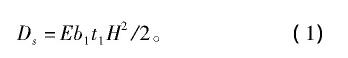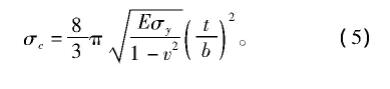高强度轻质铝制蜂巢结构的力学性能研究

材料力学论文第五篇：高强度轻质铝制蜂巢结构的力学性能研究

 

　　摘要：蜂巢夹层结构材料因具有高强度、轻质量的优势正在逐渐取代传统的结构材料, 并广泛地应用于汽车、船舶以及航空航天领域。然而, 这种材料在制造过程中生产工艺比较复杂, 特别是针对具有不规则断面的蜂巢结构, 容易在弯曲、切削等二次加工时出现制造上的缺陷和损伤, 从而影响结构本身的力学性能。为避免二次加工, 文章利用折纸技术的原理, 设计并制作了2种蜂巢结构试样。通过弯曲和压缩性能测试, 研究了蜂巢结构的变形行为和力学性能。在室温下获得的载荷-位移曲线表明, 变形过程大致分为线弹性、塑性平台和致密化3个区域。实验结果表明:蜂巢结构的弯曲刚度和抗压强度分别约为0. 32 k N·m2和0. 39 MPa;揭示了基于折纸技术制造的蜂巢结构具有良好的力学性能。

 

　　关键词：折纸技术; 蜂巢结构; 铝爪固定; 弯曲性能; 压缩性能;

 

　　Mechanical Properties of Honeycomb Structures Fabricated Based on Origami Technology

 

　　WANG Lijun SAITO Kazuya

 

　　School of Materials Science and Engineering, Xihua University The University of Tokyo

 

　　Abstract：Honeycomb sandwich structure with high strength and light weight is increasing being used to replace traditional materials, which is widely applied in automotive, shipping and aerospace fields. However, because its production process is very complicated, especially for the honeycomb structure with irregular sections, it is easy to appear defects and damages during secondary processing such as bending and cutting. To avoid secondary processing, origami technology is proposed, and two types of honeycomb sandwich structures are designed and produced. The deformation behaviors and mechanical properties of honeycomb structures were investigated by the three-point bending test and flatwise compressive test. The load-displacement curve obtained at the room temperature indicates that the deformation process can be approximately categorized into three zones, namely linear-elastic zone, plastic-plateau zone and densification zone. The experimental results show that the bending stiffness and compressive strength of the honeycomb structures are approximately 0. 32 k N·m2 and 0. 39 MPa, respectively; the honeycomb structure manufactured based on origami technology has good mechanical properties.

 

　　1 蜂巢夹层结构

 

　　21世纪, 在汽车、船舶以及航空航天领域中, 具有高强度、高刚度和轻量化的结构材料是不可或缺的[1,2]。其中的蜂巢夹层结构受到越来越多研究者的青睐。最早应用在飞机上的蜂巢夹层结构是在第二次世界大战期间, 它是由校花木单片制成。此后, 陆续出现了金属、玻璃钢、合金等材料的蜂巢夹层结构。这种结构材料不仅具有良好的力学性能, 而且还具有良好的抗冲击性、可设计性、隔音性、吸音性、耐热性等等[3,4,5,6]。

 

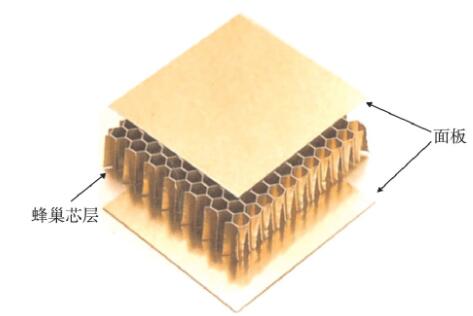
　　蜂巢夹层结构实际上是由蜂窝芯层和2个薄面板组成的[7,8,9], 如图1所示。

 

　

 

　　图1 蜂巢夹层结构示意图  

 

　　许多研究结果表明, 面板主要承受拉伸和压缩载荷, 芯层承受横向剪切载荷, 并使面板保有较高的特定弯曲刚度[4,6,8,9,10]。并且, 蜂巢芯层通过其失效机制影响夹层结构的面外压缩行为和能量吸收能力。为了更好地提高蜂巢结构的刚度和强度, 近年研究者更热衷于重新检查和优化蜂巢单元细胞以及几何形状。穆罕默德的研究小组讨论了六边形蜂巢的不同角度 (即60°、90°、120°) 对结构强度的影响, 发现120°的正六边形具有更高的强度[11]。此外, 也有研究小组通过使用不同的材料, 如金属箔, 塑料箔, 由碳纤维、玻璃纤维制成的复合材料来制造具有不同单元细胞形状 (例如三角形、正方形、五边形、六边形和八边形) 的蜂巢结构[2,12]。

 

　　目前为止, 大多数蜂巢结构都是由传统技术制造的。该技术主要是运用扩展方法来实现蜂巢结构, 如图2所示;但是, 这种技术在蜂巢的壁与壁之间必须要用粘接或焊接的方法进行固定[13], 这将需要其他大型设备来完成, 无形中增加了工时和成本, 而且对于断面不规则的结构 (如机翼和发电机叶片) 来说, 二次加工是不可避免的。这对于较薄的金属箔或其他片状材料来说, 在二次加工中蜂巢壁容易塌陷, 并且加工装置非常昂贵。减少或避免二次加工是一个关键问题。目前, 折纸技术吸引了大批材料设计者和建筑设计者的关注[14]。它起源于日本传统的折纸艺术[5]。这种技术可以根据空间几何学设计出形状复杂的蜂巢芯层, 并直接把平面图形变成三维立体结构[15], 无须进行二次加工。该方法的优点是可以根据波形和开口位置的变化设计出任意高度的蜂巢芯层, 在短时间内以低成本制造出符合市场需求的蜂巢结构。Saito小组在这一领域做了大量工作, 并基于折纸技术成功地设计了复杂的蜂巢结构[14,15]。

 

　　

　　图2 扩展方法的示意图[13]   

 

　　在本研究中, 基于折纸技术原理, 设计了正六角形蜂巢结构 (角度为120°) , 并在蜂巢的壁与壁之间设计了爪来固定, 无须使用黏接剂, 如图3所示, 并且利用一种新的制造方法 (即折叠和弯曲的工艺) 制作了2种类型的铝制蜂巢结构试样:一种是使用普通黏合剂固定的试样 (传统的固定方式) , 另一种是使用铝爪固定的试样 (专利2015-114459, 日本) [16,17]。通过弯曲实验及压缩实验, 比较了这2种固定方式对该结构力学性能的影响。结果表明, 采用铝爪固定的方式是可行的, 并且该结构具有优异的力学性能。本研究提供了一种用于制造高强度轻质的蜂巢结构的新方法, 并有望广泛应用于交通运输和航空航天等领域。

 

　

　　图3 基于折纸技术的蜂巢结构爪子示意图   

 

　　2 试样制作与实验

 

　　根据折纸技术的原理, 采用Auto CAD软件设计了蜂巢芯层的展开图。蜂巢的单元细胞形状为正六边形, 单元尺寸是19 mm, 芯层高度是25 mm。将设计的尺寸数据导入电脑, 直接在纸或者其他片状材料上切割出折痕及开口线。

 

　　本研究中, 蜂巢芯层和面板都由铝箔制成, 该铝箔购自UACJ铝箔公司 (东京, 日本) , 其密度为2.7g/cm3。图4展示的是蜂巢夹层结构的制造原理图。首先利用Auto CAD设计展开图, 然后将尺寸导入电脑, 利用切割装置直接在铝箔上切割出折痕和开口线, 接着采用折叠弯曲工艺制作出不同断面形状的蜂巢芯层, 最后粘贴上面板。本研究中的蜂巢芯层的铝箔厚度为0.1 mm, 面板的铝箔厚度为0.8mm, 芯层高度为25 mm。为了考察固定方式是否会对蜂巢结构的力学性能造成影响, 制作了2种类型的试样:一种是由普通的黏接剂 (Cemedine公司, 东京, 日本) 粘接而成;另一种是自行设计的铝爪固定。

 

　

 

　　图4 蜂巢夹层结构的制造原理图   

 

　　针对2种类型的试样, 进行了弯曲和平面压缩实验。2种试样的尺寸一样, 图5所示的是由铝爪固定的试样。图5 (a) 是用来做弯曲实验的试样, 图5 (b) 是用来进行压缩实验的试样。首先, 采用ASTM C393—2000实验标准, 使用万能实验机 (AG-50KNG, 岛津公司, 京都, 日本) 对2种试样进行三点弯曲实验。实验速度设定为2 mm/min, 支撑杆的跨度为250 mm。为了确保实验的准确性, 每种样条至少测试3次。通过式 (1) 和 (2) 分别计算蜂巢夹层结构试样的理论弯曲刚度 (DS) 和实际弯曲刚度 (D) , 并用式 (3) 计算其刚度系数 (CD*) 。

 

　　式中:DS是面板的弯曲刚度;E是铝的弹性模量;b1是试样的宽度;t1是面板的厚度;H是面板与芯层之间的距离。

 

　　式中:D是蜂巢结构的弯曲刚度;P是弯曲时承受的最大载荷;δ是蜂巢结构的变形量;l是支撑梁跨度。

 

　　根据ASTM C365—2000实验标准, 使用同样的试验机 (AG-50KNG, 岛津公司, 京都, 日本) 对蜂巢芯层进行了平面压缩试验。所有测试均使用50 kN的测力传感器和0.5 mm/min的压缩速度进行。每种试样都测量了3次以上。根据实验得到的荷载-位移关系曲线, 由式 (4) 计算了蜂巢芯层的实际抗压强度 (σ) 。此外, 蜂巢芯层的理论抗压强度 (σc) 由式 (5) 进行计算。

 

　　式中:P是压缩时承受的最大载荷;A是芯层横断面的面积。

 

　　式中:σy是铝的屈服强度;υ是铝的泊松比;t是芯层壁的厚度;b是单元细胞的尺寸。

 

　　

 

　　图5 铝爪固定的试样  

 

　　3 结果与讨论

 

　　图6展示了一个蜂巢夹层结构试样在三点弯曲试验中受到集中载荷而出现局部屈曲现象的典型例子。明显看出, 无论是哪种类型的试样, 在受到试验机压头挤压后, 面板的中部都出现了大变形, 并且蜂巢芯层都有坍塌的现象。值得特别注意的是, 由铝爪固定试样的蜂巢壁与壁之间有裂开现象, 如图6 (b) 所示, 猜测这将会对蜂巢结构的抗弯性能造成一定的影响。

 

　

 

　　图6 蜂巢夹层结构坍塌图   

 

　　此外, 通过三点弯曲实验还获得了蜂巢夹层结构的典型的载荷-位移关系曲线, 如图7所示。图中, 实线表示由普通黏合剂固定的试样, 虚线表示由铝爪固定的试样。这2条曲线都显示了蜂巢结构的变形特征, 分为线弹性区域、塑性平台区域和致密化区域3个。这与Ansari的报告类似[9]。在初始区, 蜂巢夹层结构发生弹性弯曲变形, 因此载荷呈线性增加。当载荷达到临界值时, 芯层开始变形, 细胞壁开始起皱, 如图6所示, 因此载荷迅速下降, 进入第2变形区域。这是因为这种结构的塑性铰在蜂巢壁塌陷时发生。随后进入第3变形区域, 局部的压缩变形将变成蜂巢壁材料本身的压缩变形而持续下去, 铝箔随着连续压缩而变得致密化, 因此载荷变成了一条平缓的线。在三点弯曲实验中, 蜂巢夹层结构除了会发生弯曲变形以外, 还会发生剪切变形。对于这一点, 我们在今后的研究中会进行具体的调查。

 

　

　　图7 蜂窝结构的弯曲行为   

 

　　同时, 无论哪种试样, 它们的最大载荷均大于0.8 k N, 并且试样被压缩约30 mm后, 样品的负载均保持在0.3 kN左右。对比2种试样, 由铝爪固定的试样的最大载荷 (0.84 kN) 略低于由黏接剂粘接的试样的最大载荷 (0.91 kN) 。这可能是因为由铝爪固定的试样在集中载荷压缩的过程中壁与壁之间发生了分离, 如图6 (b) 所示, 因而减弱了蜂巢结构的最大载荷;但是由于最大载荷仅降低了8%左右, 因此对于应用来说不会有太大的影响。另外, 根据式 (1) 计算出弯曲试样的理论弯曲刚度值约为1.12kN·m2。根据图7的实验结果, 由式 (2) 算出2种试样的实际抗弯刚度 (D) 均为0.32 kN·m2。这很可能是由于在弯曲实验过程中, 面板与芯层之间黏胶处出现了微小裂纹, 甚至有可能发生了局部塌陷, 从而导致实验值低于理论值。基于实际刚度和理论刚度, 利用式 (3) 计算出试样的刚度系数为0.29。

 

　　图8展示的是压缩试验后蜂巢芯层的外观照片。由图可知, 在10 mm的压缩后, 无论试样的固定方式如何, 蜂巢结构都已经完全变形, 蜂巢壁已经塌陷。此外, 2种试样存在明显的差异。在压缩过程中, 由铝爪固定的试样, 图8 (a) 所示, 蜂巢的相邻壁之间在压缩过程中横向裂开;由黏合剂固定的试样, 黏合的部分并没裂开, 是整体坍塌。这是因为由铝爪固定的试样, 其蜂巢壁仅在爪的位置固定, 当施加垂直载荷时, 细胞壁的其他位置是可自由移动的, 黏接剂固定的蜂巢壁被黏合剂完全粘合, 在压缩载荷下不容易脱胶, 因而整体坍塌。需要注意, 图8 (a) 中铝爪固定的位置在压缩过程中并没有裂开, 还处于固定状态, 因此不会对蜂巢结构的强度产生很大的影响。

 

　

　　图8 压缩试验后蜂巢芯层的外观图   

　　图9是蜂巢结构在平面压缩实验中所获得的载荷-位移关系特征曲线图。很明显, 2条曲线都表示蜂巢芯层在压缩过程中的变形分为线弹性区域、塑性平台区域和致密化区域3个, 这与蜂巢夹层结构在三点弯曲试验中的载荷-位移关系曲线相似。从图可以看出:试样被压缩约10 mm后, 由黏接剂固定的试样 (实线) , 最大载荷约为5.1 kN;由铝爪固定的试样 (虚线) , 最大载荷约为4.95 k N, 比由黏接剂固定的试样略降低了2.9%左右。基于图9实验结果, 由式 (4) 计算得到, 无论是由黏接剂固定还是由铝爪固定的试样, 其实际抗压强度都约为0.39MPa。这表明固定方式并不会对蜂巢结构的抗压性能造成影响。然而, 由式 (5) 计算出的蜂巢芯层的理论强度约为0.98 MPa, 高于实验值。这主要是由于在进行平面压缩实验时, 只对蜂巢芯层进行了测试, 而未在测试时粘贴面板 (面板会增强蜂巢结构的抗压性能) , 导致蜂巢芯层在压缩过程中直接受压, 极易发生局部塌陷, 所以实验值低于理论值。

 

　

 

　　图9 蜂巢芯层的压缩行为   

 

　　4 结论

 

　　在本研究中, 基于折纸技术提出并设计了正六角形蜂巢结构 (角度为120°) , 并且通过新的制造方法 (即折叠和弯曲的工艺) 制造了具有高强度轻质的铝制蜂巢结构。通过三点弯曲试验和平面压缩试验, 对比了黏合剂固定的试样与铝爪固定的试样的破坏方式, 发现铝爪固定的试样在局部载荷和均匀载荷下壁与壁之间容易裂开, 但是在铝爪固定的位置不会被破坏, 因此不会造成大的影响。此外, 在三点弯曲试验和平面压缩试验过程中, 2种试样的变形都呈现出典型的荷载-位移关系曲线特征, 即分为线弹性、塑性平台和致密化3个变形区域。实验结果表明, 这2种类型的试样的弯曲刚度均为0.32kN·m2, 抗压强度均为0.39 MPa, 这说明铝爪固定方式不会影响蜂巢结构的力学性能。综上所述, 利用折纸技术设计蜂巢结构不仅避免了二次加工, 而且该结构也具有良好的力学性能, 有望在船舶和航空航天领域得到实际应用。

 

　　参考文献

 

　　[1]ASPRONE D, AURICCHIO F, MENNA C, et al.Statistical finite element analysis of the buckling behavior of honeycomb structures[J].Composite Structures, 2013, 105:240-255.

　　[2] VINCENZO Crupi, EMRE Kara, GABRIELLA Epasto, et al.Theoretical and experimental analysis for the impact response of glass fiber reinforced aluminium honeycomb sandwiches[J].Journal of Sandwich Structures and Materials, 2016, 20:1-28.

　　[3] KUNIMOTO, T.The aluminum alloy sandwich construction[J].Journal of Japan Institute of Light Metals, 1990, 40 (5) :390.

　　[4]SEBASTIAN Fischer.Aluminium fold cores for sandwich structure application:Mechanical properties and FE-simulation[J].ThinWalled Structures, 2015, 90:31.

　　[5] HARBIN R.Secrets of origami:the japanese art of paper folding[M].[S.l.]:Dover Publications Inc, 1997.

　　[6]MILLER W, SMITH C W, EVANS K E.Honeycomb cores with enhanced buckling strength[J].Composite Structures, 2011, 93 (3) :1072-1077.

　　[7] RAYJADE G R, SESHAGIRI Rao G V R.Study of composite sandwich structure and bending characteristics:a review[J].International Journal of Current Engineering and Technology, 2015, 5 (2) :797.

　　[8] KAMAN M O, SOLMUZ M Y, Turan K.Experimental and numerical analysis of critical buckling load of honeycomb sandwich panels[J].Journal of Composite Materials, 2010, 44 (24) :2819-2831.

　　[9] ZAHID Ansari Mohd, JANGIR Jitendra, VERMA Lokesh, et al.Compressive behaviour of polymer/honeycomb sandwich composites[J].American Journal of Materials Science, 2015, 5 (3C) :4.

　　[10] WAHL L, MAAS S, WALDMANN D, et al.Shear stresses in honeycomb sandwich plates:analytical solution, finite element method and experimental verification[J].Journal of Sandwich Structures and Materials, 2012, 14 (4) :449-468.

　　[11] MOHAMMED D F, AMEEN H A, MASHLOOSH K M.Experimental and numerical analysis of AA3003 honeycomb sandwich panel with different configurations[J].Am J Sci Ind Res, 2015, 6 (2) :25.

　　[12]FOTSING E R, LECLERC C, SOLA M, et al.Mechanical properties of composite sandwich structures with core or face sheet discontinuities[J].Composites Part B, 2016, 88:229-239.

　　[13] WANG Lijun, SAITO Kazuya, GOTOU You, et al.Design and fabrication of aluminum honeycomb structures based on origami technology[J].Journal of Sandwich Structures and Materials, 2017:109963621771464.

　　[14] SAITO K, PELLEGRINO S, NOJIMA T.Manufacture of arbitrary cross-section composite honeycomb cores based on origami techniques[J].Journal of Mechanical Design, 2014, 136 (5) :1-9.

　　[15] SAITO K, NOJIMA T.Development of light-weight rigid core panels[J].Journal of Solid Mechanics and Materials Engineering, 2007, 1 (9) :1097-1104.

　　[16] SAITO K.Manufacture apparatus and method of honeycomb core:Japan, 2014-087816[P].2014.

　　[17] GOTOU Y, SAITO K.Honeycomb cores and their fabrication method:Japan, 2015-114459[P].2015.