自平衡独轮滑板车的动力学原理探析

　　摘    要：　本文讨论自平衡独轮滑板车的动力学原理。将滑板车简化为由带骑手的车架和车轮组成的双刚体系统。基于动量矩定理列写车轮纯滚动条件下的动力学方程。对滑板车加速减速和转弯的动力学过程，以及骑手的直立稳定性给出理论解释。导出由控制系统保证的滑板车自平衡过程的稳定性条件。

　　关键词 :     自平衡滑板车;独轮滑板车;陀螺力矩;运动稳定性;

　　Abstract：　The dynamics of a self-balancing one-wheel scooter is analyzed in this paper. The one-wheel scooter is simplified as a two-body system composed of a frame with rider and a wheel. Under the nonholonomic constraint conditions of pure rolling of the wheel, the dynamic equations of the system are derived by use of the theorem of angular momentum. The acceleration and deceleration, the turning motion of the scooter, and the standing stability of the rider are examined theoretically. The stability criteria of self-balancing procedure by control system are derived.

　　Keyword：　self-balancing scooter; one-wheel scooter; gyroscopic torque; stability theory of motion;

　　自2008年北京奥运会上自平衡的赛格威车首次亮相以来[1],2015年出现了赛格威车缩小版的自平衡双轮滑板车[2]。与此同时，又有构造更简单的称为“Onewheel”的自平衡独轮滑板车问世(图1)[3]。这种新型的代步工具只有一个轮子，仅依靠驾车人的身体动作就能实现加速、减速和转弯等各种功能。虽然操纵难度比双轮滑板车更大，需要掌握更多技巧才能熟练驾驶，但骑手能感受到自由飞翔般地飘浮感觉，因而备受年轻人的青睐。各种新设计和产品不断涌现，促使自平衡滑板车的技术和产业在国内快速发展。

　　图1 自平衡独轮滑板车和骑手

　　自平衡滑板车的出现为力学科普提供了一个有趣的课题。重心高高在上的骑手如同一只倒置的复摆，稳定的自平衡是如何实现的？根据经典力学的基本原理，任何系统的运动状态只能依靠外力的作用改变。自平衡滑板车仅靠驾车人扭动身体就能改变运动状态应如何解释？独轮车与地面只有一个点接触，约束力不能形成绕垂直轴的力矩，转弯的动力从何而来？就上述问题本文讨论自平衡独轮滑板车的动力学原理。忽略骑手肢体动作引起的质量变化，将车架加骑手视为刚体，与车轮组成双刚体系统。设车轮相对地面做纯滚动，滑板车的运动被归结为非完整约束条件下双刚体系统的动力学问题。

　　自平衡独轮滑板车的构造十分简单。在钢制框架的中心用轴承安装一只粗壮的橡胶轮，前后各装有一片木踏板(图2)。骑手跨立在车轮前后两侧，通过重心移动改变足底对前板或后板的压力。板内安装的加速度计将测出的信息通过控制系统传输至驱动电机，以控制车轮的加速或减速。

　　图2 自平衡独轮滑板车

　　需要转弯时，与驾驭滑雪板或冲浪板的方法类似，驾车人带动车体向要转弯的一侧倾斜。利用与自行车类似的“离心力效应”和“陀螺效应”，倾斜车体的重力与支承力构成力偶，使旋转中的车轮进动，出现绕垂直轴的转动。由此产生的陀螺力矩与重力矩平衡[4]。车体绕垂直轴的转动使直线轨道发生偏转，从而实现转弯动作。沿曲线轨道行进的车体和人体产生离心惯性力，使驾车人恢复直立姿态避免摔倒。独轮滑板车厚重车轮的动量矩明显大于自行车的前轮，陀螺效应也更为明显。

　　将车架和固定在车架上的骑手作为刚体B0，车轮作为刚体B1。独轮滑板车是由B0和B1以圆柱铰连接组成的双刚体系统{B}(图3)，其中，R为车轮半径，B1与地面的接触点记为P。将车轮不转时{B}固结成的刚体记作B*。以B*的质心Oc为原点，建立平动参考坐标系(Oc-XY Z),X和Y轴与地面平行，Z轴为垂直轴。设(Oc-XY Z)绕垂直轴转过φ角的位置为(Oc-x0y0z0),x0轴为车轮的前进方向。继续绕x0轴转过ψ角为(Oc-x1y1z1),y1轴为车轮的旋转轴。最终(Oc-x1y1z1)绕y1轴转过θ角为刚体B*的主轴坐标系(Oc-xyz),z轴沿骑手身体的纵轴(图4)。

　　图3 双刚体系统

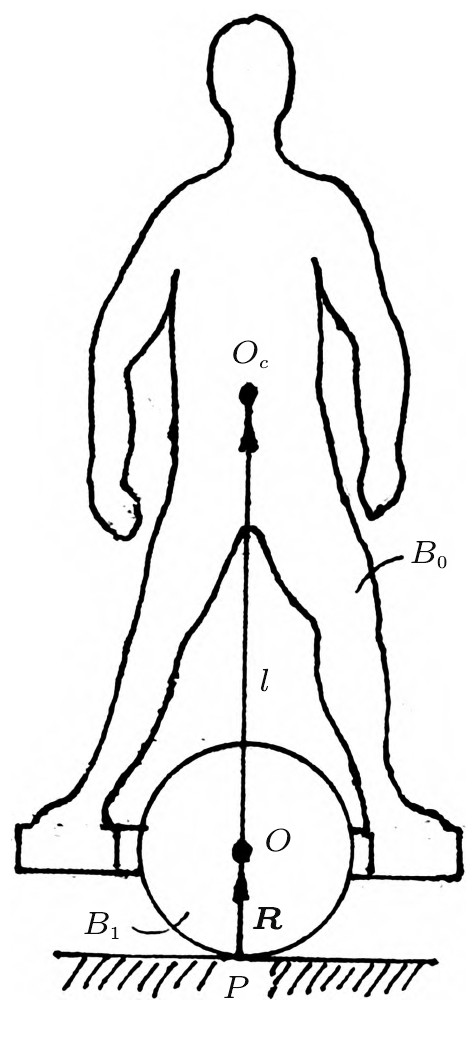
　　图4 参考坐标系

　　以骑手在车板上直立，滑板车匀速直线前行作为稳态运动。即φ=θ=ψ=0，?=?0，质心速度vcx=R?0,vcy=0。其中?为转速，?0为稳态转速。骑手利用身体向前或向后的倾斜动作控制车速。当骑手向前倾斜时，因重力对前板的压力大于后板，使车板产生角加速度。安装在车板内的加速度计将测出的信息输入控制系统，积分后转换为转角θ和角速度信息，控制驱动力矩使车轮加速。如向后倾斜则控制力矩方向相反，车轮减速。即使在稳态行进过程中，若骑手因扰动向前倾斜，车体会自动加速，产生向后的惯性力使骑手恢复原位。向后倾斜则减速产生向前的惯性力。因此这种速度控制系统也是骑手站立稳定性的根本保证。

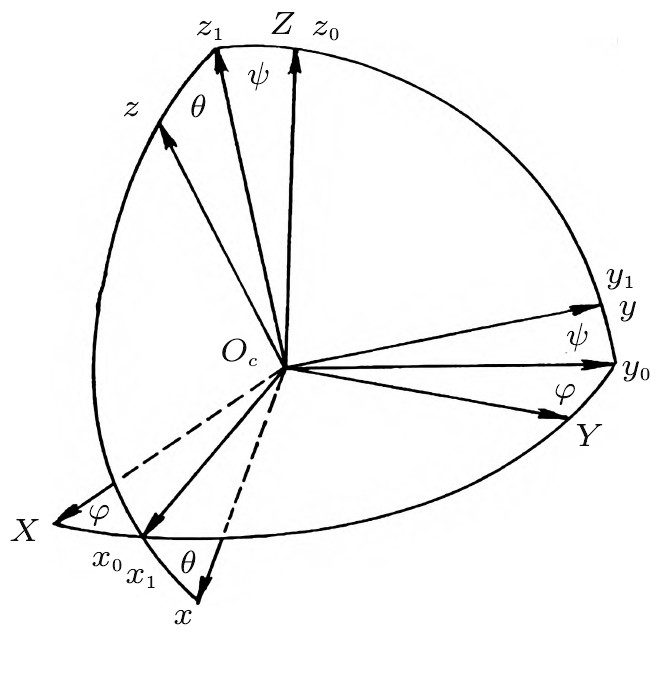
　　仅保留小量φ，θ，ψ及其导数的一次项，设i,j,k为x,y,z各轴的基矢量，B*的角速度为ω=˙ψi+˙θj+˙φk。设B1相对B*的旋转速度为?=?j，从B1的质心即轮心O至B*的质心Oc引矢径l=lk，从B1与地面的接触点P至轮心O引矢径R=Rk (图3)。设Oc的速度为vc=vcxi+vcyj+vczk，则P点的速度为vP=vc+(R+l)×ω+R×?，导出

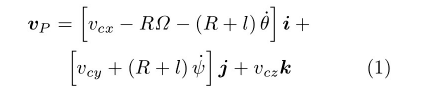
　　设车轮B1在地面上作无滑动的纯滚动，令vP=0，引出非完整约束条件

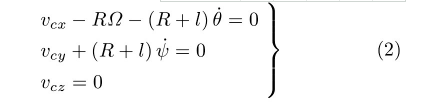
　　利用此约束条件确定质心速度vc，即

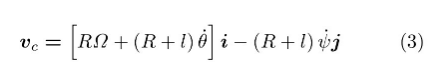
　　将参考坐标系的原点Oc移至轮心O，设{B}的质量为m，以(O-xyz)为参考坐标系，列写{B}在重力mg和约束力F作用下的质心运动方程

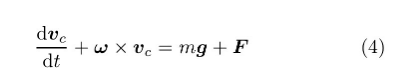
　　其中波浪号表示动坐标系(O-xyz)中的局部导数。将式(3)代入，解出约束力F，即

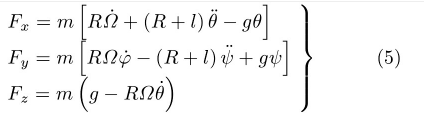
　　设车轮B1的质量为m1，对O点的极惯量矩为J0，动量矩为，省略号为含的小量。外力矩为电机驱动力矩Mc=Mcj和约束力F对O点的主矩F×R。以(O-xyz)为参考坐标系，列写B1对质心O的动量矩定理

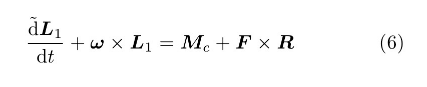
　　将其中的F以式(5)代入，令J=J0+m R2，导出矢量方程(6)在Oy轴上的投影式

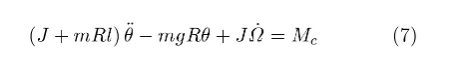
　　为讨论系统{B}的运动，设B*对(Oc-xyz)各轴的主惯量矩为A,B,C，则{B}对Oc点的动量矩为。列写{B}对质心Oc的动量矩定理时，控制力矩Mc是系统的内力矩而不再出现，重力mg因作用点与矩心重合也不出现，仅有的外力矩来自地面约束力F。以(Oc-xyz)为参考坐标系，列出

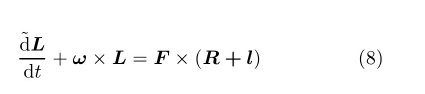
　　将式(8)中的F以式(5)代入，向(Oc-xyz)各轴投影，得到

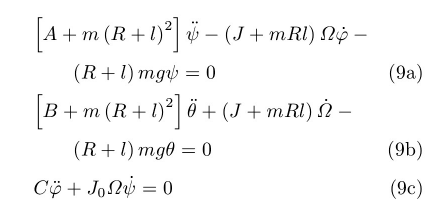
　　若不加控制，令式(9b)中，则成为倒置的复摆方程，θ=0为不稳定的直立状态。若施加控制，采用与θ成比例的最简单的控制方案

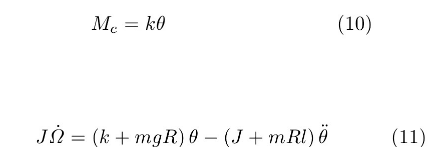
　　代入式(7)后解出

　　从式(9b)和式(11)消去，引入α=m Rl/J，得到

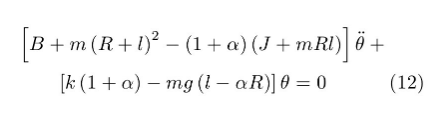
　　将车轮视为均质圆盘，令J0=m1R2/2，则J=m*R2,m*=m+(m1/2)，引入α=ml/(m*R)。将式(12)中的系数中带负号部分化作

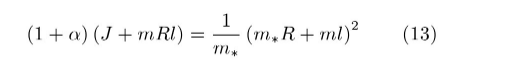
　　因m>>m1,m*与m接近，若将式(13)右项的分子和分母中的m*均以m近似代替，则化作m (R+l)2。可推知式(12)中的系数近似等于B。方程(12)的特征方程为

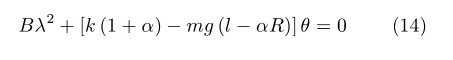
　　若令控制系数k满足

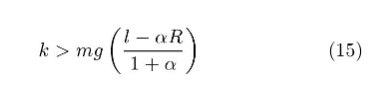
　　则特征根为纯虚数，θ=0为稳定平衡，证明骑手的直立状态对前后侧扰动保持稳定。但根据运动稳定性的一次近似理论，线性系统的特征根实部为零属于临界情形，只能判定线性系统的零解稳定，而不能判断未经线性化的原系统的稳定性[5]。

　　为提高控制过程的灵敏性和稳定性，可在简单控制规律(10)中增加随变化的因素，变为

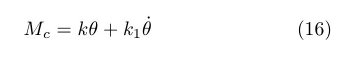
　　则方程(12)中应增加一项，特征方程变为

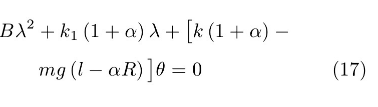
　　因特征根的实部均为负数，根据李雅普诺夫一次近似稳定性理论，此线性系统的零解变为渐近稳定，且能判定原系统的零解亦渐近稳定。

　　对滑板车变向和转弯的解释须利用方程(9a)和(9c)。设车轮转速在转弯过程中维持常值?0不变。当骑手开始向右侧倾斜时，尚未变向的车体仍维持短暂的。方程(9a)成为以ψ为变量的倒置复摆的动力学方程。重力导致的倾覆角加速度从零开始按指数规律增长。当增长至有角速度出现时，引起车轮的动量矩矢量L1进动，产生陀螺力矩。依据方程(9c)，车体出现绕z轴的角加速度，使前进方向发生改变趋势。所产生的惯性力矩与车轮的陀螺力矩平衡。当角加速度随时间积累到有φ角出现时，转弯过程完成，直线运动变为曲线运动。所产生的离心惯性力推动骑手恢复原位，保证了骑手在侧向平面内的站立稳定性。

　　为分析此稳定过程，令方程(9a)和(9c)中?=?0，将ψ和φ视为扰动量，导出此线性方程组的特征方程其中

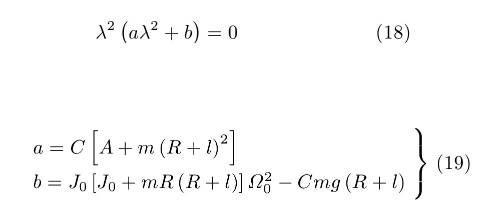
　　在方程(18)确定的特征值中，λ=0的零特征值体现了变量φ因无恢复力导致的随遇性。另两个特征值的纯虚根条件为b>0，即ψ和φ耦合运动的零解稳定性条件。从中导出车轮的最低转速

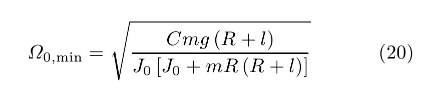
　　只要使车轮转速满足?0>?0,min，骑手对左右侧扰动的站立稳定性就能得到保证。

　　与前文对前后侧扰动的稳定性分析类似，线性系统的零解稳定不能判断原系统的稳定性。但实际上任何机械系统均难以避免阻尼因素，若在系统中增加与角速度˙ψ成比例的阻尼项，则线性系统的零解即转为渐近稳定。根据李雅普诺夫一次近似稳定性理论，未经线性化的原系统的零解亦渐近稳定。

　　以上对滑板车运动过程的分析表明，骑手的肢体动作或控制电机的驱动制动，最终均转化为重力和地面摩擦力对车体和骑手的作用。滑板车运动状态的改变是重力和地面摩擦力的作用结果。任何系统都不可能依靠内力改变运动状态。

　　参考文献

　　[1]刘延柱.动力滑板车漫话力学与实践,2009,31(6):95-96Liu Yanzhu.Talk on segway human transporter. Mechanics in Engineering. ,2009,31(6):95-96 (in Chinese)

　　[2]刘延柱缩小的赛格威车-谈自平衡滑板.力学与实践,2017.,39(2):208-210Liu Yanzhu.A miniature segway-talk on self-balancing scooter. Mechanics in Engineering,2017,39(2):208-210(in Chinese)

　　[3] Onewheel:独轮电动滑板让你纵横驰骋

　　[4]刘延柱关于自行车的稳定性力学与实践, 2012,34(2):90-93Liu Yanzhu.On the stability of bicycle Mechanics in Engineering ,2012 ,34(2):90-93 (in Chinese)

　　[5]刘延柱高等动力学第2版北京高等教育出版社,2016