
1. 引 言
雨贡纽( Hugoniot) 数据是材料从同一初始状态出发、经过不同的冲击压缩达到的终态的集合,描述了冲击波后任一压缩态下热力学状态量之间的内在联系. 一方面,通过 Hugoniot 数据的测量,能够研究材料在高压下的相变和物态方程; 另一方面,已知 Hugoniot 数据也是进行冲击波实验设计的基本材料参数.
Bi 在冲击波加 载 下 会 出 现 较 复 杂 的 相 变 序列,是进行冲击相变研究的典型材料; 而其低压区复杂的多形相变和反常熔化,使得该压力段内Hugoniot 数据的测量对研究材料弹塑性响应和冲击相变具有重要意义. 早期 Duff 等就利用基于电探针技术的自由面速度法测量了 Bi 的低压 Hugoniot数据,并在 2. 5 GPa 附近观测到了 BiⅠ( 斜方六面体结构)→BiⅡ( 底心单斜结构) 相变,相变压力较静压的结果偏高. 之后 Romain利用电探针技术测量了 Bi 在 20 GPa 压力下的 Hugoniot 数据,实验发现在 7 GPa 附近的冲击压缩下 Bi 发生了 BiⅢ( 四方晶系结构)→BiⅤ( 体心立方结构) 相变. 随后,国外相继利用多种加载手段对 Bi 的冲击相变热力学、动力学以及多相物态方程进行了研究. 但作为上述研究基础工作的 Bi 的低压区 Hugoniot 数据,却存在较大的分散性,由此导致获得的相边界的不确定度较大,对 Bi 低压段多相物态方程的建立存在较大的影响. 因而有必要对 Bi 在低压段的 Hugoniot数据进行精确测量.
目前人们还不能完全从理论的方法确定材料的 Hugoniot 数据,必须借助于实验测量. 而现有的Hugoniot 数据测量中,冲击波速度 D 主要利用电探针技术测量冲击波在已知厚度样品中的走时( 又称“渡越时间”) 得到. 由于飞片在加速过程中不可避免地会产生倾斜和弯曲变形,而样品内也存在复杂的波系作用,因此必须要对由此引起的冲击波走时进行修正,该修正量不确定度的引入,导致了冲击波速度合成不确定度的加大; 同时,电探针法作为一种接触式的测量方法,要求了电探针的有效触发和快时间响应,然而电探针的低压触发响应较慢,这使得材料低压区 Hugoniot 数据的精密测量变得更加困难.
本研究工作采用反向碰撞的实验技术,探索了通过样品 /窗口界面粒子速度剖面的测量获得材料低压区 Hugoniot 数据的可行性. 利用该方法,获得了 Bi 在 10—45 GPa 压 力 范 围 内 的 高 精 度Hugoniot 数据,并与已有的文献报道数据进行了比较.
2. 实验方法
对于静止靶初始状态为常压的情形,由平面冲击波阵面前后状态满足质量、动量与能量守恒关系得到 Rankine-Hugoniot公式【1-3】
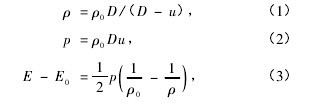
式中 ρ,D,u,p 和 E 分别表示冲击波阵面后的密度、冲击波速度、粒子速度、压力和比内能,下标 0 表示初始状态.目前还没有直接测量比内能 E 的方法,而压力p 及密度 ρ 测量的精度较低,因此,Hugoniot 数据测量实验通常是对冲击波速度 D 和粒子速度 u 进行测量. 对于大多数凝聚介质,D-u 曲线在一定范围内满足下列线性关系:【4】
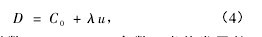
式中 C0和 λ 为常数,即 Hugoniot 参数. 当前发展的实验方法主要有绝对测量法和对比测量法. 在上述两种方法中,冲击波速度 D 都是通过测量冲击波在一定厚度样品中的走时得到,其精度主要取决于冲击波走时的精度. 为提高冲击波走时的测量精度,需要控制入射冲击波的变形程度( 弯曲和倾斜等) ,并在样品前后界面设计合理的探针布局,通过一定的统计分析模型对冲击波走时进行修正. 在绝对测量法中,由于飞片和样品为同种材料,而且初始状态也完全相同,冲击波后粒子速度 u 通过测量飞片速度 W 得到( u = W /2) ; 在对比测量法中,冲击波后粒子速度 u 无法直接测量得到,必须通过相关量的间接测量,利用阻抗匹配法获得. 由于飞片和样品材料阻抗不匹配,粒子速度的不确定度还需考虑飞片材料 Hugoniot 镜像线近似二次冲击绝热线或卸载线而引入的不确定度.本研究采用反向碰撞法测量 Hugoniot 数据,其原理如图 1. 如图 1( a) 的 X-t 图所示,在拉格朗日坐标系中,当作为飞片的样品以速度 W 撞击静止的透明窗口时,将分别在样品和窗口中产生左、右行冲击波,并相应地使样品和窗口中的压力、粒子速度等状态由初始的 p0s,u0s,p0w,u0w突变为 ps,us,pw,uw.在欧拉坐标系中,根据界面连续性条件可以得到【5-6】
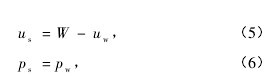
根据( 2) ,( 5) 式,窗口和样品中的冲击压力可表示为【7-8】
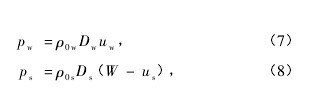
式中 Ds和 Dw分别为样品和窗口内的冲击波速度.根据图 1( b) 的 p-u 关系,由( 6) —( 8) 式得到样品内的冲击波速度 Ds为【9】
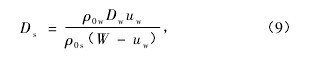
式中 ρ0s和 ρ0w分别为样品和窗口的初始密度. 如果窗口材料的 D-u 曲线满足线性关系【10】
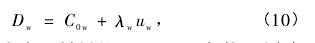
式中 C0w和 λw为窗口材料的 Hugoniot 参数,则( 9)式可表示为【11】
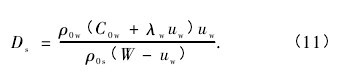
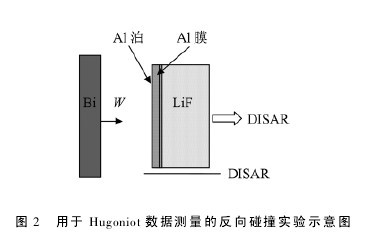
由 ( 5 ) ,( 11 ) 式 可 见,在 反 向 碰 撞 法 测 量Hugoniot 数据的实验中,只需要测得飞片 ( 样品) 击靶速度 W 和窗口的波后粒子速度 uw,就可获得样品的粒子速度 us( = W - uw) 和对应的冲击波速度 Ds.实验在中国工程物理研究院流体物理研究所的火炮和二级轻气炮上进行,实验中使用的 Bi 样品纯度为 99. 84% ,密度为 9. 808 g/cm3,样品加工成35 mm × 2 mm( 用于火炮发射实验 ) 和 27 mm ×1. 7 mm( 用于二级轻气炮发射实验) 的圆片,两端面作光学抛光. 装置示意图如图 2 所示,将圆片状 Bi样品作为飞片安装在弹丸上,利用 37 mm 口径火炮( 获得较低的弹速和冲击加载压力) 和 28 mm口径二级轻气炮( 获得较高的弹速和冲击加载压力) 将弹丸发射至稳定的终点弹道速度 W,并撞击LiF 单晶窗口 . 飞片击靶速度 W 采用全光纤激光干涉测试技术( DISAR) 或磁测速系统测量,界面粒子速度剖面采用单点 DISAR 测量,该技术不存在干涉条纹丢失的问题. 为了提高测试界面对 DISAR 系统入射光的反射效率,窗口击靶面镀有 1 μm 的铝膜; 此外,为了避免真空靶室残留气体对测试的干扰,窗口击靶面贴有 8 μm 厚铝箔挡光层.【图2】
3. 实验结果及讨论
本研究共进行了 5 发实验,测量了 Bi 在 10—45GPa 压力范围内的飞片速度和样品 / 窗口界面粒子速度. 图 3 给出了在窗口中轴线上的单点 DISAR 系统所获得的界面粒子速度( 注: 图中没有给出速度剖面的卸载部分) ,从图中可以看出,在反向碰撞法中,Bi 样品直接与 LiF 窗口撞击,界面速度信号的上升前沿陡峭,紧接着是一个很平坦的平台,信噪比高,该平台速度即为窗口的冲击波后粒子速度 uw.【图3】
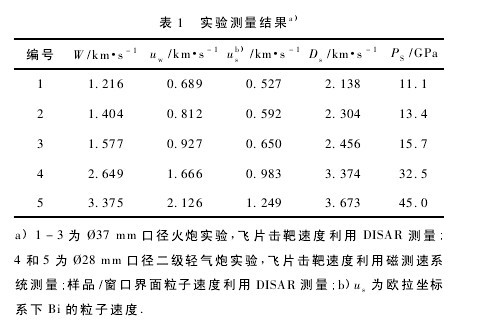
根据实验测量的飞片速度 W 和窗口处的粒子速度 uw,应用( 11) 式计算得到 Bi 的冲击波速度,实验结果见表 1,表中 PS为样品 / 窗口界面处的压力.【12】【表1】

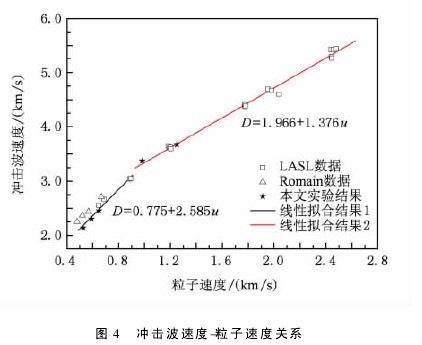
利用反向碰撞法得到的 Bi 样品的 D-u 关系如图4 所示,同时示于图中的还包括 Romain和 LASL的数据. 从图 4 中可以看出,在较高压力段本实验获得的数据同国外发表的数据较符合,低压段得到的实验数据具有很好的线性相关性,与 LASL 数据基本符合,但与 Romain 的数据相比略低. Romain 的数据采用电探针技术获得,而在低压下电探针触发响应可能受到弹塑性和多波结构的影响,触发一致性差. 由图4 可以看出,D-u 曲线可以分成两段: 在低压段,D-u曲线中冲击波速度 D 随着粒子速度 u 的增大而增大,呈线性相关,且斜率较大,在高压段,D-u 曲线中冲击波速度 D 也随着粒子速度 u 的增大而增大,也呈线性相关,但是斜率较小. 此 D-u 曲线拐折出现在粒子速度 0. 9 km/s 附近,对应的压力点约为 27 GPa,由实验获得的 Hugoniot 数据,结合 LASL 的数据,拟合得到【13】

经历了从 20 GPa 的初始熔化到 30 GPa 的完全熔化的压力区间,具体的压力区间有待进一步的声速和温度测量进行确定.【图4】
在测量 Bi 的 Hugoniot 数据实验中,不确定度主要来源于飞片速度 W、窗口界面粒子速度 uw以及窗口材料 Hugoniot 参数 C0w和 λ. 对于飞片速度 W,DISAR 测速的标准不确定度为 0. 1% ,磁测速的标准不确定度为 0. 25% ; 对于窗口界面速度 uw,其不确定度还包括窗口的折射率修正. 如果窗口材料Hugoniot 参数的不确定度按 0. 5% 计算,则根据不确定度传递规律,采用反向碰撞法获得的样品粒子速度标准合成不确定度不超过 1% ,冲击波速度的标准不确定度不超过 2% .由以上所述可知,本研究采用的利用 DISAR 获得 Bi 样品 Hugoniot 数据的实验方法可行,在低压区Hugoniot 数据测量不确定度优于电探针技术; 同时,该方法不涉及冲击波波形修正和冲击波走时的精确测量问题.
4. 结 论
通过在火炮和二级炮上进行的反向碰撞实验,得到了 Bi 在 10—45 GPa 冲击作用下 Hugoniot 数据. 实验结果表明:
1. 采用反向碰撞技术,测量 Bi 样品 / LiF 窗口界面的粒子速度和飞片速度,由界面连续性条件和Rankin-Rankine 关系获得样品中的冲击波速度,进而获得样品在低压段的 Hugoniot 数据,样品粒子速度 us的标准不确定度不超过 1% ,冲击波速度 D 的标准不确定度不超过 2% ,该方法同样适用于其他材料的低压 Hugoniot 数据测量;
2. 在 10—45 GPa 压力范围内,实验结果清楚地表明了 Bi 的 D-u 曲线存在明显的间断( 分为两段) ,并分别呈线性关系,其低压段和高压段的 D-u关系 可 分 别 表 述 为 D = 0. 775 + 2. 585 u 及 D =1. 966 + 1. 376 u,该拐折可能对应于 Bi 的冲击熔化,由此推断 Bi 在 27 GPa 附近发生了冲击相变( 固—液相变) ,具体的相变压力区间需要下一步进行的高压声速和温度的数据确定.