摘 要: 动静压轴承广泛应用于超高速切削电主轴,其工作性能对电主轴的可靠性及加工精度具有直接影响。传统动静压轴承设计以满足设计要求为原则,无法确保轴承的最优使用性能。为此以深浅腔体液动静压轴承为对象,对轴承结构的多目标优化设计进行研究。以轴承温升最小、油膜刚度及承载能力最大为目标函数,以浅腔深度、初始油膜厚度、进油孔径为设计变量,将参数取值范围作为限制条件,依托遗传算法,对动静压轴承开展优化设计,探寻最优方案。在对优化前后进行比较分析后发现,与优化前相比,动静压轴承油液温升、油膜刚度及承载能力在优化后均得到了改善,说明本次优化设计具有可行性。
关键词 : 动静压轴承;温升;油膜刚度;优化设计;遗传算法;
Abstract: Hydro-dynamic-static bearing is widely used in the ultra-high-speed machining of motorized spindle.Its working performance has direct impact on the reliability and machining accuracy of the motorized spindle.Traditional design of hydro-dynamic-static bearing is based on the principle of meeting the design requirements, which cannot ensure the optimal performance of the bearing.For this reason, the multi-objective optimization design of the deep-shallow-cavity hydro-dynamic-static bearing is studied.Taking the minimum temperature rise, the maximum oil film stiffness and the maximum bearing capacity as the objective function, the shallow cavity depth, the initial oil film thickness and the oil inlet diameter as the design variables, and the parameter range as the limiting condition, the dynamic-static bearing is optimized based on genetic algorithm.The oil temperature rise, oil film stiffness and bearing capacity of the dynamic-static bearing have been improved after the optimization, which indicates that the optimization design is feasible.
Keyword: dynamic-static bearing; temperature rise; oil film stiffness; optimization design; genetic algorithm;
0、 引言
动静压轴承具有精度高、稳定性好、抗干扰能力强的特点,广泛应用于测量仪器及精密机床,其润滑方式分为油润滑、水润滑及气体润滑[1]。当前,相关研究者对气体动静压轴承进行了大量研究。王云飞研究了动混合润滑静压气体轴承的动态、稳态设计,为缝式、孔-腔式、孔式动静压轴承设计奠定了理论基础[2];郭胜安等通过数值计算法及CFD仿真法分别深入研究小孔节流深浅腔动静压轴承的承载性能,验证了数值计算及软件仿真的正确性[3];吴怀超等分别采用有限体积法、遗传算法、有限元法结合正交试验法,优化设计了动静压轴承,为获得最优轴承参数即轴承特性提供了理论指导[4]。
传统动静压轴承设计以满足设计要求为基本原则,无法确保轴承使用的最佳性能,为此文中以深浅腔液体动静压轴承为对象,对其多目标优化设计进行研究,获得轴承最佳使用性能。

1 、动静压轴承结构分析
文中以应用于超高速切削电主轴的深浅腔液体动静压轴承为研究对象[5],其结构见图1。
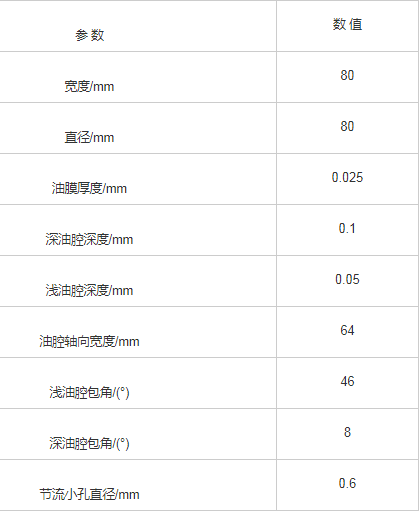
图1中,轴瓦上设置有4个由浅腔和深腔构成的阶梯型油腔,进油孔位于深腔中间部位。在液压力作用下,经节流器的高压油液从进油孔进入轴承油腔,润滑油在轴径高速转动下在轴承内部由深腔流入浅腔,填充整个腔体。深腔向浅腔流动过程中,油液流速降低,油膜压力增加,有效的降低了油腔内的湍流现象。出油口位于轴径与轴承之间的间隙,由于出油口间隙较小,油液流出阻力较大,致使轴承油腔可保持较大油膜压力。动静压轴承结构参数如表1所示。
图1 深浅腔动静压轴承结构图
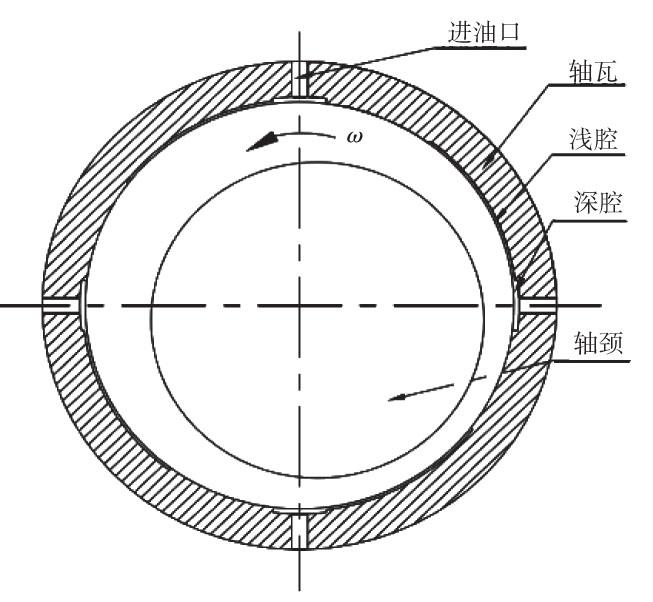
表1 动静压轴承结构参数
2 、多目标优化设计
2.1、 优化设计的数学模型
2.1.1、 目标函数
动静压轴承优化设计中,综合其整机结构要求及工况条件,选择目标函数。对于超高速电主轴系统,液体动静压轴承主要承载外部载荷[6],设计时将承载能力最大值作为优化设计目标函数。主轴转速越高,承载能力越大,但转速过大将致使加大轴承摩擦功耗,油温上升,油液粘度及油膜刚度下降,影响轴承工作性能[7]。因此设计中在考虑承载能力的基础上,还应综合考虑温升、油膜刚度及承载能力三者之间关系。文中以温升最小、刚度及承载能力最大三项指标作为优化设计的目标函数,即
2.1.2、 设计变量
动静压轴承在动压效应、静压效应共同作用下工作,动压腔为动压效应提供润滑油,而静压效应所需的润滑油则由专门静压供油系统所提供,润滑油经过油孔进入到轴承油腔,进油孔直径决定进油量,本文将进油孔直径作为设计变量[8]。初始油膜刚度作为油膜轴承的重要设计参数,对动静压轴承摩擦功耗、回转精度、刚度及承载能力具有直接影响,初始油膜厚度直接影响轴承使用寿命、工作性能及机床加工精度,所以,本次设计的优化变量为初始油膜厚度。静、动压腔结构是深浅腔动静压轴承的主要特点,动压效应和静压效应分别为浅腔和深腔,因此,二者均深受腔体深度的影响。由此在开展设计工作的过程中,把静压腔深度和动压腔深度分别设置为设计常量和设计变量。综上所述,文中将浅腔深度、初始油膜厚度、宽径比、进油孔直径作为优化设计中的设计变量,即
x=[dc h0 hp]T (2)
2.1.3、 约束条件
动静压轴承的优化设计的约束条件为
(a)进油孔径dc
0.6 mm≤dc≤0.7 mm
(b)初始油膜厚度h0
0.02 mm≤h0≤0.027 mm
(c)浅油腔深度hp
0.02 mm≤hp≤0.09 mm
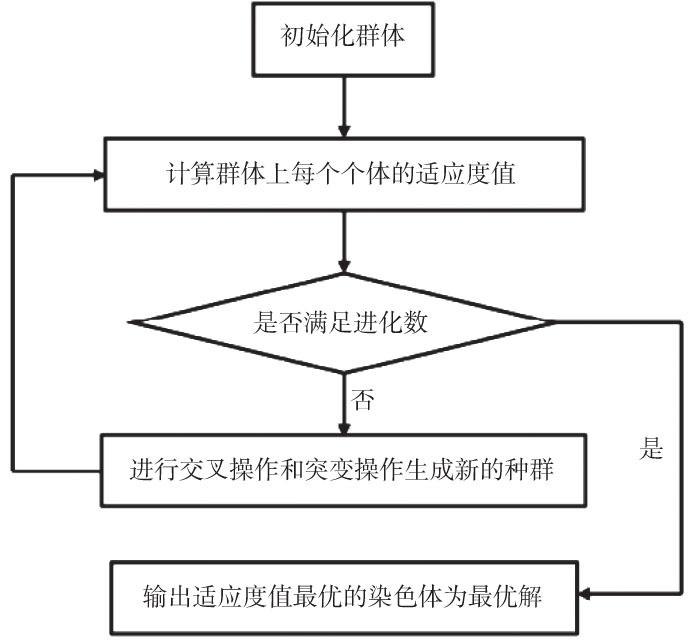
2.2 、优化算法分析
遗传算法广泛应用于工程实践,较其他算法,动静压轴承优化设计中遗传算法具有操作简单、适应性好的特点。遗传算法计算流程如图2所示。
图2 遗传算法计算流程
2.3 、优化计算
文中基于遗传算法,通过MATLAB对超高速磨削电主轴动静压轴承结构开展多目标优化设计。设定进油孔直径、初始油膜厚度、浅腔深度分别为X1、X2、X3,开展优化设计。计算结果显示,以上三项参数相互矛盾,因此优化迭代中难以获得最优解。经综合分析,确定最优非劣解集,该解集下设计变量取值范围为
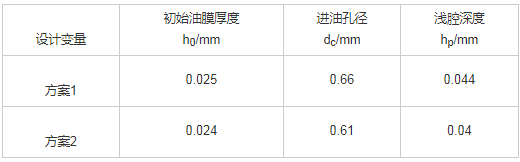
以最优非劣解集为基础,明确方案1和方案2的设计变量,并两个方案进行对比,结果如表2所示。
表2 设计变量比较结果表
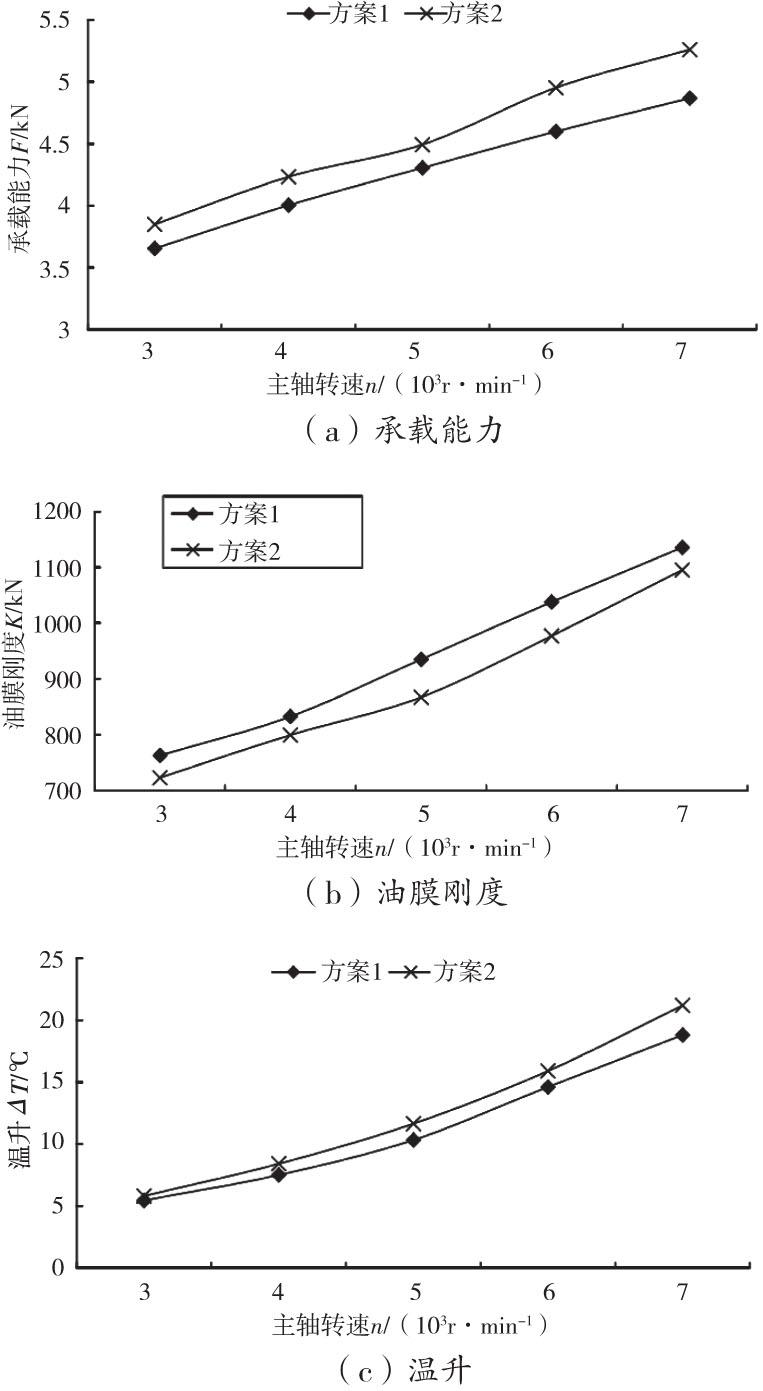
其他参数保持不变,主轴转速由3000 r/min提至7000 r/min, 供油油压为2 MPa, 油膜偏心率为0.2,两方案的油膜承载能力、刚度及温升变化曲线如图3所示。
图3为两方案设计中,承载能力、油膜刚度及温升与主轴转速之间的变化曲线。由图3可知,方案1中,轴承温升、油膜刚度及承载能力随着主轴转速的提升而提升,同时,油膜刚度及承载能力优于方案2,油液温升小于方案2,即在既定偏心率下,优化后动静压轴承油液温升、油膜刚度及承载能力均优于优化之前,所以,本文所开展的优化设计与预期目标相契合,同时,在优化效果上也十分突出。
图3 主轴转速对承载特性的影响
3 、结论
固定其他参数,取进油孔径、初始油膜厚度和浅腔深度三个参数为设计变量,以液体动静压轴承温升、油膜刚度和承载能力为设计目标,用遗传算法对其结构参数进行了多目标优化设计,经分析得到如下结论:
1)初始参数进油孔径dc为0.60 mm, 初始油膜厚度h0为0.025 mm, 浅腔深度hp为0.050 mm, 优化后的参数分别为0.65 mm、0.026 mm和0.045 mm;
2)优化后轴承的温升、油膜刚度及承载能力与主轴转速成正比变化;
3)优化后的轴承温升较优化前小,而油膜刚度和承载能力均大于优化前,证明了本文优化方法的可行性和有效性,达到了预期优化目标。
参考文献
[1]刘蕾,刘保国,王攀, 等.液体动静压轴承油膜的压力场和温度场分析[J] .机电工程, 2019,36(9):900-906 .
[2]云飞.气体润滑理论与气体轴承设计[M] .北京:机械工业出版社, 2016.
[3]郭胜安,侯志泉,能万里. 基于CFD的深浅腔液体动静压轴承承载特性研究[J] .制造技术与机床,2012(9):57-62 .
[4]吴怀超,令狐克均,孙官朝.基于遗传算法的高速轧辊磨床磨头液体动静压轴承的优化设计[J] .中国机械工程, 2017(18):2495-2500 .
[5]赵亚东,梁兴,张运真,等.复合式动静压轴承的结构设计及仿真分析[J] .制造技术与机床, 2019(1);:31-36 .
[6]孙靖,巩敦卫.进化高维多目标优化研究进展[J] .控制理论与应用, 2018,35(7):928-938.
[7]孟曙光,能万里,沙力,等.有限体积法与正交试验法相结合的动静压轴承结构优化设计[J] .中国机械工程, 2016,27(9):1234-1242.
[8]龙慎文,王优强,周亚博,等.水润滑螺旋阶梯腔动静压滑动轴承的优化分析[J] .机械传动, 2018,42(4):52-56.