对小型采样器的铲挖参数进行优化设计

　　0、引言

　　铲挖式月壤采样是对月探测活动中收集浅层月壤的重要手段。铲挖过程中，月壤对采样器存在阻力作用，其大小由月表重力、月壤力学特性和采样器结构共同决定。受探测器尺寸、铲挖驱动功率的影响，月壤采样器多采用小型化设计。为了高效、快速、低能耗地实现对月壤的收集，需要利用完善的铲挖阻力解析模型，对小型采样器的铲挖参数进行优化设计。

　　各国学者对铲挖阻力模型进行了大量的研究和试验，从土壤失效、颗粒流等不同方面对土壤挖掘阻力进行了细致分析。1964年，OsmanM等人提出曲线失效面的概念，建立了Osman模型，该模型精度较早期广泛使用的直线失效面模型提高很多;Gill/VandenBerg模型在前者基础上添加了土壤惯性力与内聚力，同时对机—土摩擦力进行了简化;Swick/Perumpral模型与McKyes模型，又分别针对二维推土板与土壤的切割过程，给出了铲挖阻力的不同数学表达式;Lockheed-Martin/Viking模型，针对斗轮式挖掘装置，提出了铲挖阻力与铲挖速度之间的非二次方关系的铲挖阻力方程。上述五种模型采用二维简化模型分析了其铲挖阻力。为考虑铲斗侧壁在铲挖过程中的切割和摩擦效应，一些学者也建立了三维铲挖阻力经验模型，典型代表有以下两种:(1)Hemami模型，将铲挖阻力分为斗内土壤重力、土壤压缩阻力、机—土滑移摩擦、推移切割阻力、土壤移动惯性力、铲挖斗移动惯性力等六种分力;(2)Balovnev模型，在前者基础上将公式中的推移切割阻力进行了进一步细化。

　　但是，由于成因及所处环境不同，月壤的力学性质与地面土壤存在较大的差异，导致传统的地面铲挖模型无法直接用于预测月壤的铲挖阻力。同时，对于目前研究月壤—机构交互作用中常采用的数值分析方法，由于计算量极大，也较难用于开展参数优化工作。因此，本文利用与真实月壤应力—应变试验结果相吻合的浅层月壤离散元模型，对月表环境下的月壤抗剪强度和弹塑性本构参数进行了分析，并将分析结果引入到基于McKyes模型和Kostritsyn公式的铲挖阻力模型中，建立了浅层月壤铲挖阻力预测模型。在此基础上，针对深空探测器机构小型化、轻量化的设计需求，本文基于预测模型对小型浅层月壤采样器的铲挖参数关系进行了研究，在综合考虑月壤铲挖阻力和收集速率的条件下，利用自适应遗传算法对不同铲宽参数下的最优铲挖角和最优铲挖深度进行了计算。

　　1、月壤力学性质研究

　　1．1月壤抗剪特性

　　基于线刚度颗粒接触理论定义月壤散体颗粒，利用文献中的月壤离散元细观参数，建立月壤离散元模型。

　　

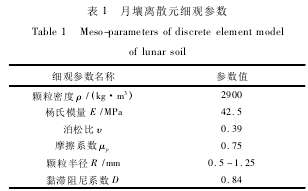
　　根据表1建立轴向长度12mm，宽度和高度均为6mm的月壤离散元模型，定义月表重力加速度g=1．63m/s2，设置围压σw并对月壤模型施加轴向应力，开展微型静三轴试验仿真。由于月表无大气，且所铲挖月壤均为浅层预应力较小的月壤，故σw较低。分别设计σw为35kPa、50kPa、65kPa、80kPa和95kPa共5种工况，对各工况下的月壤模型开展三轴压缩试验。保持轴向应变速率为0．003%/min，仿真结果如图1所示。

　　

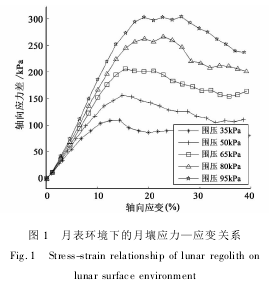
　　对上述5种围压下的月壤应力—应变曲线进行分析，利用月壤发生剪切破坏时的大、小主应力，基于莫尔—库仑强度理论计算月表环境下的浅层月壤抗剪强度如表2所示。

　　1．2月壤泊松比

　　在月壤三轴压缩试验中，定义εV为月壤体应变，εz、εw1和εw2分别为月壤轴向应变和两个横向应变，有εV=εz+εw1+εw2(1)由于三轴试验中εw1和εw2基本相等，定义υ为月壤泊松比，于是有υ=－εV－εz／2εz(2)利用图1所示5种围压下的月壤应力—应变曲线对υ进行计算。将月壤初始压缩阶段，即轴向应变εz=0．5%时的εV代入式(2)中，并对所有工况的计算结果取平均值，得月壤泊松比υ=0．549。

　　1．3月壤弹塑性本构

　　月壤具有弹塑性，其本构关系可通过一系列具有不同屈服极限的弹簧元件和摩擦元件所组成的Iwan机械模型进行描述，如图2所示。

 

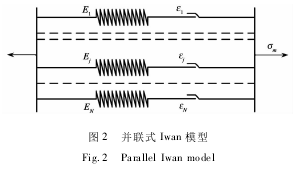
　　定义N为弹塑性元件总数，Ej为元件j的弹性模量，εj为元件j的屈服应变。对各弹塑性元件按屈服应变值的大小顺序递增排列，定义σm为月壤所受应力，当σm的加载作用导致月壤产生应变εm时，有

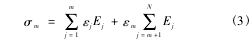
　　式中:m为月壤所受应力为σm时，发生屈服的弹塑性元件数量，m∈{1，2，…，N}。

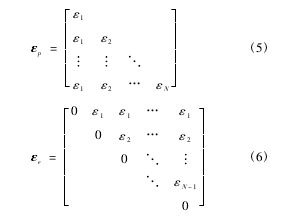
　　在一定的应变范围内布置N个弹塑性元件。上述N个元件各自的屈服应变取值均匀分布在设定的月壤应变范围内并逐个递增。根据式(3)，分别建立m为1到N时的月壤弹塑性本构模型并联立，有σ=(εp+εe)E(4）式中:应力阵σ=［σ1，σ2，…，σN］T，弹性模量阵E=［E1，E2，…，EN］T，εp为塑性应变阵，εe为弹性应变阵。εp和εe如式(5)、式(6)所示。

　　采用动三轴试验方法确定各应力阵σ，进而实现对弹性模量阵E的求解。以1．1节中月壤模型为仿真试验样本，保持围压30kPa，并对月壤施加轴向应力，开展微型动三轴试验仿真。设计施加在月壤轴向的正弦型应力为σf，有σf(t)=Asin(2πt/T)+σd(7)式中:σd为偏压固结轴向应力，T为应力周期，A为应力幅值。

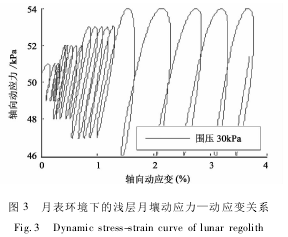
　　对月壤施加σd=50kPa的偏向固结压力，轴向动应力σf周期T为50s。加载过程分为4级，每级各加载5个周期，各级幅值A分别为1kPa、2kPa、3kPa、4kPa。仿真结果如图3所示。

　　根据图3仿真结果，移除月壤动三轴应变累积值，并定义σf各级第3周期的动应力—动应变曲线为参考回滞圈，根据各回滞圈顶点的动应力和动应变幅值，绘制月壤骨干曲线如图4所示。

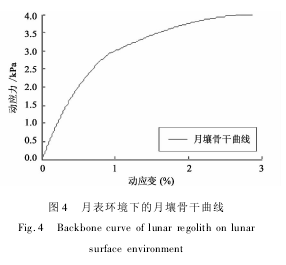
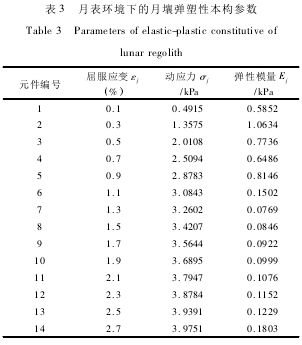
　　根据图4的月壤骨干曲线，定义弹塑性元件总数N=14，分别对14个元件的屈服应力σ进行计算，并将其代入到式(4)中，求解得浅层月壤弹塑性模型的弹性模量阵E如表3所示。

　　将E代入式(3)中，定义y为月壤正应变，当y为加载特性时，有月壤正应力σ=I(E，y)=［ε1，…，εm，y，…，y］E(8)式中:ε1，…，εm为应变小于y的弹塑性元件屈服应变。

　　同理，定义ζ为剪应变，将月壤泊松比υ代入式(8)中，得月壤剪应力τ，有τ=I(G，ζ)=I（E/2(1+υ)，ζ）(9）

　　2、月壤铲挖阻力预测模型

　　2．1铲挖阻力分析

　　受月壤重力、月壤抗剪强度和机—土摩擦作用的影响，采样器铲斗在工作过程中会存在铲挖阻力。

　　如图5所示，月壤铲挖阻力由铲斗侧壁切削阻力F和底面推移阻力T组成。设计铲斗牵引速度方向保持水平，铲挖全过程中，铲斗底面与水平面保持铲挖角β并沿牵引方向对月壤产生推移作用;铲斗侧壁在铲挖全程与水平面保持垂直并沿牵引方向对月壤进行纯切削。

　　

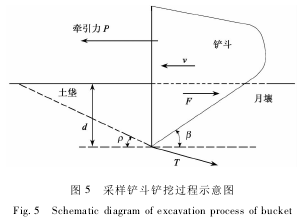
　　定义月壤水平铲挖阻力为RH，建立月壤铲挖阻力预测模型有RH=Tsin(β+δ)+2F(10)式中:δ为机—土摩擦角。

　　2．2底面推移阻力分析月壤铲挖时的底面推移阻力T。采样器铲斗的底面前方月壤在推移作用下会形成月壤土垡，底面推移阻力T即由土垡重力、土垡—原位月壤间的抗剪作用、土垡—铲斗底面摩擦力和土垡惯性力共同作用而成。基于McKyes机—土静力平衡方程建立采样器铲斗底面推移阻力模型，有

 

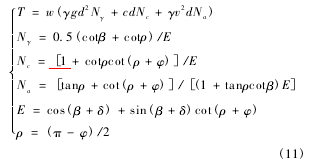
　　式中:w为铲斗宽度，γ为月壤密度，g为月表重力加速度，d为铲挖深度，c为月壤内聚力，v为铲斗牵引速度，β为铲挖角，ρ为月壤滑裂面倾角，φ为月壤内摩擦角，δ为机—土摩擦角。

　　将表2中月表环境下的月壤抗剪强度仿真结果，即内聚力c=0．5145kPa和内摩擦角φ=39．736°代入式(11)中，得月壤采样器的铲斗底面切削阻力模型。

　　2．3侧壁切削阻力

　　分析月壤铲挖时的侧壁切削阻力F。根据Kostritsyn公式，侧壁板沿月壤沿切削方向的纯切削阻力为

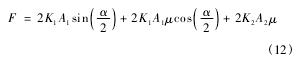
　　式中:K1为刃面处月壤变形比阻，K2为板面处月壤变形比阻，A1为月壤—刃面接触面积，A2为月壤—板面接触面积，α为刀口刃角，μ为机—土摩擦系数。

　　

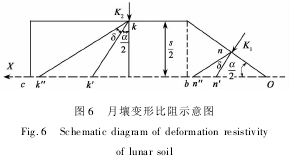
　　对月壤的变形比阻进行分析。一方面，在切削月壤过程中，侧壁板施加在月壤上的作用力使月壤产生局部变形，从而导致月壤切削面对侧壁板存在压力作用。如图6所示，定义原点O为壁板刃尖，切削反方向为X正向，s为壁板厚度，通过对壁板表面n和k点的月壤颗粒运动轨迹可知，刃面x位置的月壤变形量Ln　为

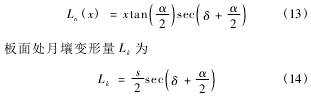
　　另一方面，受月壤自身重力作用的影响，月壤的预应力随深度的增加而不断增大。该预应力导致了月壤在垂直于壁板刃面的方向存在初始应变εI。

　　由于该预应力对月壤呈现加载特性，故利用式(8）分析深度h处的月壤初始应变εI，有

 

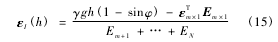
　　式中:εm×1为发生屈服的前m个弹塑性元件的屈服应变子矩阵，Em×1为发生屈服的前m个弹塑性元件的弹性模量子矩阵，Em+1，…，EN分别为未发生屈服的N－m个弹塑性元件的弹性模量。将变形比阻的计算转化为基于月壤弹塑性本构模型的半空间问题，定义n为月壤形变方向，η为月壤形变量，f为刃面压力，联立月壤的基本微分方程、应力边界条件及平衡方程，有

　　对壁板刃面处的月壤变形比阻K1和板面处的月壤变形比阻K2进行分析。由于切削过程中壁板对月壤不断挤压，故该位置的月壤应变呈现加载特性。考虑月壤初始应变εI，结合式(15)和式(16)，采用数值方法对ηn=Ln(x)和ηn=Lk时的f进行计算，得壁板的机—土接触面各位置的月壤变形比阻为

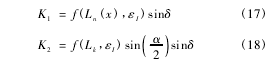
　　分析铲斗侧壁板对月壤的切削过程，如图7所示。定义b为侧壁板刀刃长度，且切削深度h与侧壁板长度x间存在x=x(h)，则侧壁切削阻力F为

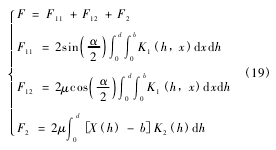
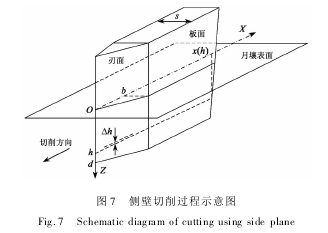
　　式中:F11为刃面月壤推移阻力，F12为刃面月壤摩擦阻力，F2为板面月壤摩擦阻力。

　　3、铲挖参数优化设计

　　3．1铲挖优化方案

　　根据式(10)，在给定采样器铲宽w的条件下，铲挖深度d、牵引速度v和铲挖角β是决定月壤铲挖阻力RH的3个重要影响参数。其中，d、v的减小会导致RH的变小;β的减小会导致RH先变小后变大。

　　另外，采样任务的风险性和不可预知性使对月壤的铲挖过程需在尽可能短的时间内完成。定义月壤样本收集速率V，有V=vwd(20)分析可知，d、v的减小在降低RH的同时，也带来了V减小的劣势。为了解决月壤高效率铲挖中关于较大的V与较小的RH之间的冲突，有必要利用多目标优化理论对铲挖参数进行优化设计。

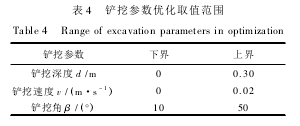
　　考虑采样机构整体尺寸大小及安装放置条件，以典型的凤凰号(Phoenix)探测器采样铲斗的工作参数为参考，设计待优选铲挖参数d、v和β的决策变量集X如表4所示。

　　根据多目标优化问题(MOP)，以月壤收集速率V和月壤铲挖阻力RH为目标对铲挖参数进行优化，通过调整d、v和β，使RH尽可能小，V尽可能大。设计目标函数为

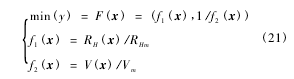
　　式中，x=(d，v，β)∈X;Vm为决策变量范围内的最大月壤样本收集速率;RHm为决策变量范围内的最大月壤铲挖阻力。

　　采用权函数法对F(x)进行处理，分别对f1和f2给出权系数λ1和λ2，有优化评价函数U=U(λ1f1(x)+λ2f2(x))(22)式中，λ满足λ1+λ2=1，λ1，λ2＞0。

　　3．2基于动态算子概率的寻优策略

　　采用动态算子概率的自适应遗传算法对月壤采样时的铲挖参数进行优选，根据种群进化过程中目标函数相似度的变化，对交叉概率和变异概率进行实时调整，保证优选结果能够收敛至全局最优解。定义i为种群进化代数，采用相似系数κ描述第i代种群中各目标函数值的相似程度，有

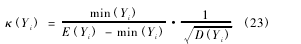
　　式中，Yi为第i代的种群目标函数值集合。随着进化代数i的增大，Yi的期望值和方差逐渐变小，相似系数κ逐渐变大，种群个体差异变小，进化趋向收敛。定义种群个体交叉算子概率Pc的变化范围为［0．4，0．9］，变异算子概率Pm的变化范围为［0，0．1］，建立以Logistic方程为基础的调节公式，如式(24)所示。

　　

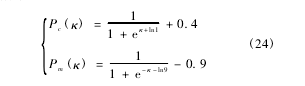
　　4、仿真算例

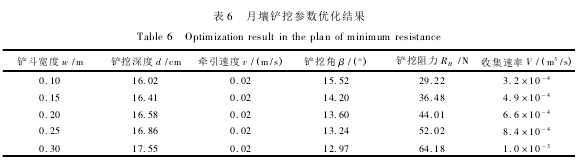
　　设计采样器铲宽w分别为0．1m、0．15m、0．2m、0．25m和0．3m，以式(22)为优化评价函数，采用基于动态算子概率的自适应遗传算法对月壤铲挖角β、月壤铲挖深度d和铲斗牵引速度v进行优化，各决策变量取值范围如表4所示。考虑月壤采样任务中以铲挖阻力RH为主要指标，月壤样本收集速率V为次要指标，定义目标函数权系数λ1=0．6，λ2=0．4。

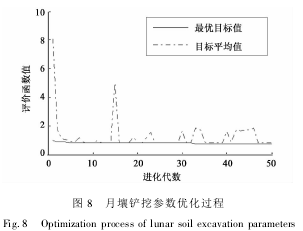
　　根据表5所示的自适应遗传算法参数对月壤铲挖参数进行优化。图8显示了铲宽w=0．3m条件下的铲挖参数优化过程。优化结果表明，5个铲宽条件下的铲挖参数均收敛至最优解。

　　

　　由表6中的最优牵引速度计算结果可以看出，不同的铲宽条件下，铲斗牵引速度v均为优化取值范围上限，说明针对小尺寸采样器的浅层月壤铲挖，v对铲挖阻力RH的影响不大。通过对月壤铲挖阻力的分析可知，v是铲斗底面推移阻力T中月壤土垡惯性力部分的重要影响因素，但由于浅层月壤小尺寸铲挖条件下，月壤土垡总质量较小，从而月壤土垡惯性力远小于T中的其他组成部分，最终导致v对铲挖阻力RH的影响不大。

　　另外，由表6中的最优铲挖深度d和月壤铲挖角β可以看出，各个铲宽条件下均存在一个β和d的最优值，且随着w从0．1m增加至0．3m，β的最优值逐渐由15．52°递减至12．97°，而d的最优值逐渐由16．02cm递增至17．55cm。

　　5、结论

　　本文利用离散元法建立了浅层月壤的Iwan弹塑性本构方程，通过基于Kostritsyn土壤纯切削公式和Mckyes机—土静力平衡方程，分别对采样器铲斗经过计算，各个铲宽条件下的最优铲挖参数、月壤铲挖阻力和月壤收集速率如表6所示。

　　

　　侧壁切削阻力和底面推移阻力进行了分析，建立了浅层月壤铲挖阻力预测模型。在此基础上，利用该预测模型，对铲宽小于0．3m的小型铲挖式采样器的浅层月壤最优铲挖参数进行了优化，得到结论如下:

　　(1)针对小尺寸浅层月壤采样器，其牵引速度对铲挖阻力影响不大，但可有效增加样本收集速率，因此铲斗牵引速度可在驱动机构及控制器允许的前提下适度增大。

　　(2)综合考虑铲挖阻力和样本收集速率，小尺寸浅层月壤采样器的最佳月壤铲挖深度约在16cm～18cm范围内，并随着铲斗宽度的增大略有增加。

　　(3)月壤采样器最佳铲挖角约在12°～16°范围内，并随着铲斗宽度的增大逐渐降低。

　　以上工作对以浅层月壤为对象的铲挖阻力开展了分析，并对采样过程中的最优铲挖参数进行了计算。上述结论对机器人自主采样，特别是针对我国在月球二、三期探测计划中关于小型无人月壤采样器的研制，具有一定的工程参考价值。

　　参 考 文 献：
　　［1］ 卢伟，宋爱国，凌云． 面向浅层月壤的小型取样器研究［J］．宇航学报，2011，32( 9) : 2065 － 2073． ［Lu Wei，Song Ai-guo，Ling Yun． Research on the sampler for shallow lunar regolith［J］． Journal of Astronautics，2011，32 ( 9 ) : 2065 －2073．
　　［2］ Osman M． The mechanics of soil cutting blades［J］． Journal of Agricultural Engineering，1964，9( 4) : 313 － 328．
　　［3］ Gill W，VandenBerg G． Agriculture handbook no． 316［M］．Washington DC: Agricultural Research Service，US Department of Agriculture，1968．
　　［4］ Swick W C，Perumpral J V． A model for predicting soil-tool interaction［J］． Journal of Terramechanics，1988，25( 1) : 43 －56．
　　［5］ McKyes E． Soil cutting and tillage［M］． Amsterdam: Elsevier，1985．
　　［6］ Muff T，King R H，Duke M B． Analysis of a small robot for Martian regolith excavation［C］． AIAA Space 2001 Conference ＆Exposition，Albuquerque，USA，August 28 － 30，2001．
　　［7］ Hemami A，Daneshmend L． Force analysis for automation of the loading operation in an LHD-loader［C］． IEEE International Conference on Robotics and Automation，Nice，France，May 12－ 14，1992．
　　［8］ Balovnev V I． New methods for calculating resistance to cutting of soil［M］． New Delhi: Amerind Publishing Company，1983．
　　［9］ Perkins S，Madson C． Mechanical and load-settlement characteristics of two lunar soil simulants［J］． Journal of Aerospace Engineering，1996，9( 1) : 1 －9．
　　［10］ 梁东平，柴洪友． 着陆冲击仿真月壤本构模型及有限元建模［J］． 航天器工程，2012，21( 1) : 18 － 24．［Liang Dong-ping，Chai Hong-you． Lunar soil constitutive model and finite element modeling for landing impact simulation ［ J ］． Spacecraft Engineering，2012，21( 1) : 18 － 24．］
　　［11］ 卢波． 21 世纪空间探测的发展趋势及其小型化技术研究［C］． 中国空间科学学会空间探测专业委员会第十五次学术会议，安徽池州，2002 年 10 月．
　　［12］ 任子武，伞冶． 自适应遗传算法的改进及在系统辨识中的应用研究［J］． 系统仿真学报，2006，18( 1) : 41 －66．［Ren Zi-wu， San Ye． Improved adaptive genetic algorithm and its　application research in parameter identification［J］． Journal of System Simulation，2006，18( 1) : 41 － 66．
　　［13］ 李伟，朱德懋，胡选利，等． 不连续散粒体的离散单元法［J］． 南京航空航天大学学报，1999( 1) : 85 － 91．Li Wei，Zhu De-mao，Hu Xuan-li，et al． Discrete element method of discontinuous granular media［J］． Journal of Nanjing University of Aeronautics ＆ Astronautics，1999( 1) : 85 － 91．
　　［14］ 邹猛． 月面探测车辆驱动轮牵引性能研究［D］． 长春: 吉林大学，2008． ［Zou meng． Study of traction ability for driving wheel of the Lunar rover［D］． Changchun: Ji Lin University，2008．
　　［15］ Iwan W D． On a class of models for the yielding behavior of continuous and composite［J］． Journal of Applied Mechanics，1967，34( 3) : 612 － 617．
　　［16］ Kostritsyn A K． Resisance of soil to tillage tools of soil-working implements ［M］． Washington DC: Al Ahram Center for Scientific Translations，1981．
　　［17］ Smith P H，Tamppari L，Arvidson R E，et al． Introductin to special section on the Phoenix Mission: landing site characterization experiments，mission overviews，and expected science［J］． Journal of Geophysical Research: Planets ( 1991 －2012) ，2008，113( E3) : 2156 － 2202.