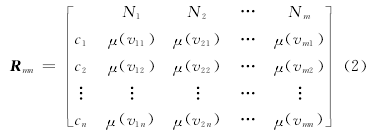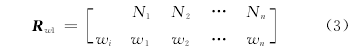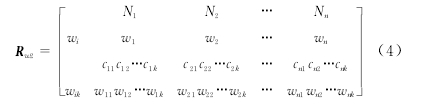在建立树型模型库时,遵循以下规则。
规则1:每个节点上都有相应的评价模型,且所有节点上评价模型的评价能力互不相同。
规则2:如果存在左右子树,则左右子树所有节点上模型的评价能力都小于根节点上模型的评价能力。
规则3:所有左节点上模型的评价能力均大于右节点上模型的评价能力。
规则4:左子树模型和右子树模型也是评价模型库。
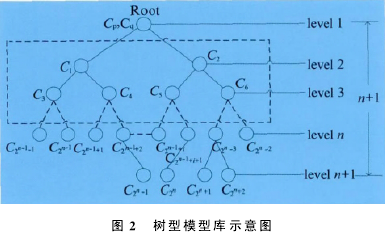
基于上述规则,以元模型作为树型模型库的根(Root),以元模型的评价能力为中心,求出各模型相对于元模型评价能力的距离。对上述距离进行归一化处理,即为各模型与元模型评价能力的关联度,同时得到关联度区间[Rmin,Rmax].选择两个关联度最大的模型作为元模型的子模型(Level 2水平),且满足在树型结构中左节点上模型的关联度>右节点上模型的关联度。
按如下算法选择Level 2下方的子模型:以左节点上的模型为中心,求出剩余各模型相对于左节点上子模型评价能力的距离;对所得到的距离进行归一化处理,即为剩余各模型与左节点上子模型评价能力的关联度;选择两个关联度最大的模型作为左节点上模型的子模型。以右节点上的模型为中心,求出剩余各模型相对于右节点上模型评价能力的距离;对该距离进行归一化处理,即为剩余各模型与右节点上模型评价能力的关联度;选择两个关联度最大的模型作为右节点上模型的子模型。重复上述过程,直至所有模型都被放入树型模型库的节点上,如图2所示。
图2所示树型结构模型具有如下性质。
性质1:若树型模型库的层次从1开始,则在模型树的第i层最多有2i-1个节点。
性质2:高度为k的模型树最大节点数为2k-1.
性质3:对于任何一棵模型树,如果其叶节点个数为n0,度为2的非叶节点个数为n2,则有n0=n2+1.
对第3条性质进行证明:统计树中节点的总数为n,设树中度为1的节点个数为n1,因为树只有度为0、度为1和度为2的节点,所以树中节点总数n=n0+n1+n2;树中分支条数(边数)为e,因为树中根节点没有双亲节点,边数为0,其它每一结点都有且只有一个双亲节点,边数各为1,所以二叉树中总边数e=n-1=n0+n1+n2-1;由于每个度为2的节点发出2条边,每个度为1的节点发出1条边,度为0的节点发出0条边,因此总边数e=2n2+n1;将两个关于边的等式联立,有n0+n1+n2-1=2n2+n1,得n0-1=n2,即n0=n2+1.
2.4二叉树模型的权重。
用R表示审查资料各影响因素的特征矩阵,N表示影响资料审查的各因素,c表示各个时刻,μ(v)表示资料审查各因素c相应量值v的隶属度,由m个因素N、n个时刻(c1、c2、…、cn)、评价量值μ(vxj)(x=1,2,…,m;j=1,2,…,n)构成的阵列为:
Rmn称为资料审查的特征矩阵。
若以Rw表示影响每一评价资料各项因素的权矩阵,并以wi(i=1,2,…,n)表示每一资料第i项因素的权重,则有一层关联权特征矩阵:
具有若干层次影响因素的资料审查,对应的权重也分为若干层,以两层为例,两层关联权特征矩阵为:
式(4)中cik表示资料审查影响层次模型中第i项主要影响因素所属的第k项次要影响因素,与其对应的权重用wik(i=1,2,…,n)来表示。其余层次关联权特征矩阵可依次类推。