铅套和铜皮对弹丸侵彻钢管混凝土的作用

　　钢管混凝土在高层建筑和桥梁中已得到较广泛应用，但对于其抗侵彻方面的研究目前还较少。甄明等采用 12.7mm 穿甲弹进行了外径 140mm、壁厚 3.5mm、靶厚 300mm 钢管混凝土厚靶侵彻试验；运用 Ansys/Ls-dyna 软件，弹丸按钢芯、铜皮、铅套完整弹建模，对试验内容进行了相应数值模拟，并探索了外径和壁厚对钢管混凝土靶体抗侵彻性能的影响。研究表明，钢管约束混凝土具有优越的抗侵彻性能。

　　为提高计算效率，本文在文献[4]的基础上，删去了数值计算模型中弹丸的铜皮和铅套部分，仅按刚性钢芯建模，对钢管混凝土侵彻试验部分工况进行了数值模拟，对比分析了铅套和铜皮对弹丸侵彻钢管混凝土在侵深和靶体损伤等方面的影响，表明本文弹丸模型简化合理可行。

　　1 计算模型及材料模型

　　为保证对比的有效性，本文弹、靶计算模型及材料模型与文献[4]一致。考虑对称性仍取实体模型的1/2 进行建模，在对称面上定义对称边界条件来约束网格节点的自由度弹丸为 12.7mm 穿甲燃烧弹，其完整结构如图 1 所示，在本文中仅保留钢芯来进行数值模拟。钢芯采用刚体材料模型，密度为 7850 kg/m3，泊松比取 0.3。钢管混凝土靶厚 300mm，外径 140mm，钢管壁厚 3.5mm。采用传统Lagrange网格与光滑粒子相结合的方法建模，靶体混凝土在以弹着点为中心，半径为25mm的圆柱形区域内采用间距 1.5mm 光滑粒子，如图 2 所示。【图1-2】

　　
　　靶体混凝土采用连续帽盖模型，模型中两个关键参数单轴抗压强度和最大骨料粒径仍分别取48.9Mpa 和 8mm。钢管采用弹塑性随动硬化材料模型，模型参数同文献[4]。弹丸钢芯与光滑粒子区之间采用点-面侵蚀接触。混凝土 Lagrange 网格区与光滑粒子区之间采用点-面连接接触，与钢管内壁接触面按固结处理，不考虑滑移。

　　2 数值模拟结果及分析

　　参考文献[4]试验结果，利用上面确定的计算模型和材料模型，对弹着点为靶体迎弹面中心、侵彻速度分别为 540.9m/s 和 833.3m/s 以及弹着点偏心 15mm、侵彻速度为 838.2m/s 的三种侵彻工况分别进行了完整弹侵彻和钢芯侵彻数值模拟，各工况最终侵深和漏斗坑大小如表 1、2 所示。【表1.表2】


　　
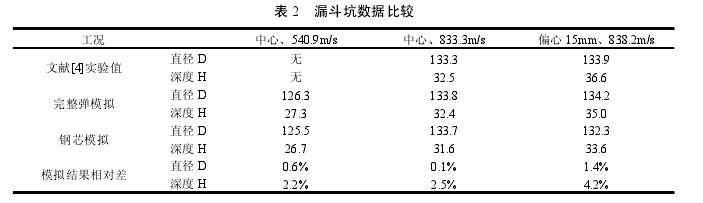
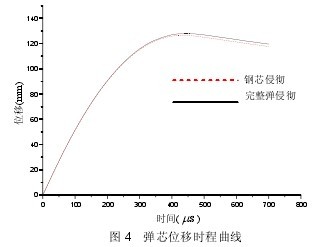
　　由表可知，弹丸有无铅套和铜皮对靶体最终侵深和漏斗坑大小影响很小。在完整弹丸侵彻情况下，由于总质量较大，弹丸总动能较大，且铜皮和铅套先作用于混凝土会对其造成预损伤，因此靶体的最终侵深和漏斗坑较大，但跟仅利用钢芯侵彻情况相比总体误差都在 5%以内。图3给出了中心侵彻、速度为540.9m/s工况下靶体的最终损伤云图。由图可知，利用完整弹丸侵彻和仅利用钢芯侵彻靶体混凝土损伤情况基本一致，二者混凝土内部损伤程度和范围以及环向主裂纹位置差别很小，靶体背面混凝土基本不受影响。图 4 和图 5 分别给出了中心侵彻、速度为 540.9m/s 工况下弹芯的位移时程曲线和速度时程曲线。由图可知，钢芯的运动基本上都经历了匀速、减速和回弹三个阶段，在弹丸有铅套和铜皮情况下，靶体混凝土因受到预损伤从而对弹芯施加阻力较小，弹芯位移较大，速度减小较快。【图3-5】


　　
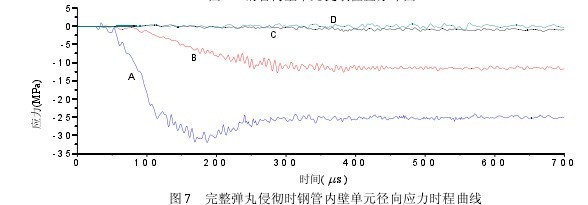
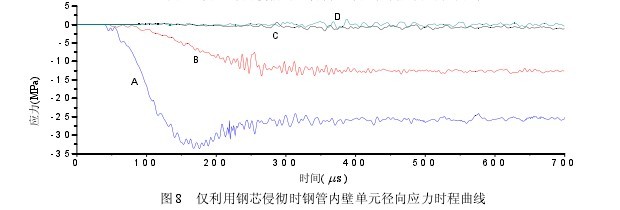
　　为研究钢管对混凝土的约束作用，提取中心侵彻、速度 540.9m/s 工况下钢管内壁不同位置单元的径向应力时程曲线，对其径向应力变化情况进行分析。所提取单元位置分布如图 6 所示，径向应力时程曲线如图 7 和图 8 所示。由图可知，在完整弹丸侵彻和仅利用钢芯进行侵彻两种情况下，钢管内壁相应单元都产生了径向压应力，且从迎弹面到靶体背面依次减小。A、B、C、D 四点处单元在两种情况下的径向压应力大小和波动规律基本一致，其中 A、B 处单元因离混凝土损伤区较近，其应力曲线均表现为一个明显的上升阶段和一个稳定阶段，而 C、D 处单元应力曲线则一直较平缓。以 A 点单元为例进行应力分析：弹丸接触混凝土后产生弹性压缩波，压缩波在达到钢管壁后会反射成拉伸波，二者作用重合，导致应力曲线呈振荡变化状态。在有铅套和铜皮作用情况下，弹体由于材质不同且能量较大，又因建模时混凝土与钢管壁之间采用的是固结处理，故应力曲线在 30 处会出现一个较小的拉力峰值。随着弹丸侵深的增加，前一侵彻阶段混凝土会逐步形成漏斗坑或隧道区，混凝土因受挤压作用减小产生形变恢复，从而对钢管壁产生拉力，故应力曲线在达到最大值后呈减少趋势。同样，在有铅套和铜皮作用情况下，因弹丸体积较大，侵彻混凝土后留下的穿透空间较大，混凝土形变恢复时产生较大回复拉力，因此 A 点处单元最大径向压应力比无铅套和铜皮的情况下小，但两种情况下的最终径向应力值差别不大。【图7-8】


　　
　　3 结论

　　本文在文献[4]试验和数值模拟研究基础上，简化弹体模型，仅利用弹芯进行小直径钢管约束混凝土侵彻数值模拟。结果显示：靶体的最终侵深、漏斗坑形状以及混凝土内部损伤和环向裂纹与弹体有无铅套和铜皮关系不大，因此在针对侵深等特定对象进行数值研究时，可以按照本文的思路设计弹丸模型，提高效率，减少工作量。

　　参考文献：

　　[1] 王世伟. 钢管混凝土的特点和研究应用现状[J]. 四川建筑, 2003, 23(5): 39—42.
　　[2] 蔡绍怀. 现代钢管混凝土结构[M]. 北京: 人民交通出版社, 2003.
　　[3] 石少卿, 黄翔宇, 刘颖芳, 康建功. 多边形钢管混凝土短构件在防护工程中的应用[J]. 混凝土, 2005(2): 95—98.
　　[4] 甄明. 有限空腔膨胀理论及约束混凝土抗侵彻机理研究[D]. 长沙: 国防科学技术大学, 2013.
　　[5] LS-DYNA KEYWORD USER'S MANUAL [M]. Version 971, Livermore Software Technology Corporation, 2007.