摘 要: 对于投篮问题的研究, 往往在无人防守的理想状态下, 对投篮的技术动作、篮球的运动轨迹、投篮角度等方面进行讨论。而实际比赛中, 后卫往往是对方的重点防守对象, 很难有空位出手的机会, 防守球员一般会用手臂挡住对方视线, 使投篮者起跳后无法看到篮筐, 这就需要我们对无人防守的理想状态下的模型进行改进, 为后卫重新设计一个最佳出手点和出手角度。本文首先研究投篮运动的普遍规律, 建立数学模型。然后考虑有人防守的情况下, 对模型进行改进, 从而提高命中率。
关键词: 防守状态; 投篮角度; 投篮命中率; 入篮角;

Abstract: The research on the shooting problem is often discussed in the ideal condition of undefended, the technical movement of the shot, the track of basketball, the Angle of shooting and so on.The actual competition, the defender is often the other side of the key defense objects, it is difficult to have the chance to shots, defensive players tend to use arm to protect each other's line of sight, make people can't see the basket after takeoff shooting, this needs us to the unmanned defense under the ideal state of model was improved, for the defender to design an optimal point and Angle.This paper first studies the general rule of the shooting movement and establishes the mathematical model.Then, the model is improved to improve the shooting rate when someone is defending.
Keyword: Shooting Angle; shooting average; Come in for the Angle;
一、问题分析
问题:有人防守时, 如何重新选择空心投篮的最佳投篮点及投篮角度。
在有人防守情况下, 采取干拔跳投的技术手段, 可以增加垂直高度, 假设速度不变, 使投篮的最佳角度减小, 可找到最佳出手点, 或者增加垂直高度, 假设投篮角度不变, 投篮速度变小;采取后仰跳投的方式, 延长水平距离, 增大投篮角度, 从而提高命中率。
二、模型假设
假设空气的阻力、主观因素对运动员投篮影响、篮球出手后球自身的旋转可忽略;假设篮球的运动轨迹和篮筐中心在同一平面内。
三、符号说明
表1
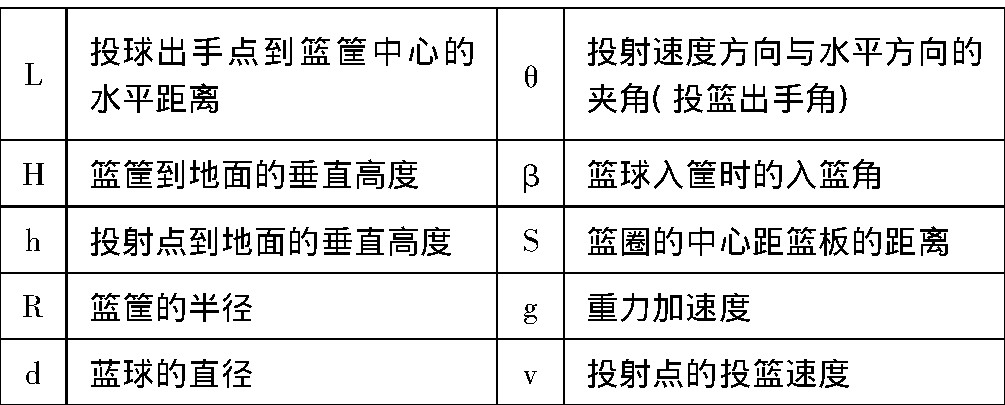
按照国际标准尺寸, L=4.6m, H=3.05m, d=24.6cm, D=45cm
四、模型建立与求解
(一) 用运动学知识建立最基础的投篮模型
t=0时刻, 篮球被投出, 出手时篮球的速度为v, 速度方向与水平面夹角为θ可得:
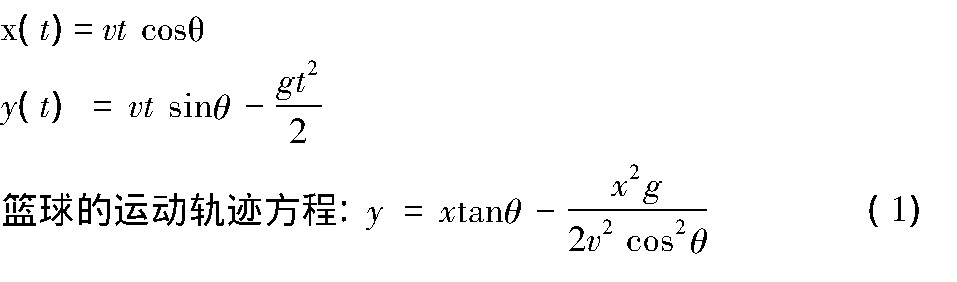
(二) 问题:有人防守时, 如何重新选择空心投篮的最佳投篮点及投篮角度
考虑到有人防守的情况下, 对模型进行改进, 例如后卫可以采取干拔跳投的方式, 增加垂直高度, 在速度不变的情况下使投篮的最佳角度减小, 提高命中率;采取后仰跳投的方式, 延长水平距离, 增大投篮角度, 从而提高命中率。
相关参数表
表2
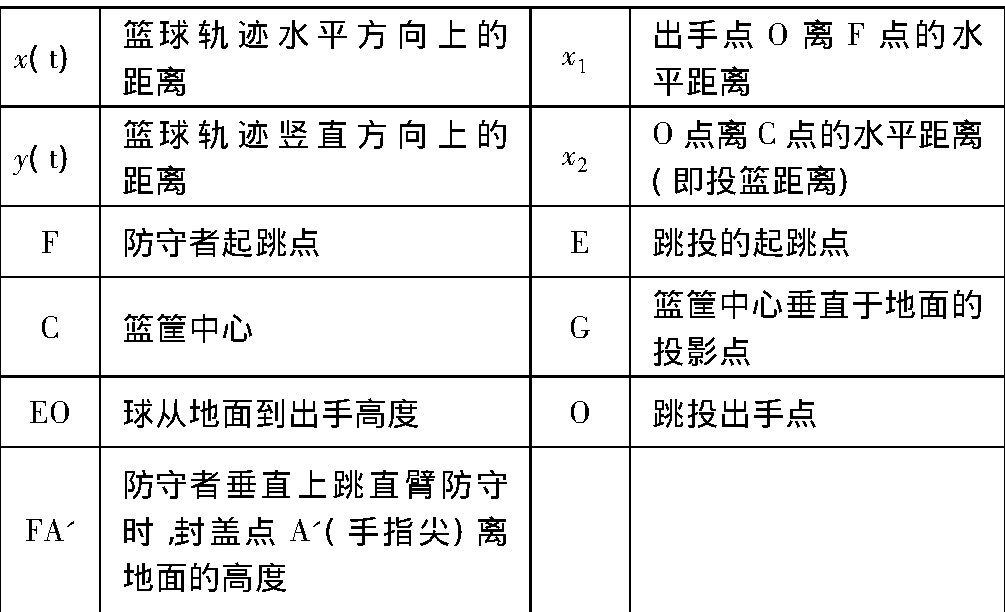
按照国际标准尺寸, L=4.6m, H=3.05m, d=24.6cm, D=45cm
投篮时有人防守的条件下, 投者跳投时, 能否免遭封盖, 决定FA与FA'的高度大小的关系, 即FA必须大于FA'。因A点是球心经过守者正上方时的轨迹点, 而球的半径为12.4cm, 当球经过A点时, 球的最下沿则比A点低12.4cm, 因此要免遭封盖, 使防守者触及不到球, 可得:

式 (6) 是在有人防守的条件下, 进行个人攻击跳投时, 免遭封盖的二维空间参数模型 (不考虑空气助力和球自身旋转对球的飞行轨迹的影响) 。
在测得或给定各种八通的有关参数 (EO、y2、θ、x2、x1) 值时, 则可根据式 (6) 计算出相应的各种y1值和FA值, 并可列成数表 (如表3) 。
表3
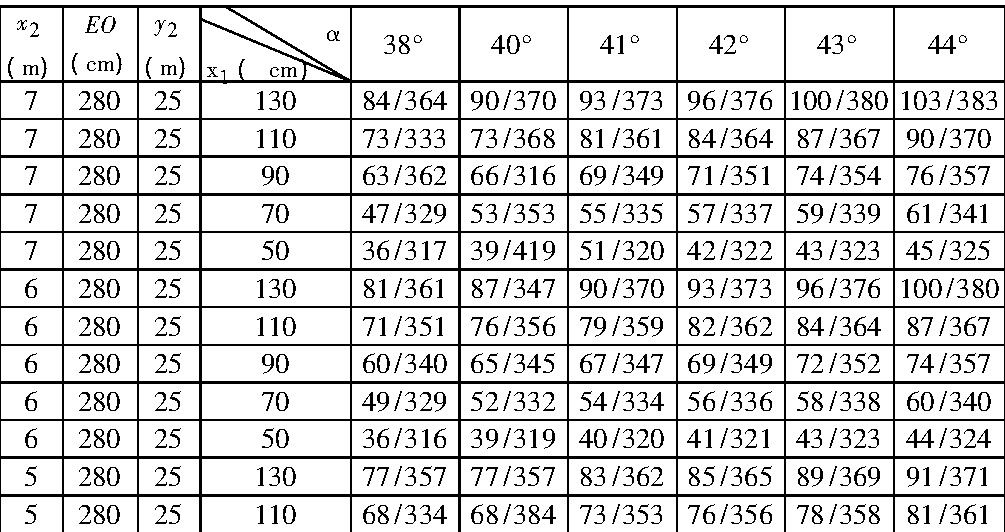
对数据的分析可知, 防守人员的身高及最大垂直高度是一个相对稳定的常量, EO是干拔跳投的出手点O的高度, EO越高, 免遭防守的水平 (即FA越高) 。同时y1的主要影响因素为θ, 与y1成正比, 当θ增加5°时:近投 (3-4米) y1可增加6-21cm;中投 (5-6米) , y1可增加7-24cm;远投 (7米) , y1可增加8-25cm;即θ的大小对y1的影响较大, 是避免防守的主要原因之一。在选定θ时, 还应考虑与命中率有关的入篮角, 允许误差范围等因素, 即要选定最佳θ。
其它因素不变的情况下x1越远, 则y1越高, 免遭防守水平也就越高, 当x1增加40cm时:近投 (3-4米) y1可增加12-38cm;中投 (1米) , y1可增加19-44cm;远投 (7米) , y1可增加24-46cm, 即x1大小对y1影响最大。
五、结论
经过对数据的分析和计算, 我们可以得出以下结论:组织后卫在有对方球员防守时, 投篮角度在45度左右时为最好, 若采取后仰跳投, 后仰角度一般在30度左右。在有人防守情况下, 采取干拔跳投的技术手段, 可以增加垂直高度, 假设速度不变, 使投篮的最佳角度减小, 可找到最佳出手点, 或者增加垂直高度, 假设投篮角度不变, 投篮速度变小;采取后仰跳投的方式, 延长水平距离, 增大投篮角度, 从而提高命中率。
六、模型评价与推广
本文所用的模型是建立在防守投篮得分的基础上, 通过对影响投篮各个因素进行详细分析, 给出了队员不同投篮速度和不同的投篮角度情况下提高投篮命中率对投篮角度和投篮速度的要求。建立的模型能与实际紧密联系, 推广性较强。
参考文献:
[1]张宏杰, 陈钓.篮球运动[M].北京:北京体育大学出版社, 2004:11-15.
[2]川川.投篮问题的数学建模.百度文库, 2012.
[3]苏之品.篮球投射的数学模型.
[4]赵凯华, 罗蔚茵.力学[M].北京:高等教育出版社, 2004:26-27.
[5]沉继红, 等.数学建模.哈尔滨工程大学出版社, 1998.
[6]肖宇谷.数学.北京:中国财经经济出版社, 2010.
[7]郭鼎文.投篮的技巧[M].北京:北京体育大学出版社, 2017.