葡萄酒质评的数学建模分析

　　摘    要：　已知酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系, 葡萄酒和酿酒葡萄监测的理化指标会在一定程度上反映葡萄酒和酿酒葡萄的质量等条件, 建立模型解决问题。文章主要通过正态分布、方差检验, 建立主成分分析、多元线性回归、聚类分析、相关系数和逐步回归模型来解决问题。

　　关键词：　葡萄酒; 正态分布; 主成分分析; 多元线性回归; 聚类分析;

　　Abstract：　It is known that the quality of wine grapes has a direct relationship with the quality of the wines being brewed. The physical and chemical indicators of wine and wine grape monitoring will ref lect the conditions of wine and wine grapes to some extent, and establish models to solve problems. This paper mainly solves the problem by using normal distribution and variance test, establishing principal component analysis, multiple linear regression, cluster analysis, correlation coefficient and stepwise regression model.

　　Keyword：　wine; normal distribution; principal component analysis; multiple linear regression; cluster analysis;

　　确定葡萄酒的质量好坏需要有资质的评酒员对其进行分类指标打分, 最后综合确定葡萄酒的质量。酿酒葡萄的质量直接决定了所酿葡萄酒的质量, 葡萄酒和酿酒葡萄中所检测出的理化指标也在一定程度上反映了葡萄酒和葡萄的质量。

　　1 模型的建立及求解

　　1.1 问题一:判断显着性差异和评价可信度

　　1.1.1 正态分布检验

　　分析品酒员评分的平均值是否符合正态分布, 需要绘制相应的图表。如果正态概率图中期望累计概率和观测累计概率分布近似分布在斜率为1的直线上, 则该数据近似或服从正态分布[1]。经过对图表的分析可知, 两组数据均可看作近似正态分布。

　　1.1.2 参数的显着性差异

　　运用单因素方差分析法[2], 因各组数据个数相等, 称为均衡数据, 所以采用处理均衡数据的用法为:p=anoval (x) 进行处理。第一组与第二组红葡萄酒p=0.117 5>α=0.05, 即第一组, 第二组红葡萄酒的品尝评分无显着差异;白葡萄酒与此类似, 得出第一组与第二组白葡萄酒p=0.022 6<α=0.05, 即第一组, 第二组白葡萄酒的品尝评分有明显差异。

　　1.2 问题二:对酿酒葡萄进行分级

　　1.2.1 多元线性回归方程的建立

　　由主成分分析模型我们得出了5个主成分, 为了利用这5个主成分建立聚类分析模型, 先根据这5个理化指标建立葡萄对葡萄酒质量的多元线性回归模型。利用附录程序三可以得出与F对应的概率P=0.042 5<0.05, 回归模型:

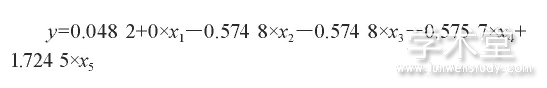
　　(y:葡萄酒质量;x1:氨基酸;x2:蛋白质;x3:花色苷;x4:有机酸;x5:酚类) 成立。

　　1.2.2 聚类分析模型的建立

　　我们把5个主成分经过线性回归可以得到一个较好的回归模型, 所以用这5个主成分的数据进行聚类, 聚类得到树型图, 横轴为红葡萄的样品名, 纵轴代表类间的最长距离。我们可以根据主观判断在中间添加一条横线, 将红葡萄聚类成4类[3] (数字代表样品号) 。

　　第一类:3, 6, 4, 10, 25, 20, 19, 23

　　第二类:2, 9, 14, 5, 13, 26

　　第三类:1, 8, 24

　　第四类:7, 22, 12, 15, 18, 21, 11, 16, 17, 27

　　对每一类分别计算平均得分, 结果如下:

　　红葡萄第一类:71.825等级 (二) ;第二类:72.950等级 (一) :第三类:68.533等级 (四) ;第四类:68.600等级 (三) 。

　　计算每个等级红葡萄各理化指标均值, 结果如表1所示。

　　表1 每个等级红葡萄各理化指标均值

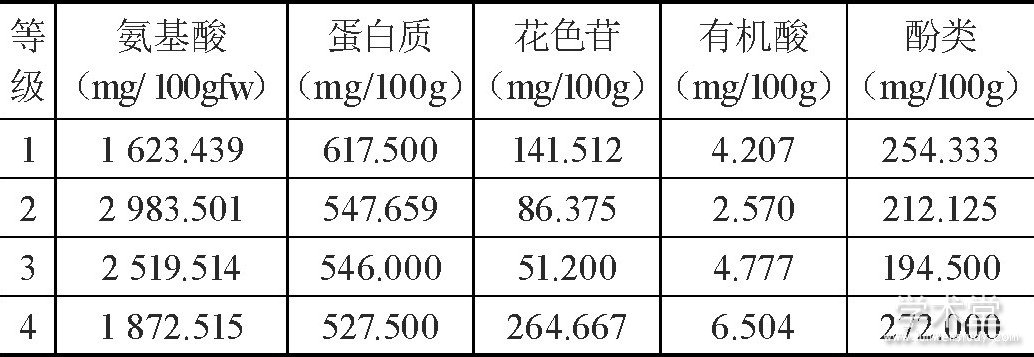
　　等级一优于其他等级的主要原因很可能是因为葡萄的蛋白质的含量远大于其他组。同理, 之后进行线性回归, 可以得出与F对应的概率P=0.034 11<0.05, 回归结果为:

　　(y:白葡萄酒质量;x1:氨基酸;x2:蛋白质;x3:花色苷;x4:有机酸;x5:酚类;x6:醇类;x7:还原糖) 成立。所以, 我们可以利用这7个主成分建立聚类模型, 将白葡萄聚类成4类。

　　第一类:6, 27, 13, 17

　　第二类:4, 8, 16, 9, 19, 7

　　第三类:1, 11, 15, 18, 24, 2, 21

　　第四类:3, 28, 5, 20, 22, 10, 14, 25, 12, 23, 26

　　对每一类分别计算平均得分, 结果如下:

　　白葡萄第一类 (76.675) , 第二类 (74.583) , 第三类 (76.500) , 第四类 (77.564) 。

　　计算每个等级红葡萄各理化指标均值, 等级一优于其他等级的主要原因很可能是因为葡萄的氨基酸和还原糖的含量远大于其他组[4]。

　　1.2.3 求解结果

　　通过最后的数据分析, 假设上述聚类分析是合理的, 可以看出, 品质差的葡萄不能酿出好的葡萄酒, 品质好的葡萄并不一定能酿出质量高的葡萄酒, 可能会涉及许多其他的因素, 如酿造的过程, 工艺水平还有葡萄酒本身的理化指标;可以得出与题设一样的结论, 酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系。

　　1.3 问题三:相关系数模型和逐步回归模型

　　1.3.1 相关系数模型

　　相关系数模型中的相关系数是判断相关程度的指标, 相关系数用r表示, |r|越大, 相关程度越大。相关系数的计算方法如下:

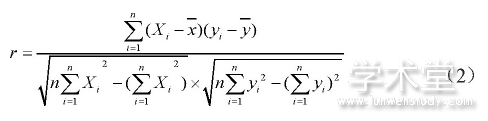
　　相关系数模型针对葡萄和葡萄酒相同的理化指标进行分析, 经汇总发现红葡萄与红葡萄酒有9个相同的理化指标, 白葡萄与白葡萄酒有8个相同的理化指标, 由于每个指标都有不同的权重和性质, 所以首先对各个原始数据进行标准化处理。相关系数如表2所示。

　　由表2可知, 红葡萄酒中, 花色苷、单宁、总酚、酒总黄酮、1, 1-二苯基-2-三硝基苯肼 (1, 1-diphenyl-2-picrylhydrazyl, DPPH) 相关性比较强。同理, 可得到白葡萄酒中, 单宁、总酚、酒总黄酮的相关性比较强。

　　表2 红葡萄酒各指标相关系数

　　1.3.2 逐步回归模型

　　逐步回归过程使用sterwise函数[5]分别对红葡萄酒和白葡萄酒中每一个理化指标与红葡萄和白葡萄的每一个理化指标的相关性进行分析, 根据分析结果, 只有x4, x6是方程中的变量, 其他的都从模型中移去, 所以表达式为:

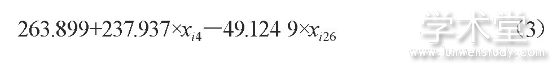
　　1.4 因子分子模型

　　1.4.1 酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响

　　葡萄酒的每个指标都受酿酒葡萄中某些理化指标的影响[6], 例如对于红葡萄酒的花色苷指标受红葡萄的花色苷和出汁率两个指标的综合影响, 函数为:

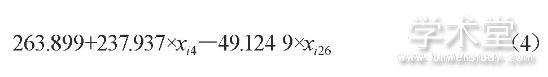
　　1.4.2 酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响

　　筛选出来的理化指标应该与相应的葡萄酒质量存在较大的关联度, 由问题三的解答中可以知道红葡萄酒与花色苷、单宁、总酚、酒总黄酮、DPPH相关性等理化指标相关性较强, 白葡萄酒与单宁、总酚、酒总黄酮的理化指标相关性比较强。

　　2 模型的推广

　　(1) 对于问题一建立的模型不仅适合于解决评分的差异性显着判断, 还可以用于社会科学、行为科学、生物科学和数理科学等领域。

　　(2) 主成分分析模型中的降维技术也可用到多种多影响成分的分析中去, 另外, 聚类模型也可以用于生活中大部分的分级问题。

　　(3) 对于问题三建立的相关系数模型和逐步回归模型, 可以推广到其他领域, 如生物科学、数理科学等, 分析两个变量之间的关系。

　　参考文献：

　　[1]杨希冬.实验数据异常值的剔除方法[J].唐山师范学院学报, 1998 (5) :56-57.
　　[2]刘荣, 冯国生, 丁维岱.SAS统计分析与应用[M].北京:机械工业出版社, 2011.
　　[3]聂继云, 李明强, 张桂芳, 等.白梨品质评价指标的聚类分析[J].中国果树, 2000 (2) :16-17.
　　[4] 百度百科.葡萄酒[EB/OL]. (2010-09-09) [2018-04-08].http://baike.baidu.com/view/23275.htm.
　　[5]谢中华.MATLAB统计分析与应用:40个案例分析[M].北京:北京航空航天大学出版社, 2010.
　　[6]韩中庚.数学建模方法及其应用[M].北京:高等教育出版社, 2009.