摘 要: 针对柔性作业车间调度问题中的约束条件,考虑到低碳排放是制造业急需解决的问题,构建了一种基于最大完成时间和最大能耗的数学模型,提出一种改进的多目标优化算法。首先,在传统的NSGA-Ⅱ算法中融入粒子群算法的思想,提高解集的搜索能力;其次,将机器和工序部分进行分层编码,保证解集的合法性;然后,使用一种改进的密度估计方法计算平均距离,保证解集的分布性。为了验证算法的有效性,使用mk01~mk07标准测试数据对NSGA-Ⅱ算法及改进的多目标优化算法进行对比实验。结果显示,改进后算法得到的Pareto最优解集在解的多样性及收敛性方面优于传统多目标算法。
关键词: 柔性作业车间调度; 多目标优化; 能耗; 分层编码; 调和平均数; 融合非支配排序进化算法;
Abstract: In view of the constraints in the flexible job shop scheduling problem,an urgent issue of low carbon emission to be solved in the manufacturing industry is considered,a mathematical model based on maximum completion time and maximum energy consumption is constructed,and an improved multi-objective optimization algorithm is proposed. The particle swarm optimization is integrated into the traditional NSGA-Ⅱ algorithm in order to improve the search ability of solution set. The parts of machine and process are subjected to hierarchical coding to ensure the validity of the solution set. An improved density estimation method is used to calculate the average distance to ensure the distribution of the solution set. In order to validate the validity of the algorithm,mk01 ~ mk07 standard test data is used to perform contrast experiments to make comparison between the NSGA-Ⅱ algorithm and the improved multi-objective optimization algorithm. The results show that the Pareto optimal solution set obtained by the improved algorithm is superior to that by the traditional multi-objective algorithm in terms of diversity and convergence of solution.
Keyword: flexible job shop scheduling; multi-objective optimization; energy consumption; hierarchical coding; harmonic average; fusion non-dominated sorting genetic algorithm;
0、 引言
近年来,车间调度问题也面临着环境和经济的双重解决问题[1],因此,通过提高资源的利用率来降低能耗的产生对于节能减排这一目标具有极其重要的意义。在当前行业中设计一种降低能耗的模型对于提高生产效率必不可少[2]。
现实生活中,单目标已经无法满足人们对于优化得到最优解的需要,传统的多目标处理方法是将多目标问题通过加权和的方式转变为单目标问题求解,这种方法的优点是操作简易,缺点是每次只能获得一个解,多目标Pareto方法是在求解的过程中同时考虑多个目标,产生一组Pareto最优解,减少了计算时间,增加了解的多样性[3]。
文献[4]对车间调度的标准进行评价,并设计了一种改进的遗传算法来优化工业机器在加工不同工件时产生不同能耗的问题。文献[5]建立了车间调度的完工时间、加工成本、质量以及能耗四个目标的最小化模型,然后提出一种基于广泛数值分析的性能评估方法。文献[6]建立了一种优化能源消耗和使工作流程更灵活有效的调度模型,并对金属加工工厂车间生产调度问题的案例进行了研究。文献[7]以能耗和平均时间为目标,建立了基于遗传算法的车间作业调度问题的多目标研究方法。文献[8]设计了相应的矩阵编码、交叉算子,改进了非劣前沿分级方法,并提出了基于Pareto等级的自适应变异算子以及精英保留策略。

传统的多目标优化算法在求解柔性作业车间调度问题时会出现解集个数和目标函数值并不如意的情况,因此,改进传统的多目标优化算法对于得到更多的解集个数,提高算法的快速收敛性具有重要意义。
1、 问题描述及数学建模
1.1、 多目标优化理论
首先给出有关多目标优化问题的一般描述[9],给定决策向量X=(x1,x2,…,xn),满足下列约束:
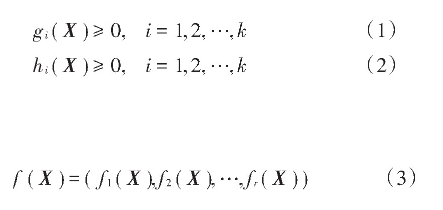
设有r个相互冲突的优化目标,则优化目标可以表示为:
寻求X*=(x1*,x2*,…,x*n),使f(X*)在满足约束条件(1)和(2)时达到最优。
多目标优化中,各个目标的解相互约束,最优解未必只有一个,在进行多目标问题的研究过程中,不能简易地比较各解,通常可求得不比其他任何解差的解集[10],相比于传统的将多目标转为单目标的方法,增加了解的多样性,为决策者提供了一个较佳的选择空间。
1.2、 柔性作业车间调度问题理论
柔性作业车间调度问题(Flexible Job Shop Scheduling Problem,FJSP)是一类进行任务配置和顺序约束的资源分配问题,关于FJSP的描述[11]如下:
n个工件,集合表示为:J={J1,J2,…,Ji,…,Jn},i∈[1,n];
m台机器,集合表示为:M={M1,M2,…,Mj,…,Mm},j∈[1,m]。
每个工件需要经过若干道工序加工才能完成,每个工件的工序的数目可以是不相同的,并且每道工序可以选择在不同的机器上进行加工[12]。首先需要做出如下约束条件[13,14]:
1)工件在不同机器的加工时间是已知的,且每类工件加工工序已经预先确定;
2)在零时刻所有的工件都可以被加工;
3)加工过程中,任一道工序一旦加工开始则不允许中途中断;
4)同一台机器只能在同一时刻加工一道工序;
5)每道工序必须在其前一道工序完成才能进行后续工序。
1.3、 数学建模
1)最小化最大完成时间
最大完成时间是柔性作业车间调度过程中多个工件同时进行加工,所有工件加工结束需要的时间。时间越短,表明实际生产中的效率越高,其数学表达式为:
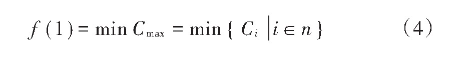
式中:Cmax是指最大完成时间;n表示工件的总数量;Ci表示工件i的完成时间,机器i总的时间等于加工时间runtimei和待机时间idlei的总和。
式(6)表示最小化最大完成时间。
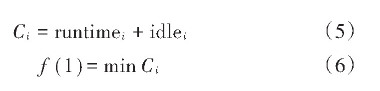
2)最小化最大能耗
机器除了在加工过程中会产生能耗外,在待机时也会产生相应的能耗,随着时间的增加,产生的能耗也会增加,因此,定义关于能耗的数学公式为:
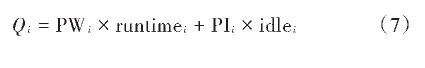
式中:PWi为机器i的加工功率;runtimei为机器i的运行时间;PIi为机器i的待机功率;idlei为机器i的待机时间;Qi为机器i的能耗。
式中:Qi为机器i的加工功率加上待机功率的总和;Q为m台机器的总能耗。
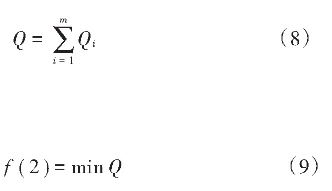
式(9)将最大能耗的目标函数设置为最小值,能耗与完成时间有关,时间越长能耗也就越大。
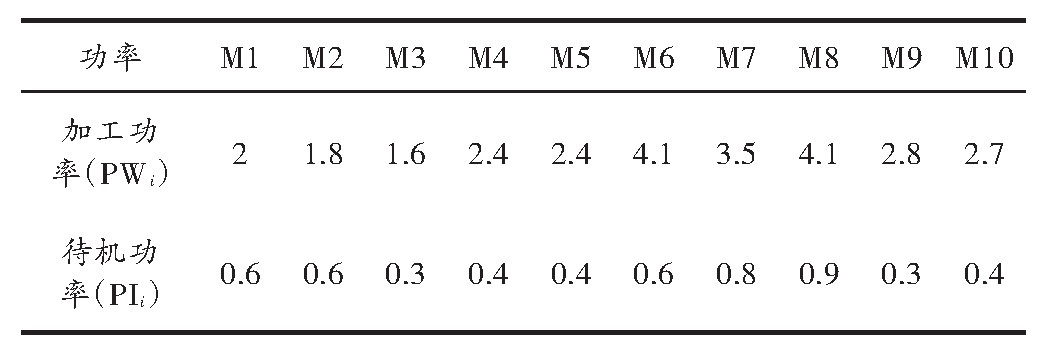
各机器功率参数设置如表1所示。
表1 机器功率表
2 、改进的多目标优化算法流程
NSGA-Ⅱ是目前应用比较广泛的多目标进化算法之一,其在求解多目标问题时应用也比较多,该算法具有运行速度快、解集的收敛性好等优点。改进的多目标优化算法主要是基于融合非支配排序遗传算法(Fusion Non-dominated Sorting Genetic Algorithms,FNSGA)对搜索空间中的个体进行快速非支配排序,算法具体操作流程如下。
2.1、 编解码方式
FJSP需要解决两个子问题,即机器的选择问题和工序的排序问题。为了处理这两个子问题,这里采用分层编码的方式,采用两个L维(L为所有工件的总工序数)向量分别来表示工序和机器,其中,第一行代表工序的排序,向量中的每个分量为不大于工件总数的整数,第二行代表机器的选择顺序,向量中的每个分量为不大于机器总数的整数。
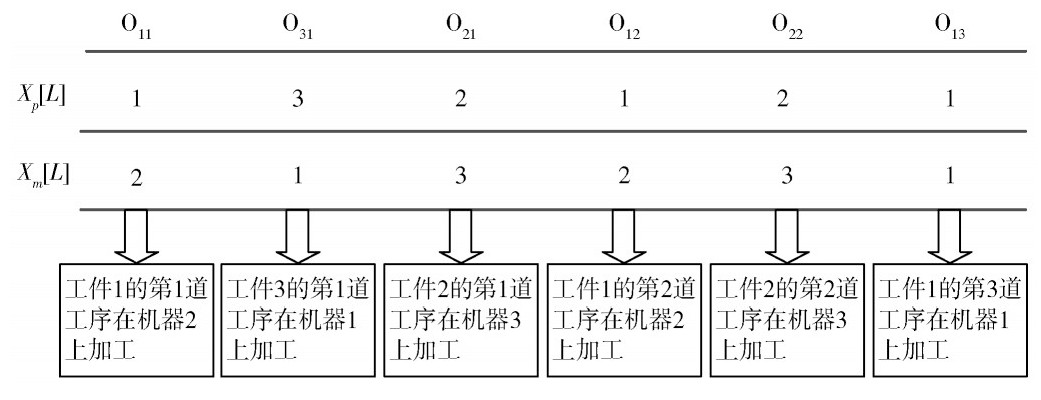
染色体的编码方式如图1所示,这是一个关于3个工件3台机器柔性作业车间调度的问题。第一行是关于工序的排序问题,其中“1”表示工件1,“2”表示工件2;第一行第一次出现的“1”表示工件1的第一道工序,第二次出现的“1”表示工件1的第二道工序;第二行是关于机器的选择问题,其中,第一个元素“2”表示工件1的第一道工序在机器2上加工,第二个元素“1”表示工件3的第一道工序在机器1上加工。
图1 编码方式示意图
解码就是将粒子转换为对应的时间矩阵、能耗矩阵、机器矩阵和对应的机器加工向量,根据以上转换产生相应的调度方案,从而根据调度方案生成对应的调度甘特图。
2.2、 初始化
对算法中涉及到的参数进行初始化设置。根据参数设置生成粒子群初始位置,求解初始粒子群的适应度,对初始粒子群进行非支配排序,初始化局部最优粒子群解集和全局最优粒子,保存全局最优粒子。
2.3、 选择操作
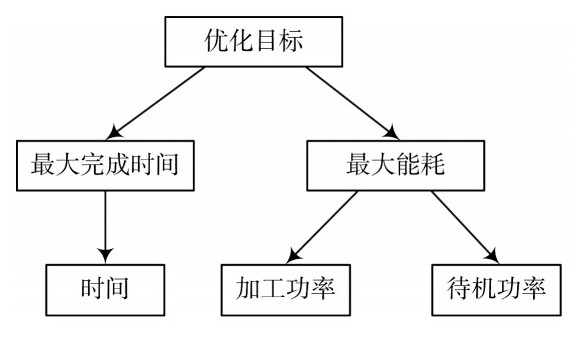
适应度函数的选取对问题的求解非常重要,使用层次分析方法,其思想如图2所示。
具体是重新按工序排好序,根据机器的开始加工时间和结束时间计算机器总的加工时间,这里用到的目标函数为1.3节中的最大完成时间和最大能耗两个目标函数,将对应的粒子xi逐个解码得到机器总的时间向量C,运行时间向量runtime,读取出每个机器的加工功率PWi和待机功率PIi。
图2 层次分析方法图
第一个目标函数最大完工时间为f1(xi)=max(Ci),机器i的空闲时间向量idlei=Ci-runtimei;
第二个目标函数最大能耗为:f2(xi)=max(runtimei?PWi+idlei?PIi)。
粒子xi所对应的适应度函数f(xi)=[f1(xi)f2(xi)],分别计算各目标对应的适应度函数值。
2.4、 交叉操作
选择操作是将具有较高适应度的一半粒子遗传给下一代,同时用适应度好的前一半粒子的位置替代适应度较低的后一半粒子的相应矢量。在交叉操作中,后一半粒子作为待交叉因子,两两进行结合配对,将产生的子代和父代作比较,选择适应度高的一半再进入下一代,更新后代粒子的位置。
按照式(10)和式(11)进行交叉操作,其中,y1,y2是产生的父代粒子;x1,x2是子代粒子;α是与x1维数相同的随机数向量,向量中的每个值α∈(0,1 2)。按照此种方式进行交叉的优点是继承了父代的优良基因。
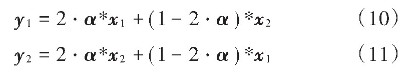
对新产生粒子的位置进行判断,若超过编码范围,则将其重新随机分配在编码范围内,计算交叉后粒子的适应度值。
2.5、 变异操作
对每个粒子产生一个随机数r,r~N(0,1),通过将该随机数和预先设定的变异概率相比较来判断是否进行变异操作。如果变异概率比这个随机数大,则粒子重新进行搜索,其最优位置保持不变,这主要是为了增加遗传算法的全局搜索能力。
结合文献[3]中的变异操作,使用一种停滞阻止策略,通过对全局最优粒子进行变异操作来产生更好的全局最优粒子,减少遗传算法在迭代过程中陷入早熟的现象,防止出现局部最优。
对新产生粒子的位置进行检查,若超出编码范围,则将其重新随机分配在编码范围内,计算变异后粒子的适应度值。
2.6 、多目标优化中拥挤密度估计方法改进
多目标优化算法大多采用密度估计维护进化群体的多样性,为每个个体估计邻域密度值,密度值越大说明个体周围越拥挤,分布性能越差。通过在进化群体中保留邻域密度较小的个体,删除邻域密度较大的个体,保证解集的分布性。
在进行密度估计时,个体密度估计仅考虑周围邻近个体的影响,邻域个体数目为2或k(k<种群数量),使用的距离为欧氏距离,此计算公式的缺点是只考虑了同一Pareto非支配等级个体。
本文采用一种改进的密度估计方法,即Harmonic平均距离(调和平均数),主要用来解决在无法掌握总体单位数的情况下,只有变量值,需要得到平均数的情况下使用的一种数据方法。其思想为:针对种群的第i个个体,假设目标空间中与其距离最近的k个个体的欧氏距离为di,1,di,2,…,di,k,则个体i的Harmonic平均距离di如式(12)所示:
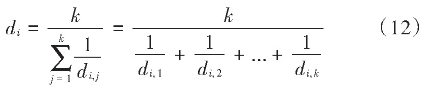
为了避免邻域个体数目和Pareto非支配等级的局限,式(12)中的参数i的取值范围为种群数目为-1,即排除自身个体的影响。
3 、实验结果及分析
mk01~mk07是7组包含不同工件数、不同机器数、不同工序数的部分柔性作业车间调度问题测试数据[15],通过实验得到的Pareto解集个数也不尽相同。FNSGA在各个测试集上进行实验得到的结果如表2所示。表2中,Pareto解集这一列中数据(50,383.5),前者表示最大完成时间为50,后者表示最大能耗为383.5,依次类推。
以下以mk06测试数据为例进行分析,mk06是一组包含10个工件,10台机器,150道工序的柔性作业车间调度问题。
将FNSGA与NSGA-Ⅱ进行单独实验,得到的对比结果见表3。NSGA-Ⅱ得到的第一组数据(3,60,387),3表示Pareto解集个数,60表示最大完成时间最大值,387表示最大能耗最大值,依次类推。结果表明,改进后的算法最大完成时间和最大能耗比改进前少,得到的Pareto解集个数多于或等于未改进前的。算法独立运行30次,最优运行时间对比如表4所示,表中比较了传统的NSGA-Ⅱ只使用GA,PSO以及改进算法的最优运行时间。
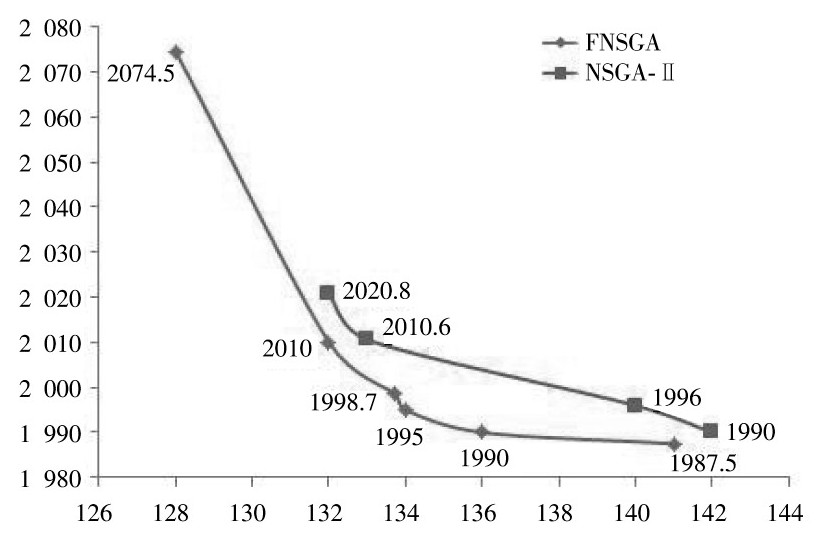
FNSGA和NSGA-Ⅱ算法使用mk06测试数据进行实验得到的Pareto解集的对比实验图如图3所示。图3中,FNSGA得到的Pareto解集共有6个,NSGA-Ⅱ得到的Pareto解集共4个。通过对比观察可以看出,改进后的算法解集个数多于未改进的,同时最大能耗也比未改进的要低,收敛性也较好。
表2 FNSGA Pareto解集表
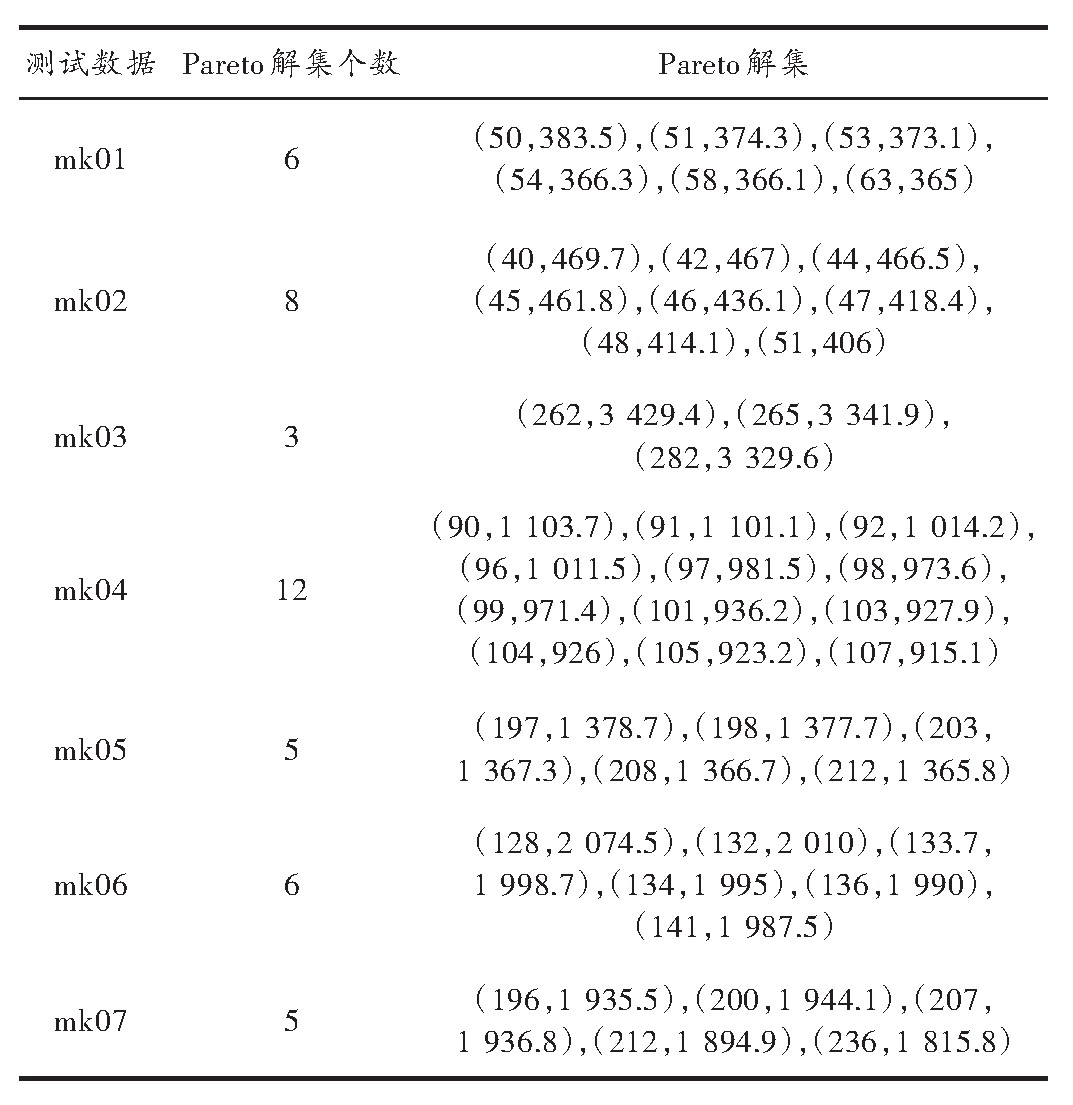
表3 FNSGA与NSGA-Ⅱ算法最大完成时间和最大能耗对比表
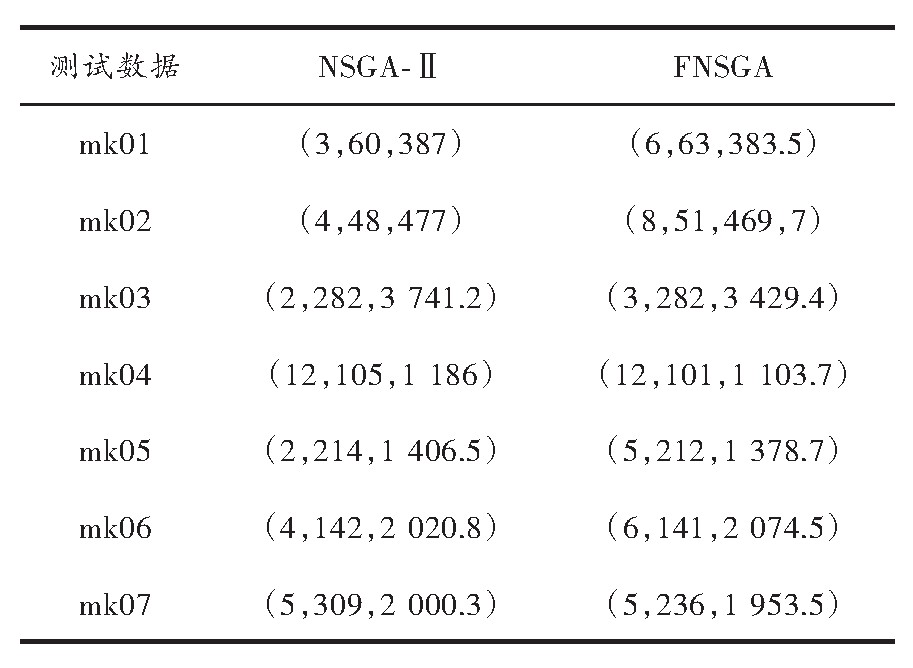
表4 算法独立运行30次最优运行时间对比表
图3 NSGA-Ⅱ与FNSGA非支配解比较图
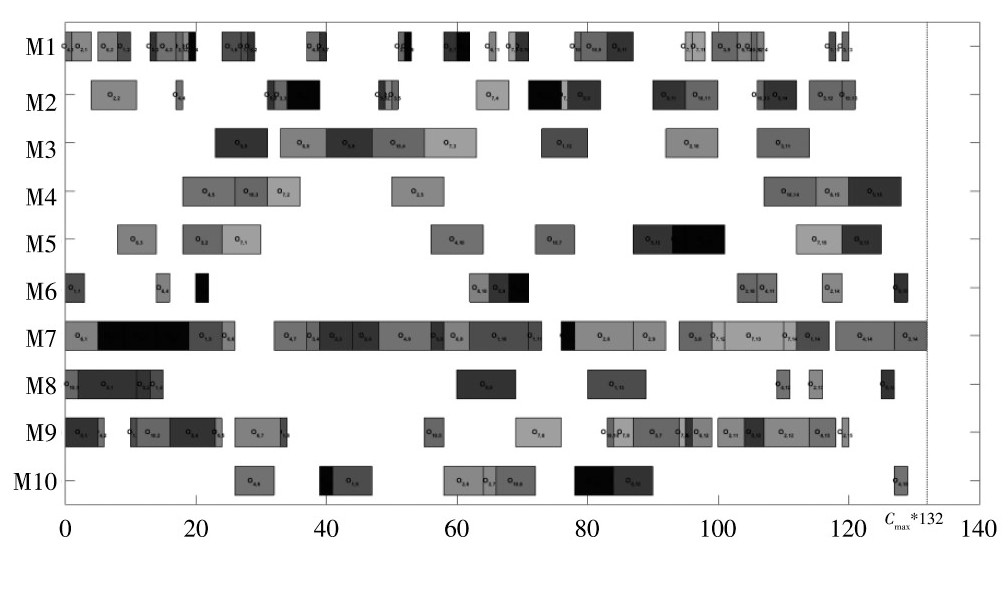
不同的非支配解对应不同的调度方案,因此,得到的最佳调度甘特图也是不相同的。FNSGA算法使用mk06测试数据进行实验,得到的其中一个最佳调度方案如图4所示,图中横坐标表示完成时间,纵坐标表示10台机器,从图4中可以看出不同工序在不同机器上的加工情况,同一颜色代表同一工件,O1,1表示工件1的第一道工序,依次类推。图中Cmax为最大完成时间,最大完成时间为132。
图4 FNSGA算法最佳调度方案图
4、 结语
本文针对柔性作业车间调度和多目标优化的特点,建立了基于考虑最大完成时间和最大能耗的数学模型,通过最小化最大完成时间和最小化最大能耗,在多种约束条件下,使用多目标优化算法,将改进后的算法应用于柔性作业车间调度中,通过在Matlab平台上进行仿真实验,得到最优调度方案和Pareto解集,为决策者的决策提供了多种选择,通过对比实验验证了改进后算法的有效性。
注:本文通讯作者为王鲁。
参考文献
[1]费凡.面向节能优化的多目标柔性作业车间生产调度方法研究[D].合肥:合肥工业大学,2018.
[2]党世杰.低碳排放约束的柔性作业车间调度研究[D].郑州:郑州航空工业管理学院,2017.
[3]吴定会,孔飞,田娜,等.教与同伴学习粒子群算法求解多目标柔性作业车间调度问题[J].计算机应用,2015,35(6):1617-1622.
[4]ESCAMILLA J,SALIDO M A,GIRET A,et al. A metaheuristic technique for energy-efficiency in job-shop scheduling[J].Knowledge engineering review,2016,31(5):475-485.
[5]JIANG Z,ZUO L,MINGCHENG E. Study on multi-objective flexible job-shop scheduling problem considering energy consumption[J]. Journal of industrial engineering and management,2014,7(3),589-604.
[6]DAI M,TANG D,GIRET A,et al. Energy-efficient scheduling for a flexible flow shop using an improved genetic-simulated annealing algorithm[J]. Robotics and computer-integrated manufacturing,2013,29(5):418-429.
[7]MAY G,STAHL B,TAISCH M,et al. Multi-objective genetic algorithm for energy-efficient job shop scheduling[J]. International journal of production research,2015,53(23):1-19.
[8]鞠录岩,杨建军,张建兵,等.改进NSGA算法求解多目标柔性车间作业调度问题[J].计算机工程与应用,2019,55(13):260
[9]-王26淑5.娟.柔性作业车间的多目标动态稳健调度研究[D].济南:山东大学,2014.
[10]梁艳.基于混合型进化算法的柔性制造优化研究[D].大连:大连理工大学,2013.
[11]杨立熙,王秀萍.基于免疫遗传算法求解多目标柔性作业调度问题[J].武汉理工大学学报(信息与管理工程版),2018,40(1):69-74.
[12]毕孝儒,张黎黎,贺拴,等.面向无等待多目标柔性车间调度问题的遗传蜂群优化算法[J].现代计算机(专业版),2015(23):11-16.
[13]王春,张明,纪志成,等.基于遗传算法的多目标动态柔性作业车间调度[J].系统仿真学报,2017,29(8):1647-1657.
[14]KONAK A,COIT D W,SMITH A E. Multi-objective optimization using genetic algorithms:a tutorial[J]. Reliability engineering&system safety,2006,91(9):992-1007.
[15]BRANDIMARTE P. Routing and scheduling in a flexible job shop by tabu search[J]. Annals of operations research,1993,41(3):157-183.