
声学CT温度场测量技术根据多路径声波传播时间数据,推算被测区域的温度分布,属于“由效果反求原因”的逆问题研究,具有非接触不干扰被测温度场、测温范围广和测量对象空间范围大等优点.声学高温计是该技术在工业炉温度场监测中的典型应用,而应用该技术监测深海热液口温度分布和仓储粮食温度分布,则是近几年开始的新的应用研究.目前,国内外声学CT温度场测量技术的研究普遍针对二维层面进行,但在某些场合,如仓储粮食温度分布监测则需要进行三维温度场重建.
为了测量一个三维空间(或二维层面)的温度分布,需将该空间(或层面)划分成若干个三维(或二维)小区域,或称像素,每个小区域重建出一个温度,相当于一个温度采样点.最小二乘法是目前声学CT温度场测量时广泛采用的一种重建算法.该算法要求被测区域划分的小区域数小于声波路径数,因此,重建出的温度点非常少,且边缘像素中心点所界定的区域比传感器所界定的区域小许多.采用适当的内插和外推运算,可获得被测区域细致的温度描述.目前普遍采用的是三次样条插值法,但三次样条法的内插精度虽较高,但外推精度通常很低.
克里金法(Kriging)是20世纪中后期以来应用最广泛的地理空间插值方法.与传统的插值技术相比,Kriging模型有以下优点:1)Kriging模型以己知信息的动态构造为基础,使用估计点附近的某些信息,插值所需条件较少;2)Kriging模型同时具有局部和全局的统计特性,可以分析已知信息的趋势和动态,能够进行外推插值;3)Kriging法作为线性回归分析的一种改进技术,包含了线性回归部分和非参数部分,其中,非参数部分被视作随机过程的实现,可以使插值具有较高的精度和保真度.
为了提高三维温度场声学CT重建精度,本文研究了基于最小二乘法和克里金插值的三维温度场重建,即先用最小二乘法实现被测三维区域的少量像素重建,然后用克里金法对所获得的温度场进行内插和外推运算,从而得到整个被测区域的细致的温度描述.
1、声学CT温度场重建原理
声波在气体介质中的传播速度是气体温度的第一函数.气体介质中的声速c、气体介质的绝对温度T和由气体组成成分决定的声音常数z之间的关系可表示为

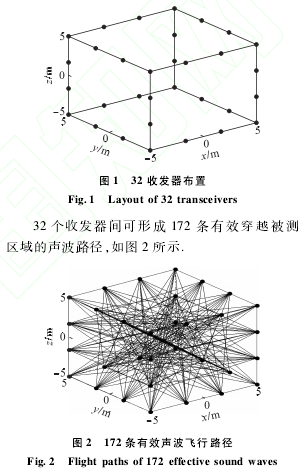
声学CT法测量温度场需要在被测区域周围尽可能均匀地设置多个声波收发器.任一声波收发器发射的声波信号,可被所有的声波收发器所接收,这样就形成穿过被测区域的多条有效声波传播路径.用互相关等时延估计法测量出声波在各有效声波路径上的传播时间,采用适当的重建算法,可由这些声波传播时间及已知的声波收发器位置重建出被测区域的声速分布,进而利用声速与温度的关系,重建出被测区域的温度分布.
2、最小二乘法温度场重建原理
声波从发射器到接收器的传播时间可表示为

式中:a为声速的倒数;ds为声音传播路径的微分.
将被测区域划分成n个小区域,假设声速在各小区域内是均匀分布的,并用ai表示第i个小区域的声速的倒数,用ΔSik表示第k(k=1,2,…,m,m为声波路径总数)条声波路径穿过第i个小区域的长度,则声波在第k条路径的传播时间可表示为
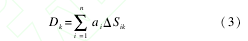
如果用Pk表示声波在第k条路径上传播时间的测量值,那么Dk和Pk之间的误差为
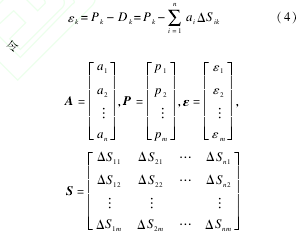
则式(4)可表示为P-SA=ε(5)当传感器放置的位置及测量区域分割的方法确定后,即可求得重建矩阵S.式(5)的最小二乘解为^A=(STS)-1STP(6)这样便可为每个小区域求出一个声速的倒数,再利用声速与温度的关系求出对应的温度值.
3、Kriging模型
Kriging模型是一种基于统计理论的插值技术.通常Kriging模型变量x=[x1,x2,…,xw]与真实响应y之间的关系可表示为y=λf(x)+μ(x)(7)式中:f(x)为回归函数(一般采用多项式形式);λ为回归系数;μ(x)为均值为0、方差为σ2的随机函数.μ(x)的协方差矩阵为cov[μ(x(i)),μ(x(j))]=σ2W[R(x(i),x(j))](8)式中:i,j=1,2,…,ns,ns为采样点数;W为沿对角线对称的相关矩阵;R(x(i),x(j))为采样点x(i)与x(j)的相关函数.相关函数常用平稳高斯函数表示,即

式中,^σ2和W为参数θd的函数.任意一个θd的值都能生成一个插值模型,最终的Kriging模型是通过求解式(13)的无约束非线性最优问题得到的.利用Matlab中Kriging插值工具箱的dacefit和predictor函数,可实现Kriging插值运算.函数dacefit根据试验数据点建立Kriging模型,而函数predictor根据Kriging模型计算待测点的响应值.
构建Kriging模型时要提供回归模型和相关函数句柄.Kriging模型工具箱提供了3种回归模型和6种相关函数.回归模型有常数模型regpoly0、一次多项式模型regpoly1和二次多项式模型regpoly2;相关函数有指数函数、通用指数函数、gauss函数、线性函数、spherical函数和三次样条函数.构建Kriging模型时还要给定相关函数参数向量θ的初值theta0,通常其长度等于维数.但是如果所解决问题为各向同性问题,也可以取为标量,这样优化就会减小.theta0需要用户给定,其取值会影响到模型的精确度,一般要经过多次运算才能确定一个合适的值.本文取回归模型为regpoly1,相关函数为gauss函数,theta0=04.
4、三维温度场重建
假设被测的三维空间为10m×10m×10m的正方体区域,32个声波收发器放置在正方体的每个顶点以及每条棱边的三等分间隔处,布置如图1所示
.
将被测空间划分为4×4×4=64个像素后,可计算出重建矩阵S.利用测量或计算机仿真的方法可获得声波在这些路径上的传播时间,用这些传播时间和最小二乘法,可为每个像素重建出一个温度值,并将该温度值赋予各像素的中心点.仅用64个像素是无法细致地描绘出一个复杂的温度场分布的,本文采用克里金插值法来获得温度场中更多位置的温度值.为了评价本文所提方法的有效性,对式(14)、(15)所描述的单峰和双峰模型温度场进行了仿真重建,并采用最大绝对误差Emax、平均温度的相对误差Eave和均方根误差Erms来评价温度场的重建精度.
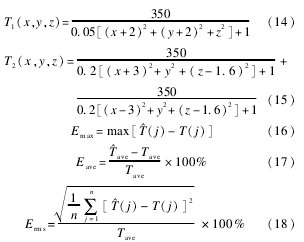
式中:n为被测区域所划分的像素的总数;T(j)和^T(j)分别为模型温度场和重建温度场第j个像素中心点的温度;Tave和^Tave分别为模型温度场和重建温度场的平均温度.
表1给出了最小二乘法获得的4×4×4=64个像素描述的温度场重建误差,该温度场的描述范围为75m×75m×75m.由表1可以看出,双峰模型的重建误差明显比单峰模型的大,这主要是由于双峰温度场分布远比单峰温度场复杂.
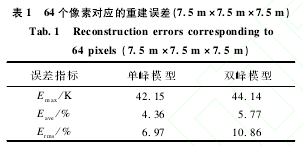
目前普遍采用三次样条法来获得更细致的温度场描述,因此,本文同时提供克里金法和三次样条法对最小二乘法重建结果进行细化描述.表2给出了用克里金法和三次样条法内插获得的20×20×20=8000个像素描述的温度场重建误差.该温度场的描述范围为75m×75m×75m.
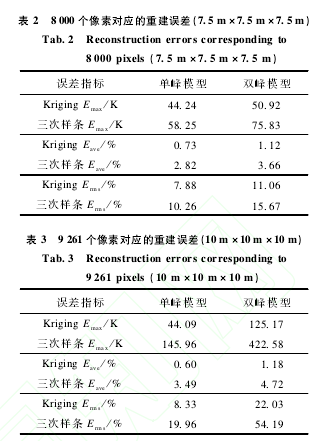
表3给出了用克里金法和三次样条法通过内插和外推获得的21×21×21=9261个像素描述的温度场重建误差.该温度场的描述范围已扩展至10m×10m×10m.图3给出了9261个像素描述的模型温度场以及克里金法和三次样条法细致化后的重建温度场.
由表2、3和图3可以看出:1)三次样条法虽具有较高的内插精度,但其精度明显低于克里金法所获得的精度;2)当涉及到外推运算时,三次样条法的外推数据误差非常大,外推数据不具有实用价值,而克里金法的外推数据仍有较高的精度,最小二乘法与克里金法相结合,可获得10m×10m×10m范围内温度场的细致描述.
5、结论
本文提出的最小二乘法和克里金插值相结合的重建方法,可有效克服最小二乘法重建出的温度点非常少,且边缘像素中心点界定区域比传感器界定区域小许多给被测温度场细致描述带来的严重障碍.将最小二乘法和克里金插值相结合,可实现三维温度场的更高精度声学CT重建.