疼痛暴露对新生儿心率变异性指标的影响

　　
　　1 引 言。
　　
　　新生儿， 尤其是新生儿重症监护室 （NICU） 中的新生儿需要经受日常的， 但带有疼痛的检查诊断 [1]. 在这些过程中， 通常没有采取缓解疼痛的措施。 目前有足够的证据认为， 新生儿 （包括早产新生儿） 有疼痛感觉。 新生儿对包括疼痛在内的一系列急性应激可产生内分泌、免疫、自主神经和行为改变为特征的适应性反应。 受到反复疼痛刺激的新生儿， 其应激调控系统会发生改变， 导致神经系统结构和功能重组， 并严重影响脑的发育[1,2].
　　
　　大多数新生儿的疼痛刺激没有得到合适的干预， 而准确的疼痛评估是进行疼痛干预的必要条件。 由于新生儿无法自述疼痛， 所以只有采取其他替代方法来评估疼痛。 通常通过观察新生儿的行为或其生理指标来评估其疼痛状态。 与疼痛相关的行为包括面部表情的改变、身体的移动和哭闹的变化； 与疼痛相关的生理指标包括心率、呼吸频域、血压和血氧饱和度。 然而， 以这些指标为基础的疼痛评估存在以下缺陷[3]: 1）即使由训练良好的护士实施， 其可信度仍然存在疑问， 特别是在区分疼痛和不舒适时； 2） 一些疼痛量表需要进行长时间的医学观察； 3） 对疼痛进行的评估是间歇性的， 在评估间期发生的疼痛可能会被疏漏。
　　
　　通过心拍间期之间的波动反映出来的心率变异性（heart rate variability, HRV）是评价自主神经系统功能的最有价值的非侵入式方法， HRV 分析在麻醉深度监测[4]、心衰诊断 [5] 和精神疲劳评估 [6]等方面应用广泛。 疼痛的反应包括自主神经系统的反应。 许多报告指出， 新生儿经受足跟取血诱发的疼痛时， 自主神经系统功能有着显着改变， 并通过 HRV 的相关指标反映出来。 现有报告大多使用时域或频域等线性方法分析新生儿疼痛暴露时心率变异性的变化， 忽视了心率变异性中的非线性机制。 就作者所知， 目前仅文献 [7] 采用 Poincaré 散点图、去趋势波动分析、近似熵和样本熵等非线性方法研究了新生儿疼痛暴露过程中相应的非线性机制。
　　
　　新生儿出生 2-5 天内， 通常需要进行足跟取血， 用以筛查苯丙酮尿症和甲状腺功能减低症。 本文研究了足跟取血时针刺诱发的疼痛对新生儿自主神经系统的影响， 全面分析了疼痛暴露对新生儿心率变异性时域指标、频域指标和非线性指标的影响。 本文采用的非线性方法有 Poincaré 散点图、去趋势波动分析、递归图分析、近似熵、样本熵和关联维等。 在上述研究的基础上， 将得到的所有HRV指标组成特征空间， 采用支持向量机 （support vectormachine, SVM） 方法建立了若干可用于新生儿疼痛检测的模型。
　　
　　2 研究对象与方法。
　　
　　2.1 研究对象。
　　
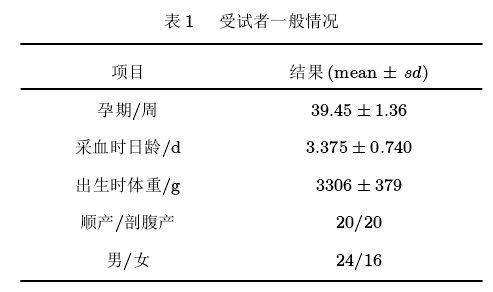
　　选择 40 名因疾病筛查在湖南某医院进行足跟采血的健康新生儿为研究对象 （见表1）。 新生儿母亲无吸毒史， 胎龄 36-42 周， 顺产或剖腹产， 新生儿出生体重 2400-4100 g, 5 min Apgar 评分大于或等于 9 分。 采血时间为出生后 2-5 d, 采血均在上午9 : 00-11 : 30进行， 采血一次性成功。本研究方案经当地医学伦理委员会批准， 新生儿父母或其监护人均口头同意参与该研究。
　　

　　
　　2.2 心电信号的采集。
　　
　　采用深圳迪美泰数字医学技术有限公司生产的微型心电记录仪 （产品型号： Di Care-m1CP） 记录心电数据， 采样频率设置为 400 s/s. 新生儿的足跟采血在一个安静的房间中进行。 除了医护人员外， 每次仅有一名新生儿及其监护人进入该房间。 新生儿以仰卧方式放置于病床上， 粘贴电极片，接上导联线后休息 5 min, 然后开始采集心电数据。
　　
　　采集的心电数据超过 3 min 时间长度后， 实施足跟取血， 持续记录心电数据， 直到足跟针刺后 3 min（见图1,2）。 足跟采血和心电采集由不同的高年资护士实施。 采用 II 导记录心电数据， 采集到的心电数据保存在心电记录仪的 TF 卡中。 记录完成后，取出TF卡， 通过读卡器输入个人电脑保存。
　　
　　2.3 HRV分析方法与指标。
　　
　　HRV 分析方法分为线性分析 （见表2） 和非线性分析 （见表3） 两大类。 其中线性分析包括时域分析和频域分析。 时域分析的相关指标直接从 RR间期序列中计算得到。 为得到频域分析的指标， 首先通过 Welch 周期图法计算功率谱密度 （见图3），LF 为低频段 （0.04-0.15 Hz） 功率， HF 为高频段（0.15-0.4 Hz） 功率， 两者之比即为 LF/HF. 非线性分析方法包括Poincaré 散点图[8]、去趋势波动分析（detrended ?uctuation analysis, DFA）[9,10]、递归图分析（recurrence plot analysis, RPA）[11,12], 以及近似熵（approximate entropy, Ap En）[13,14]、样本熵（sample entropy, Samp En）[15]和关联维 （correla-tion dimension）[15,16].Poincaré 散点图是 HRV 分析中一种常用的非线性分析方法， 表示连续 RR 间期的相关程度。 为了得到Poincaré 散点图中的参数， 首先需要图示出RRi+1作为RRi的函数， 一般采用一个长轴或短轴位于直线RRi+1= RRi上的椭圆拟合图中的散点， 图中散点垂直于RRi+1= RRi方向的标准差用SD1表示， 图中散点平行于RRi+1= RRi方向的标准差用SD2表示（见图4）。DFA 分析度量信号内部的相关程度。 进行DFA分析， 首先需对RR间期序列进行积分

　　
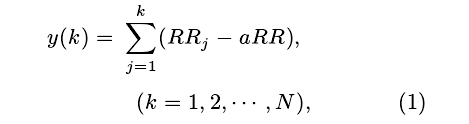
　　其中，a RR为平均 RR 间期长度，N为 RR 间期个数。y（k）被分成长度均为n, 且无重叠的若干段， 在每段内部采用最小二乘法对数据进行拟合， 拟合得到的数据用yn（k）表示。 然后计算

　　
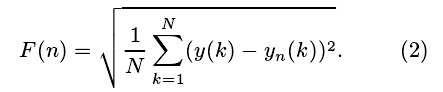
　　取n = 4, 5,· · ·, 16, 得 到 一 组 数 据 （logn,log（F （n）））, 采用最小二乘法对这组数据进行拟合，其斜率即 DFA 分析的短期波动斜率α1. 相应地，取n = 16, 17,· · ·, 64时， 得到 DFA 分析的长期波动斜率α2（见图5）。
　　
　　递归图分析是度量时间序列复杂度的另一种方法， 要绘制递归图， 首先需要计算向量

　　
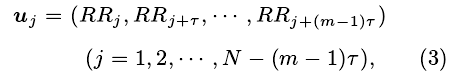
　　其中，m称为嵌入维，τ为延迟时间。 递归图是一个大小为[N-（m-1）τ]×[N-（m-1）τ]的对称矩阵， 取值为 0 或1. 计算递归图中第j行第k列元素的方法如下：
　　

　　
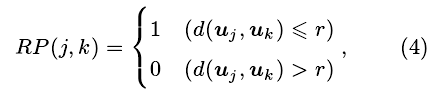
　　其中，d（uj, uk）为向量uj与uk的欧氏距离， 计算如下：
　　

　　
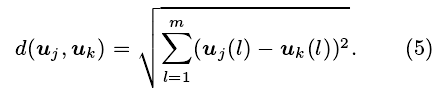
　　取m = 10,τ = 1,r = SD,SD为 RR 间期序列的标准差。 递归图分析中的参数递归率 （REC） 计算如下：
　　

　　
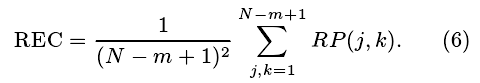
　　递归图分析中另一个参数Lmax为平行于递归矩阵主对角线的线段中， 所有点的取值之和的最大值。另外， 取Lmin= 2, 则参数Lmean计算如下：
　　

　　
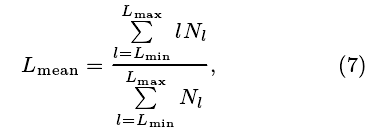
　　其中，l为平行于主对角线的线段取值之和，Nl为平行于主对角线的线段中， 取值之和为l的线段数量，Lmean称为平均对角线长度。 确定性 （DET） 计算如下：
　　

　　
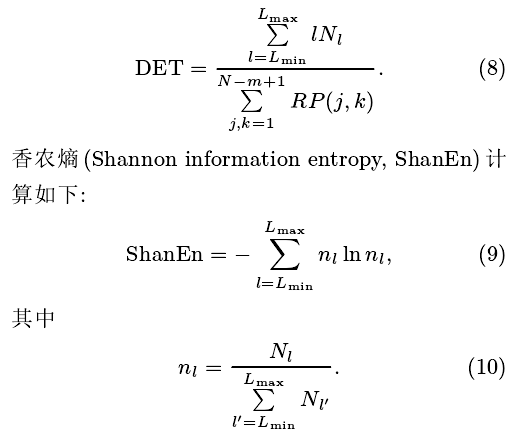
　　近似熵是测量信号复杂度或不规则度的指标，取值越大， 复杂度或不规则度越大。 计算近似熵，首先需要计算向量

　　
　　样本熵的计算与近似熵类似， 首先需要根据（11） 式计算向量uj, 并根据 （12） 式定义距离， 然后根据以下公式计算样本熵：
　　

　　
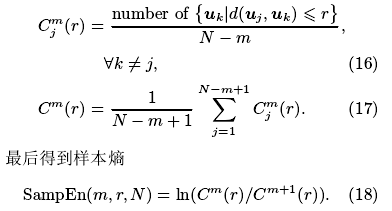
　　关联维同样是计算RR间期序列复杂度的一种方法， 与近似熵类似， 计算关联维D2首先要根据（11）式计算向量uj, 然后定义距离

　　
　　实际计算时， 取（logr,logCm（r））线性拟合的斜率为近似的关联维D2.
　　
　　2.4 实验数据与统计方法。
　　
　　实验数据分为疼痛前组和疼痛组。 疼痛前组和疼痛组的心电数据分别来源于针刺足跟前后的3 min 时间内。 在 3 min 时间里， 选择一段长度为2 min 的较为清晰的心电数据进行HRV分析。 比较疼痛前后的 HRV 时域、频域和非线性指标。 采用Wilcoxon 符号秩检验进行统计分析， 若p值小于0.01, 认为两组数据具有统计学差异。
　　
　　2.5 分类方法及性能评价

    选择径向基核函数的 SVM 方法 [17]建立疼痛检测模型。 使用 libsvm3.17工具包 [18], 首先将数据归一化， 采用网格搜索确定支持向量机的罚函数系数c和属性系数g.
　　
　　10 重交叉验证方法验证分类器性能。 四个常用指标[19]: 正确率、灵敏度、阳性预测率、阴性预测率评估分类器的性能（见表4）。 被分为 “疼痛”组的样本称为阳性。 在表4中， TP表示被正确分类的疼痛组样本数目， TN 表示被正确分类的疼痛前组样本数目， FN 表示疼痛组样本被错误分类到疼痛前组的数目， FP 表示疼痛前组样本被错误分类到疼痛组的数目。
　　
　　2.6 特征选择

    尽管可以采用表2和表3所列的全部 HRV 线性指标和非线性指标训练分类器， 但由于指标过多， 并且指标之间不是相互独立的， 可能导致分类器出现过拟合现象， 造成分类性能下降。 本文对所有2, 3, 4, 5 个指标的可能组合均采用 SVM分类器进行了分类， 并将分类正确率最高的两组指标组合列出。
　　
　　3 结 果。
　　
　　3.1 针刺前后HRV分析。
　　
　　图1为新生儿针刺后的心电信号， 在这段 10 s的时间里， 平均心率为 144 次/min. 图2示出了一段新生儿针刺前后各 3 min 的连续 HRV 时间序列，在该图中， 针刺后 RR 间期减小， 心率加快。 图3为针刺前后的功率谱密度， 高频（低频）段的曲线下面积即为 HRV 的频域参数 HF（LF）。 图4为针刺前后的Poincaré 散 点 图， 该图中的散点反映了相邻RR间期之间的相互关系， 图中拟合椭圆的短轴和长轴长度即为 SD1 和SD2. 图5为 DFA 分析示意图， 将（2） 式中n与F（n）的关系用双对数坐标给出， 即得到图中各点， 用最小二乘法拟合各点， 所得直线的斜率即为α1和α2. 图6为关联维分析示意图， 将（20） 式中Cm（r）与r的关系用双对数坐标给出， 即得到图中各点， 对各点线性拟合得到的直线斜率即为D2.
　　
　　3.2 疼痛前组与疼痛组HRV指标的统计分析。
　　
　　疼痛前组与疼痛组线性指标的统计分析结果如表5所示， 非线性指标的统计分析结果如表6所示。
　　
　　3.3 新生儿疼痛检测模型

    对疼痛前组和疼痛组的样本进行 HRV 线性和非线性分析， 得到相应的指标， 将所有指标组成特征空间， 通过穷举法对所有 2, 3, 4, 5 个指标的可能组合采用 SVM 建立疼痛检测模型， 并将检测正确率最高的两组指标组合列于表7, 表7同时列出了SVM检测模型的相关参数。
　　
　　4 讨 论。
　　
　　本文研究比较了健康足月新生儿在足跟取血导致的疼痛暴露前后的心率变异性线性和非线性指标的变化。
　　
　　从表5可知， 疼痛暴露导致新生儿心率变异性指标 a RR 显着减小， LF 和HF 显着降低， 表明疼痛导致新生儿心率加快， 副交感神经活动降低。 本文的结果与文献 [7, 20] 一致。 从表5可知， 其他线性指标， 如 SDNN 和 RMSSD 的均值在疼痛暴露中出现下降， 但没有显着性差异， 而文献[7]的研究表明，这两个指标显着下降， 具有统计学差异， 考虑到文献 [7] 的样本容量仅为 24, 而本文的样本容量为 40,本文的结果更有说服力。 对于反映交感 -副交感平衡的指标 LF/HF, 其均值在疼痛暴露中出现上升，但无统计学差异， 与文献[20]的报道一致。
　　
　　线性分析需要假设 RR 间期序列具有线性特性， 而这一假设并不成立。 非线性分析无须假设RR 间期序列具有线性特性， 因而能够量化心率控制机制中的非线性因素。 尽管许多研究 [21]指出了非线性分析在心率变异性研究中的重要意义， 然而， 就作者所知， 目前仅有一篇文献报告了新生儿疼痛暴露时部分心率变异性非线性指标的变化情况。 文献[7]的研究表明， 疼痛暴露导致Poincaré 散点图中 SD1 和 SD2 显着下降。 本研究表明， 与疼痛前组相比， 疼痛组的 SD1 和 SD2 的均值出现下降，但没有统计学差异。 文献 [7] 所述新生儿疼痛前的Poincaré 散点图呈扇形， 而疼痛时散点图不再具有扇形分布的现象在本研究中亦有发现 （见图4）， 但不具有普遍性。 DFA 分析能够定量分析 RR 间期序列的相关性和自相似性。 白噪声的α指数值为0.5, 分形信号的α指数值约为 1, 而具有强相关性的布朗噪声的α指数值为1.5[22]. 从表 6可知， 疼痛前组的短期α指数值α1均值为1.32, 而疼痛暴露导致该值降为 1.23, 且具有统计学差异， 表明新生儿的RR间期序列在短期尺度上具有较强的相关性和自相似性， 而疼痛暴露导致其短期相关性和自相似性降低。 与之相反， 在长期尺度上， 疼痛前组α2均值为 1.15, 而疼痛组α2均值上升到 1.30, 且具有统计学差异， 表明疼痛暴露导致新生儿 RR 间期序列长期尺度上的相似性和自相关程度上升。 本研究的结果与文献 [7] 的结果基本一致。 新生儿疼痛暴露导致另外三个非线性指标近似熵 Ap En、样本熵 Samp En 和关联维D2出现下降， 其中， Ap En 和Samp En 的下降具有统计学差异。 近似熵和样本熵的下降在文献 [7] 中已有报告， 本研究的实验结果支持了该文献的报告， 而就作者所知， 本文首次报道了疼痛暴露过程中关联维D2的变化情况。 这三个反映复杂度指标的下降， 表明疼痛暴露导致心率的调控方式更接近周期性， 同时反映出心脏起搏点的调节能力和适应能力受到削弱。
　　
　　疼痛暴露过程中的上述线性指标和非线性指标的变化趋势， 与成年人情绪紧张 [23]时的情况类似， 也与某些疾病如心衰对成年人造成的影响类似， 因而可以从自主神经调控机制的角度认为， 疼痛暴露对健康新生儿造成了负面影响。
　　
　　本文采用 RPA 分析研究了疼痛暴露过程中相关指标的变化。 从表6可知， 疼痛暴露导致 RPA分析的 5 个非线性指标Lmean,Lmax, REC, DET,Shan En 均显着上升。 RPA 分析在心率变异性分析领域的研究尚不深入， 在新生儿疼痛暴露的研究中没有可以比较的文献， 本文的研究初步表明， RPA方法能够较好地反映新生儿疼痛过程中自主神经系统的调控情况， 但其背后的生理学机制有待深入研究。
　　
　　在所有线性指标中， 仅有 a RR、LF 和 HF 三个指标在疼痛前后具有统计学差异， 而在非线性指标中， 有 9 个指标具有统计学差异。 另外， SVM 建立疼痛检测模型时， 在由穷举法得到的特征组合中，非线性指标的数目多于线性指标。 从而表明， 与线性指标相比， 非线性指标能更好地反映疼痛暴露过程中新生儿的心率变异性特征的变化。
　　
　　从表7可知， 基于两个 HRV 指标和 SVM 的疼痛检测模型， 检测正确率可达到 78.75%, 而基于 5 个 HRV 指标和 SVM 的模型， 正确率可达到83.75%, 表明建立的疼痛检测模型具有临床应用的前景。
　　
　　需要提到的是， 尽管在特征选择时， 有主成分分析（principal component analysis）等方法可用于特征空间的降维， 但这些方法无法从理论上证明可以得到适合分类器的特征组合。 本文通过穷举法得到特征组合， 为建立新生儿疼痛检测模型提供了准确的解决方法， 但也导致了特征选择过程中计算量的大量增加。

 

　　参考文献：

　　[1] Weissman A, Aranovitch M, Blazer S, Zimmer E Z 2009Pediatrics 128 e921.
　　[2] Jiang L, Li H 2012 Chin. J. Neonatol. 27 289 （in Chi-nese） [蒋犁， 李函 2012 中国新生儿科杂志 27 289].
　　[3] Faye P M, De Jonckheere J, Logier R, Kuissi E, JeanneM, Rakza T, Storme L 2010 Clinical J. Pain 26 777.
　　[4] Yoo C S, Yi S H 2004 J. Korean Phys. Soc. 44 561.
　　[5] Li J, Liu D Z 2012 Acta Phys. Sin. 61 208701 （in Chi-nese） [李锦， 刘大钊 2012 物理学报 61 208701].
　　[6] Zhuang J J, Ning X B, Zou M, Sun B, Yang X 2008 ActaPhys. Sin. 57 2805 （in Chinese） [庄建军， 宁新宝， 邹鸣，孙飙， 杨希 2008 物理学报 57 2805].
　　[7] Weissman A, Zimmer E Z, Aranovitch M 2012 P?ug.Archiv-European J. Physiol. 464 593.
　　[8] Huo C Y, Zhuang J J, Huang X L, Hou F Z, Ning X B2012 Acta Phys. Sin. 61 190506 （in Chinese） [霍铖宇， 庄建军， 黄晓林， 侯凤贞， 宁新宝 2012 物理学报 61 190506].
　　[9] Peng C K, Havlin S, Stanley H E 1995 Chaos 5 82.
　　[10] Tang Y F, Liu S L, Jiang R H, Liu Y H 2013 Chin. Phys.B 22 030504.
　　[11] Webber C L, Zbilut J P 1994 J. Appl. Physiol. 76 965.
　　[12] Eckmann J P, Kamphorst S O, Ruelle D 1987 Europhys.Lett. 4 973.
　　[13] Richman J S, Moorman J R 2000 Am. J. Physiol.: Heartand Circulat. Physiol. 278 H2039.
　　[14] Cao B, Xiang Y P, Lü X Q, Zeng M, Huang S S 2008Chin. Phys. B 17 865.
　　[15] Grassberger P, Procaccia I 1983 Phys. Rev. Lett. 50 346.
　　[16] Wang J S, Yuan J, Li Q, Yuan R X 2011 Chin. Phys. B20 050506.
　　[17] Wang G S, Zhong Y X 2001 Acta Electron. Sin. 10 1397（in Chinese） [王国胜， 钟义信 2001 电子学报 10 1397].
　　[18] Chang C C, Lin C J 2011 ACM Trans. Intellig. Syst.Technol. 2 27.
　　[19] Sokolova M, Lapalme G 2009 Inform. Process. Man-agem. 45 427.
　　[20] Oberlander T F, Grunau R E, Whit?eld M F, FitzgeraldC, Pit?eld S, Saul J P 2000 Pediatrics 105 e6.
　　[21] Ding L J, Peng H, Cai S M, Zhou P L 2007 Chin. Phys.Lett. 24 2149.
　　[22] Peng C K, Havlin S, Stanley H E, Goldberger A L 1995Chaos 5 82.
　　[23] Melillo P, Bracale M, Pecchia L 2011 Biomed. Engineer.Online 10 96.