摘要:采用分子动力学模拟方法比较了最新版CHARMM和AMBER (包括bsc1和OL15) 力场对水溶液中B-DNA到A-DNA转化过程的影响, 利用扩展自适应偏置力 (eABF) 方法计算了转化过程的自由能变化。研究结果表明, 在不同力场下, 水环境中的DNA最稳定结构存在差异, AMBER力场比CHARMM力场更符合实验结果。AMBER力场下DNA最稳定结构的小沟较窄, 稳定于B构型;而CHARMM力场下DNA最稳定结构的小沟较宽, 介于B构型与A构型之间。通过分析DNA周围离子及水的分布情况发现, CHARMM力场下DNA小沟周围的离子密度明显低于AMBER力场, 不能很好地抵消2条磷酸骨架之间的排斥作用, 这是CHARMM力场下小沟较宽且趋向A构型的主要原因。
关键词:B-DNA; A-DNA; 构型转变; CHARMM力场; AMBER力场; 自由能计算;
Effect of Different Force Fields on B-DNA to A-DNA Conversion
Abstract:The aim of the present work is to investigate and compare the effect of the latest CHARMM and AMBER force fields (including bsc1 and OL15) on the B-DNA to A-DNA conversion through exploring the free-energy changes of the conversion process. The extended adaptive biasing force (e ABF) method was utilized to perform the free-energy calculations. The results showed that the free-energy profiles characterizing the transition differ significantly for these two force fields. The AMBER force field performs better than the CHARMM force field in aqueous solution. The structure near the global minimum of the free-energy profile by the AMBER force field presents B-form, in agreement with the experimental results, while the most stable structure by the CHARMM force field locates between A-and B-form. Deep analysis of the radial distribution functions of the counterions around DNA reveals that the distribution of counterions in minor groove using the CHARMM force field is lower than that using the AMBER force field. Therefore, for the CHARMM force field, the repulsion of phosphates backbone could not be properly counteracted by counterions, as a result, the minor groove becomes wider, causing a slight conformational change towards A-form.
Keyword:B-DNA; A-DNA; Conformational conversion; CHARMM force field; AMBER force field; Free-energy calculation;
DNA作为生命信息传递的载体, 主要存在B-DNA, A-DNA和Z-DNA 3种形式[1].通常, 在水活度较高的环境 (如细胞) 中, DNA主要以B构型的形式存在。A-DNA则主要存在于水活度较低的环境 (如高盐或高乙醇溶液) 中, 当DNA与RNA配对时, 同样会呈现A构型[2].B构型与A构型DNA的结构如图1所示, 两者均呈现右旋状态, 但A构型小沟较宽, 螺旋较短, 呈现更紧密的螺旋状态。DNA结构的改变与生命活动息息相关, 分子动力学 (MD) 模拟被广泛应用于研究DNA结构改变的机理[3,4].而分子动力学模拟的准确性极大程度上依赖于分子力场的精确程度。CHARMM[5,6], AMBER[7,8], GROMOS[9]及OPLS[10]等力场应用于生物大分子体系已较为成熟。对于DNA, 应用较广泛的力场包括CHARMM和AMBER力场, 其中AMBER力场中的bsc1[7]和OL15[8]力场作为描述DNA的最新版力场被广泛应用。随着力场的不断优化与发展, 其参数的准确性不断提高, 但不足依然存在, 因此发现并改进现有力场的不足是优化力场参数的目标。已有研究结果表明, CHARMM力场描述DNA, 其结构倾向于A构型, AMBER则稳定于B构型[11].因此, 不同力场的应用范围存在差异, 通常, 在水环境中AMBER力场能够更好地描述B构型, 但在水活度较低的环境中, CHARMM力场对A-DNA的描述则更加准确, 与实验结果相吻合[12,13].虽然不同力场下的结构信息研究得比较详细, 但对该现象的本质解释并不十分清楚。同时, 随着力场参数的发展, 不断有新的力场被提出并广泛应用[7,8].
为了深入研究最新版CHARMM和AMBER力场对DNA构型转变的影响, 本文采用分子模拟结合自由能计算的方法[14,15]比较了不同力场下水溶液中B-DNA到A-DNA转化的自由能变化。通过自由能计算可以实现对B构型到A构型转变过程的分析, 结果表明, CHARMM力场下的DNA小沟较宽, 与实验结果存在差异, 采用径向分布函数对该现象进行分析, 发现不同力场下DNA周围的离子分布存在较大区别, 不同的离子分布是造成DNA稳定结构存在差异的主要因素。
1、理论和方法
1.1 模型建立
B-DNA和A-DNA的初始结构由AMBER提供的Nucleic Acid Builder插件构建, 序列分别为GCGCGC和ATATAT.将构建好的DNA模型置于带有周期性边界条件的水立方盒子中, 每个体系加入10个K+作为抗衡离子, 盒子大小约为6.1 nm×6.0 nm×6.4 nm, 每个体系的原子数均为20000个左右。用于模拟自然的生理环境。AT序列 (PDB code:4J2I) 以及GC序列 (PDB code:1QC1) 的晶体结构参考自蛋白质晶体结构数据库[16,17].
1.2 动力学模拟
采用NAMD2.12软件进行MD模拟[18], 分别使用CHARMM36力场、AMBER-OL15力场和AMBER-bsc1力场参数描述DNA;使用TIP3P模型[19]中的参数描述水分子。采用SKAKE/RATTLE算法[20,21]将非水分子中含有氢原子的共价键的长度限制在其平衡值, 采用SETTLE算法[22]保持水分子的刚性。采用恒温恒压的Langevin动力学方法和Langevin活塞方法[23]将温度和压力分别控制在300 K和1.01×105Pa.范德华截断半径为1.2 nm, 长程静电相互作用采用粒子网格埃瓦尔德 (PME) 方法计算。对运动方程积分的时间步长为2 fs, 每个体系在自由能计算之前均经历了2000步的能量最小化过程。从自由能计算结果中选取最稳定结构进行10 ns的平衡模拟, 应用该轨迹进行DNA结构的参数分析及抗衡离子和水分子的径向分布分析。采用VMD软件[24]进行轨迹分析。应用CURVES+软件[25]进行DNA结构参数分析, 分析过程中DNA两末端分别除去两对碱基, 选取中间残基进行分析。
1.3 自由能计算
采用扩展自适应偏置力 (e ABF) 方法计算了转化过程的自由能变化[15], 以ΔRMSD (RMSDB-RMSDA) 作为该转化过程的反应坐标[26].选取DNA上所有重原子作为RMSD计算的参考原子, 标准B-DNA与标准A-DNA的RMSD差值为0.3 nm, -0.3<ΔRMSD<0.3.当ΔRMSD<0时, DNA的结构偏向于B构型;当ΔRMSD>0时, DNA结构偏向于A构型。为了提高计算效率, 反应路径均被分为2个窗口:-0.3<ΔRMSD<0和0<ΔRMSD<0.3.每个窗口的模拟时间为150 ns, 每个体系的模拟时间为300 ns, 总模拟时间为1.2μs.
2、结果与讨论
2.1 自由能曲线
图2 (A) 给出了ATATAT序列B-DNA到A-DNA转变的自由能变化。对于AMBRER力场 (包括bsc1力场和OL15力场) , 最稳定的结构为B-DNA, bsc1力场与OL15力场对应的ΔRMSD值分别为-0.14和-0.15 nm, 如图3 (A) 和 (C) 所示, 其结构非常相似。对于CHARMM力场, 存在一个范围较广的低能区, 由提取能量最低点的结构[图3 (B) ]可见, DNA两末端的氢键破坏较为严重, 氢键的破坏使末端碱基运动较为灵活, 这是导致其稳定结构ΔRMSD值范围较广的原因之一。
图2 (B) 给出了GCGCGC序列的B-DNA到A-DNA转变的自由能变化。可见, 在水环境中不同力场下DNA的最稳定结构存在差异。如图4 (A) 和 (C) 所示, 对于AMBER力场无论是bsc1力场还是OL15力场, B-DNA到A-DNA转化的过程中最稳定的结构为B-DNA, 对应的ΔRMSD值分别为-0.12和-0.13 nm.对于CHARMM力场, 最稳定的结构则偏离标准的B-DNA, 表现为介于B构型与A构型中间的结构[图4 (B) ], 对应的ΔRMSD值为-0.02 nm, 与实验上表现出来的标准B-DNA存在差异。以上结果显示, AMBER力场在描述水溶液中B-DNA到A-DNA转化的最稳定结构更加准确, 该结果与旧版力场的模拟结果类似[12,13], 且bsc1力场与OL15力场结果几乎相同, 因此, 下面只选取bsc1力场进行分析。
2.2 DNA结构参数分析
为了研究在不同力场下DNA全局能量最小点的稳定结构, 提取出全局能量最低点的代表结构进行平衡模拟并分析其结构参数。将不同序列DNA的结构参数与晶体结构进行了比较 (表S1, 见本文支持信息) , 结果表明, 对于 (AT) 6序列, AMBER力场下的绝大部分结构参数能够更接近实验结果。而对于 (GC) 6序列, CHARMM和AMBER力场对不同参数的精确程度不同。其中不同力场差距较大的是大沟和小沟的宽度, 为了进一步探究其原因, 进行了深入分析。
为了进一步探究DNA在不同力场下的结构差异, 对DNA大沟和小沟的宽度进行了统计分析。图5描述了不同力场下不同碱基序列的大沟宽度分布情况, 发现对于 (AT) 6序列, bsc1力场下的大沟宽度分布范围为1.1~1.4 nm, 与晶体结构基本吻合;但CHARMM力场则出现较窄的大沟宽度, 与晶体结构存在差异[图5 (A) ].对于 (GC) 6序列, bsc1力场下的大沟宽度相较于晶体结构略宽, CHARMM力场下的大沟宽度与晶体结构较为相似[图5 (B) ].
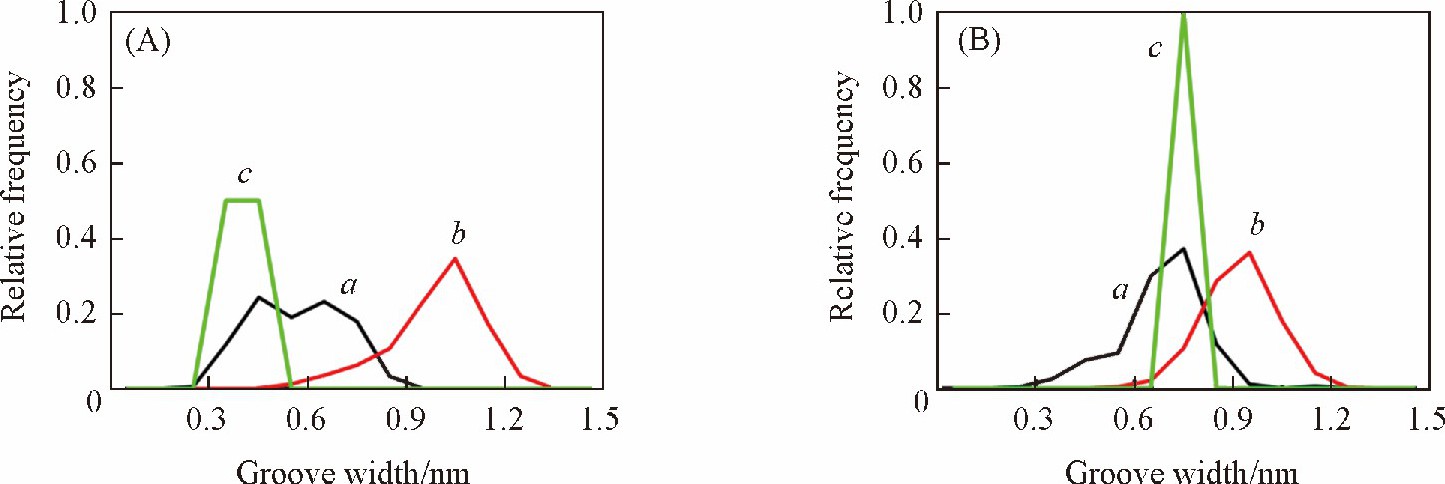
图6描述了DNA小沟宽度的分布情况, (AT) 6序列晶体结构的小沟宽度分布范围在0.3~0.6 nm之间, bsc1力场从一定程度上能够反映晶体结构的小沟宽度, 但是依然存在小沟宽度偏大的现象;但对于CHARMM力场, 小沟宽度分布在0.6~1.3 nm之间, 该结果完全偏离晶体结构提供的信息[图6 (A) ].对于 (GC) 6序列, bsc1力场能从一定程度上反映晶体结构的小沟宽度, 但CHARMM力场下的小沟宽度在分布上明显右移, 呈现较宽的小沟宽度[图6 (B) ].可见, bsc1力场对DNA小沟宽度的描述更为准确, 而CHARMM力场下不同序列的小沟宽度均大于晶体结构。由此可见, AMBER力场 (bsc1) 参数下DNA大沟和小沟的宽度明显比CHARMM力场更加精确。
2.3 抗衡离子对DNA结构的影响
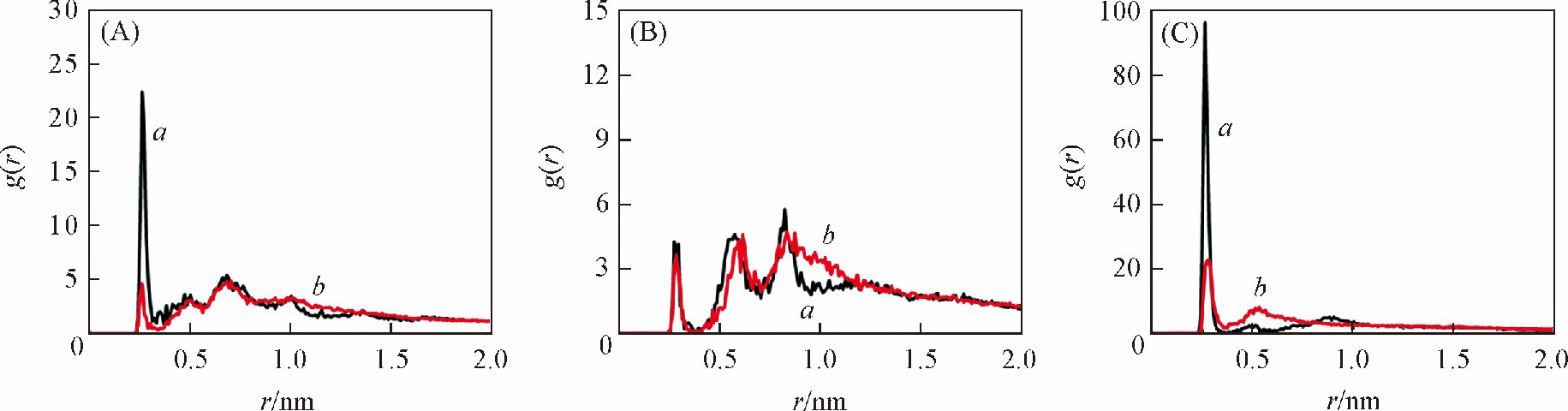
为了探究不同力场下大沟和小沟宽度存在较大差异的原因, 对DNA周围抗衡离子的分布进行了探究。图7和图8分别描述了 (GC) 6序列与 (AT) 6序列在不同力场下DNA骨架、大沟和小沟周围的离子分布情况。由图7 (A) , (C) 和图8 (A) , (C) 可见, 无论是 (GC) 6序列还是 (AT) 6序列, bsc1力场下骨架及小沟周围的离子分布密度均明显高于CHARMM力场。bsc1力场下紧密的离子分布更好地中和了磷酸骨架上的负电荷, 降低了2条磷酸骨架之间的静电排斥作用, 因此与CHARMM力场相比, bsc1力场下的DNA结构小沟的宽度较窄。可见, CHARMM力场不能准确描述小沟宽度的主要因素是, 在CHARMM力场下阳离子在小沟的分布较少, 导致带负电荷的磷酸骨架静电排斥较大, 小沟变宽。
由图7 (B) 和图8 (B) 可见, 对于相同序列, bsc1力场和CHARMM力场下离子在DNA大沟周围的分布密度差别不大, 然而 (GC) 6序列与 (AT) 6序列之间却存在较大差异。根据文献[27]报道, 对于 (GC) 6序列的DNA, 离子在大沟的分布密度高于 (AT) 6序列, 这在模拟中也得到了很好的验证。同时, 小沟周围的离子分布对于不同的碱基序列也差别较大, 由图7 (C) 和图8 (C) 可见, 对于 (AT) 6序列的DNA, 离子在小沟分布的倾向明显高于 (GC) 6序列, 离子在小沟周围的紧密分布更好地中和了磷酸骨架的负电荷, 降低了静电排斥作用, 使小沟变窄, 这很好地解释了实验上 (AT) 6序列DNA的小沟宽度小于 (GC) 6序列的现象。可见, 离子在DNA周围的分布情况是影响DNA大沟和小沟宽度的重要因素。
2.4水分子对DNA结构的影响
DNA周围水分子的分布情况同样对DNA的结构具有较大的影响。对于 (GC) 6序列, 不同力场下DNA周围水分子的分布相差不大 (图9) ;但对于 (AT) 6序列, CHARMM力场下DNA的大沟和小沟周围的水分子分布较多 (图10) .为了探究水分子对DNA结构的影响, 我们提取了平衡模拟中DNA的典型结构, 由图3 (B) 可见, DNA末端碱基氢键被水分子破坏较为严重。因此, 对于CHARMM力场, (AT) 6序列末端碱基的氢键易被周围的水分子破坏, 这也是 (AT) 6序列大沟和小沟周围水分子分布较多的原因。对于碱基之间存在3条氢键的 (GC) 6序列, 相比于形成2条氢键的 (AT) 6序列更加稳定, CHARMM力场与bsc1力场下DNA周围水分子的分布情况则没有较大区别。
3、结论
利用分子动力学模拟结合自由能计算的方法比较了CHARMM和AMBER力场 (包括bsc1力场和OL15力场) 对水溶液中B-DNA到A-DNA转化过程的影响, 分别得到了不同力场下最稳定的DNA结构。结果表明, 在水环境中不同力场下DNA的最稳定结构存在差异, CHARMM力场下DNA最稳定结构的小沟较宽, 介于B构型与A构型之间;AMBER力场下的DNA小沟较窄, 稳定于B构型。进一步探究了不同力场下DNA稳定结构存在差异的原因, 首先分析了DNA周围离子的分布情况。结果表明, CHARMM力场下DNA小沟周围的离子密度明显低于AMBER力场, 不能很好地抵消磷酸骨架的排斥作用, 是CHARMM力场小沟较宽且趋向A构型的主要原因。进一步分析了水分子的分布对DNA结构的影响, 表明CHARMM力场下的 (AT) 6序列末端碱基之间的氢键被水分子破坏较为严重, 与AMBER力场相比, CHARMM力场下的氢键相互作用较弱。在模拟生理环境的水溶液中AMBER力场能够更好地描述实验现象。研究结果为分子模拟实验设计提供了理论指导, 并对进一步的参数优化提供了帮助。
参考文献
[1]Saenger W., Defining Terms for the Nucleic Acids, Springer, New York, 1984
[2]Ivanov V.I., Minchenkova L.E., Minyat E.E., Frank-Kamenetskii M.D., Schyolkina A.K., J.Mol.Biol., 1974, 87 (4) , 817-833
[3]Mukherjee A., Lavery R., Bagchi B., Hynes J.T., J.Am.Chem.Soc., 2008, 130 (30) , 9747-9755
[4]Dumont E., Wibowo M., Roca-Sanjun D., Garavelli M., Assfeld X., Monari A., J.Phys.Chem.Lett., 2015, 6 (4) , 576-580
[5]Foloppe N., Mac Kerell A.D.Jr., J.Comput.Chem., 2000, 21 (2) , 86-104
[6]Mac Kerell A.D.Jr., Bashford D., Bellott M., Dunbrack R.L.Jr., Evanseck J.D., Field M.J., Fischer S., Gao J., Guo H., Ha S., J.Phys.Chem.B, 1998, 102 (18) , 3586-3616
[7]Ivani I., Dans P.D., Noy A., Pérez A., Faustino I., Hospital A., Walther J., Andrio P., Go1i R., Balaceanu A., Nat.Methods, 2016, 13 (1) , 55
[8]ZgarbováM., Luque F.J., poner J.I., Cheatham III T.E., Otyepka M., Jurecka P., J.Chem.Theory Comput., 2013, 9 (5) , 2339-2354
[9]Soares T.A., Hünenberger P.H., Kastenholz M.A., Krutler V., Lenz T., Lins R.D., Oostenbrink C., van Gunsteren W.F., J.Comput.Chem., 2005, 26 (7) , 725-737
[10]Robertson M.J., Tirado-Rives J., Jorgensen W.L., J.Chem.Theory Comput., 2015, 11 (7) , 3499-3509
[11]Song C., Xia Y.Y., Zhao M.W., Liu X.D., Li F., Ji Y.J., Huang B.D., Yin Y.Y., J.Mol.Model., 2006, 12 (3) , 249-254
[12]Cheatham T.E., Crowley M.F., Fox T., Kollman P.A., Proc.Natl.Acad.Sci.USA, 1997, 94 (18) , 9626-9630
[13]Yang L., Pettitt B.M., J.Phys.Chem., 1996, 100 (7) , 2564-2566
[14]Shen W., Shao X.G., Cai W.S., Chem.J.Chinese Universities, 2016, 37 (10) , 1809-1816 (沈文, 邵学广, 蔡文生。高等学校化学学报, 2016, 37 (10) , 1809-1816)
[15]Fu H.H., Shao X.G., Chipot C., Cai W.S., J.Chem.Theory Comput., 2016, 12 (8) , 3506-3513
[16]Acosta-Reyes F.J., Subirana J.A., Pous J., Sánchez-Giraldo R., Condom N., Baldini R., Malinina L., Campos J.L., Biopolymers, 2015, 103 (3) , 123-133
[17]Timsit Y., Moras D., EMBO J., 1994, 13 (12) , 2737
[18]Phillips J.C., Braun R., Wang W., Gumbart J., Tajkhorshid E., Villa E., Chipot C., Skeel R.D., Kale L., Schulten K., J.Comput.Chem., 2005, 26 (16) , 1781-1802
[19]Jorgensen W.L., Chandrasekhar J., Madura J.D., Impey R.W., Klein M.L., J.Chem.Phys., 1983, 79 (2) , 926-935
[20]Ryckaert J.P., Ciccotti G., Berendsen H.J., J.Comput.Phys., 1977, 23 (3) , 327-341
[21]Andersen H.C., J.Comput.Phys., 1983, 52 (1) , 24-34
[22]Miyamoto S., Kollman P.A., J.Comput.Chem., 1992, 13 (8) , 952-962
[23]Feller S.E., Zhang Y., Pastor R.W., Brooks B.R., J.Chem.Phys., 1995, 103 (11) , 4613-4621
[24]Humphrey W., Dalke A., Schulten K., J.Mol.Graphics, 1996, 14 (1) , 33-38
[25]Lavery R., Moakher M., Maddocks J., Petkeviciute D., Zakrzewska K., Nucleic Acids Res., 2009, 37 (17) , 5917-5929
[26]Banavali N.K., Roux B., J.Am.Chem.Soc., 2005, 127 (18) , 6866-6876
[27]Hamelberg D., Williams L.D., Wilson W.D., J.Am.Chem.Soc., 2001, 123 (32) , 7745-7755