摘 要: 对水工结构设计中概率可靠度模型的局限性问题, 提出了不确定性信息要求较低时的非概率可靠度理论, 并以实例验证了该方法的实用性与可靠性, 从而完善了目前可靠度理论分析方法。结果表明:该计算方法具有较强的实用性, 可将复杂问题简单化并且能够符合理论规律, 研究成果可为水工结构设计提供一定决策依据, 为概率极限状态的判别提供理论支持。
关键词: 水工结构设计; 可靠度; 指标分析; 水电站;
Abstract: To overcome the limitation of probabilistic reliability model in hydraulic structure design, a non-probabilistic reliability theory with low uncertainty information requirement is proposed in this paper, and the practicability and reliability of this method are verified by an example, thus to improve the present reliability theory analysis method.The results show that the calculation method has strong practicability, can simplify complex problems and conform to the theoretical rules.The research results can provide certain decision-making basis for hydraulic structure design, and supply theoretical support for the discrimination of probability limit state.
Keyword: hydraulic structure design; reliability; index analysis; hydropower station;
0 引言
单一安全系数法为过去水工结构设计的常用方法, 该方法具有概念明确、计算简便等优点。然而, 这种方法处理问题时在理论上其本身存在一定的缺陷, 对于水利工程边坡或水工结构真实的安全状态与稳定程度不能较好的作出评判[1,2,3,4]。随着科技的进步和时代的发展, 对结构安全状态综合考虑各种随机因素的可靠性理论得到发展和应用。概率统计理论为可靠性计算不确定性问题的常用方法, 该方法对于处理分析结构稳定性、刚度、强度等问题具有明显的优势, 其基本原理是考虑各因素对结构极限状态的影响作用, 如材料强度、外部荷载、结构抗力以及杆件内力等, 然后对结构可靠性利用失效概率衡量。在水工结构设计中通常是以概率论为计算方法, 因此需要大量的信息和数据, 然而水工结构因具有的独特性、复杂性和不确定性等, 有效数据往往较少, 所以应用于实际工程时还存在较大的困难。据此, 文章对目前水工结构可靠性分析中常见的问题, 利用非概率可靠性分析法处理[5,6,7,8]。
1 可靠度理论分析
1.1 传统的理论方法
重力坝在各种环境条件下通常以强度与稳定性破坏两种形式出现, 因此可从这两个方面进行可靠度分析, 分析过程如下:
1.1.1 稳定可靠度分析
承载力极限状态为水工结构抗滑移稳定性分析的判断基础, 为维持坝体整体稳定性主要是利用其自重形成的抗滑力。为便于计算在分析过程中, 坝体和滑动面往往被假定为刚体与胶结面状态, 因此滑动力和阻滑力可分别作为效应函数与抗力函数, 此时可利用下述方程描述抗滑稳定性状态:

式中:f、c、l分别为基岩抗剪摩擦系数、抗剪断内聚力与坝基宽度;W、P分别为计算面上荷载垂直分力与水平力总和;
影响结构设计的因素较多, 准确可靠的结构体系往往较为复杂, 相关文献对极限状态设计采用概率理论分析。利用可靠度作为反映结构体系的重要参数, 并构造可靠度与极限状态之间的数学关系。该可靠度方法主要包括永久、可变与偶然3种荷载、正常使用与承载力极限2中状态、5类分项系数和3个安全等级。坝体工程是结合工程经验和优化分析方法, 综合考虑其破坏特征、经济损失、重要程度等因素而综合确定的分项系数, 承载力极限状态方程, 如下所示:
式中:Sd (·) 、Rd (·) 分别为作用组合效应和结构抗力设计值函数;γ0、φ分别为结构重要性系数和设计状态系数;γdn、Gk、Qk分别为第n种组合的结构系数、永久作用与可变作用标准值;γG、γQ、ak分别为永久荷载与可变荷载分项系数, 集合参数标准值。
但是在实际应用过程中该方法仍存具有较多的分项系数, 其计算较为繁琐, 因此单一系数法得到研究应用。文献提出可引入安全系数K作为γ0、γdn、φ的综合评判, 所以可有效结合单一系数与分项系数法, 从而实现了简化运算。
1.1.2 强度可靠度计算
保证混凝土重力坝结构安全的重要参数为材料强度, 为保证重力坝综合效益的发挥应充分利用混凝土抗压强度高的特点。对重力坝上、下游边缘的垂直应力利用强度可靠性分析方法, 计算方程为:
式中:σyu、σyd分别为重力坝上、下游边缘的垂直正应力;W、M、T分别为计算界面上部全部荷载的垂向分力总和及其对计算截面的形心力矩之和、坝底宽度。
利用此方法可计算坝体材料的应力值并满足相关标准规范的强度指标, 即R>S, 同理对强度可靠度考虑分项系数的表达形式为:
1.2 水工结构中的不确定性
随机性处理不确定性问题为概率可靠度模型的主要方法, 在存在大量实测结构自身荷载与抗力参数的条件下, 利用β度量结构可靠性具有明显的优越性。然而, 在水工结构中遇到的不确定性问题通常不能利用较为精确的概率理论处理分析。
基岩中的渗水压力与大坝排水系统、帷幕灌浆质量以及地质结构等因素相关, 也是一种具有较大变化区间的荷载。在设计阶段因缺乏相应的实测资料, 因此较难对统计参数与概率分布进行计算。温度荷载与日照、水温与气温等变化相关, 通常难以准确估计该参数数值, 因此也作为变量处理。地震荷载具有较大的变异特性, 仅能综合考虑多种因素的影响给出合理的范围。
在大坝设计阶段利用极限拉伸与弹性模量试验设计混凝土配合比, 由于样本较少所以只能给定平均值。在施工阶段对混凝土强度进行取样测试, 可获得充分的数据资料, 因此可统计分析其力学参数。而在实际过程中影响坝体质量的关键因素为平仓振捣, 因此所选择的力学参数并不能真实、客观反映坝体质量状况, 概率可靠度理论在一定程度上受到限制[9]。
基岩破坏通常为造成坝体失稳的主要因素, 所以大坝可靠性与基岩抗力具有较为密切的相互关系。影响基岩承载力的关键因素有基岩内部存在的断层和软弱夹层, 岩土体物质具有较为复杂的物理力学、结构和组成要素, 并且还处于复杂的地下水与地应力环境内, 因此在设计阶段对基岩与夹层内部软弱构造面的黏聚力、摩擦系数仅仅依靠少量的探硐与钻孔存在较大的困难。在基岩稳定性实际工程分析时, 对于渗透压力系数、构造面产装、黏聚力、抹茶系数以及连通率等参数的实测资料较为, 通常难以准确得到统计参数和概率分布, 从而影响模型的分析结果。
1.3 概率可靠度模型分析
根据以上分析和相关研究, 可分别从以下方面探讨影响概率可靠度分析的主要因素:在实际工程中需要根据收集的数据进行分布拟合或参数估计确定统计参数, 样本数据与统计结果具有密切关系, 并且函数运算与随机变量确定的统计参数通常存在较大的偏差;分布概率参数对失效概率具有较为敏感的影响, 通常最终的分析结果受随机变量分布函数的影响最为明显, 真实函数在运算后不服从正态分布并且难以确定其分布特征;在10-5量级的失效概率, 通常难以处理器数值, 仅仅在信息充足的情况下应用概率模型。根据不确定性信息较少和模型可靠性分析可知, 利用概率可靠度模型设计水工结构仍存在一定的局限性和不足, 因此需改进和完善目前的分析方法, 对此可利用凸集模型的非概率可靠度理论进行分析处理。
1.4 非概率可靠性理论
针对概率可靠性理论难以验证结果且要求统计数据较多的问题, Yakov Ben-Haim提出了非概率可靠度的概念, 即:利用凸集合模型描述不确定性信息, 通过分析得到响应范围提出了安全度指标。概率为判定传统可靠性的主要依据, 并按照失效概率越低则系统越可靠的原则, 而非概率可靠性认为系统抗干扰能力越强或性能波动范围越低, 则可靠性越好, 因此也可称为稳健可靠性。在处理不确定程度较严重和不确定性信息较少的工程问题时, 该理论具有较强的适用性与科学性。通过一定的手段将体系负面性能可能发生的概率降低至可允许区间为传统方法的主要目标, 而非概率可靠性则是对系统性能要求在允许范围浮动, 主要反映在如下方面:对结构可利用统计信息较少的条件下, 实现较为准确、科学的可靠性分析, 并解决在实际应用过程中传统可靠性模型存在的问题, 因此该方法具有较强的实用性与可行性。
文献根据非概率与区间理论, 提出了一种能够衡量体系状态的方法, 首先假定不确定性变量X={X1, X2, …, Xn}为结构向量, 其中Xi为基本变量并且变化区间为 (xil, xiu) 为上、下边界。基于传统概率可靠性引入结构失效准确的功能函数为Z=g (X) =g{X1, X2, …, Xn}, 可证明X={X1, X2, …, Xn}的连续函数为g (X) 时, 相应的Z也为区间变量。如果Zc、Zr分别为函数Z的均值与离差, 则可利用下式反映非概率可靠性指标η:
η值>1, 则函数g (X) 值为正, 可认为结构处于安全可靠状态;η值<-1, 则函数g (X) 值为负, 可认为结构处于失效状态;η值处于-1-1范围时, 可认为结构处于安全或不稳定状态, 考虑到工程安全的实际状况可认为η<1则结构不可靠。因此, 对结构体系可根据参数不确定性判定为可靠与不可靠状态, 结构安全可靠程度随无量纲η值的增大而提高, 可将η作为判定结构可靠度的指标和依据。
2 实例应用
2.1 水电站概况
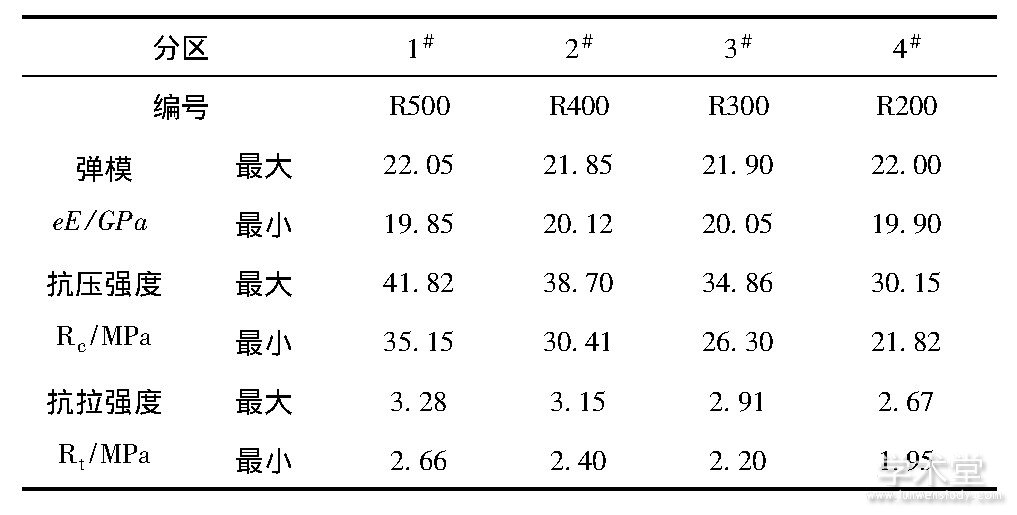
山东省某水电站大坝主要有温度荷载、淤沙压力、坝体重力、水压力以及扬压力等荷载。为获得更多的监测资料并更加高效、全面的获取大坝的工作状态, 在水利大坝建设施工期布设了多个观测检验装置如环境温度、变形、裂缝、渗流量、应力应变、裂缝、渗流、扬压力、上游水位、引张线、垂直监测等仪器装置[10]。大坝高程295m、坝体内摩擦角为22°, 坝体死水位和正常蓄水位分别为1560m和1620m, 总库容和调节库容分别为76.2×108m3、50.1×108m3, 电站装机容量为4500MW且为年调节水库。在正常蓄水位条件下, 对可靠度计算的定值选取为扬压力折减系数和上、下游水位, 坝体力学参数如表1所示。
表1 混凝土双曲拱坝力学参数
2.2 非概率可靠度指标分析
响应面法模拟真实的极限状态曲面主要是利用输入与输出关系来实现, 利用功能函数不能显式大坝的复杂结构特征并且不利于可靠性分析。据此, 可对大坝可靠性分析利用有效原发与响应面法相结合的方法, 即对大坝结构利用有效原发分析并对结构功能函数采用响应面法求解, 然后对结构功能响应的极大值与极小值利用功能函数和数学优化法进行求解, 从而得到非概率可靠度指标计算结果。
对非概率可靠度指标利用ANSYS有限元软件和FORTRAN接口优化程序进行求解, 受文章篇幅限制文章未做详细介绍, 仅给出了可靠度指标计算结果。大坝的可靠度指标较低的区域位于上游区域的坝踵周围, 而坝体的抗拉指标在线弹性与弹塑性分析中的最小值分别为-2.05MPa与-0.82MPa, 最小值出现在坝高1/6附近的左坝角上游面。
对各不确定性变量概率分布因缺乏足够的有效信息而无法全部求解, 因此仅对复杂大坝的结构依据各参数变化区间进行分析, 结果显示该分析结果与理论规律保持良好的一致性, 并验证了该方法的可行性与可靠性。
3 结论
1) 对大坝结构利用有效原发分析并对结构功能函数采用响应面法求解, 然后对结构功能响应的极大值与极小值利用功能函数和数学优化法进行求解, 从而得到非概率可靠度指标计算结果。
2) 整个大坝的可靠度指标较低的区域位于上游坝踵附近, 而坝体的抗拉指标在线弹性与弹塑性分析中的最小值分别为-2.05MPa与-0.82MPa, 最小值出现在坝高1/6附近的左坝角上游面。
参考文献:
[1]罗志国, 赵兴健, 张瑞刚.基于可靠度理论的水工结构设计方法[J].水利科技与经济, 2015 (09) :26-28.
[2]朱伯芳.关于可靠度理论应用于混凝土坝设计的问题[J].土木工程学报, 1999, 32 (04) :10-15.
[3]郭书祥, 冯立富.概率可靠性模型的可靠性[J].空军工程大学学报:自然科学版, 2000, 1 (05) :72-74.
[4] 李清富, 高建磊, 乐金朝.工程可靠性原理[M].郑州:黄河水利出版社, 1995:57-58.
[5] 吴世伟.结构安全度与可靠度分析论文集[M].南京:河海大学出版社, 1988.
[6]郭书祥, 吕震宙, 冯元生.基于区间分析的结构非概率可靠性模型[J].计算力学学报, 2001, 18 (01) :56-60.
[7]赵国藩.工程结构可靠性理论与应用[M].大连:大连理工大学出版社, 1996:27-31
[8]张勇, 陈俊, 郭训平.可靠度理论在水工结构应用中的探讨[J].水电能源科学, 2008, 26 (02) :85-87.
[9]马宾.水利工程管理现代化与精细化建设研究[J].黑龙江水利科技, 2017 (04) :48-50.
[10]纪中庭.关于现代水利工程中的生态问题探讨[J].水土保持应用技术, 2016 (01) :22-23.
结构可靠性是研究结构在各种随机因素作用下的安全问题。应用可靠性理论可以解决结构的强度、刚度、稳定性等问题。该理论以概率论、数理统计方法和随机过程理论为基础,从系统角度出发,将结构系统的设计、分析、评价、检测和维护融为一体[1].随着计算机技...