摘要:基于圣维南控制方程组, 针对三峡库区朱沱-坝址河段, 采用θ半隐方法离散动量方程的水位梯度项, 运用欧拉-拉格朗日方法求解动量方程的对流项, 利用有限体积法离散连续性方程, 结合预测校正法将枝状河网稀疏线性系统分解为若干三对角子系统, 建立了一种可实现河网系统速度-压力耦合问题简单、快速及高精度求解的一维枝状河网水流数学模型。选用2005年、2006年实测水位资料对该模型进行率定与验证, 水位计算误差一般<10cm, 流量计算误差一般<5%, 数学模型计算结果与实测资料符合较好, 表明模型精度较高。在单核串行效率测试中, 模型模拟1 a水流过程耗时约23.7 s, 实现了三峡库区枝状河网水动力过程的实时模拟。
关键词:三峡库区; 枝状河网; 一维水动力模型; 水流速度; 实时模拟;
1 研究背景
为快速高效地模拟河网水流过程, 反映河流真实形态, 大量学者已经研究开发了多种一维河网水流数学模型, 建模过程中常见的离散格式主要为六点中心Abbott差分格式及Preissmann四点隐式差分格式等[1-5].这些模型在计算中具有较好的稳定性;计算结果精度较高、可靠性好、适用范围广、可扩展性良好。但是在计算速度与效率方面略有不足, 在模拟较长时段水流运动过程时需花费较长时间, 实时性较差。而在现有诸多实际工程问题中, 尤其在汛期防洪问题及水库实时调度问题中可能需要利用水力学方法进行实时模拟计算, 在此背景条件下, 亟需开发一种高效的河网水流数学模型满足工程需求。为此, 以提高计算效率为目标, 引入粒子追踪思想, 构建通用河网拓扑关系, 研究开发一种显隐式结合的河网水流数学模型。并在此基础上, 建立了长江干流朱沱-三峡坝址河段的河网模型, 计算检验了模型的稳定性、准确性与高效性, 可进行水动力过程的实时模拟。
2 高效求解的河网水流数学模型
2.1 模型原理
2.1.1 控制方程
针对一维河网水力学计算问题, 基于定床假设, 假定波动水面呈渐变趋势, 断面水面线无横比降, 过水断面压力在垂线上满足静水压力分布规律, 河 (渠) 道底坡足够小, 仅考虑水头沿程损失, 且非恒定流阻力可借用恒定流阻力公式进行计算。在上述假定条件的基础上, 可使用圣维南方程组作为水流数学模型的控制方程组, 其基本形式如式 (1) 、式 (2) 所示, 其中式 (1) 为连续方程, 式 (2) 为动量守恒方程。
式中:B为断面水面宽度;η为断面中心水位;Q为断面流量;A为过水断面面积;g为重力加速度;n为河道综合糙率值;R为断面水力半径;t为时间;x为距离。
2.1.2 离散格式
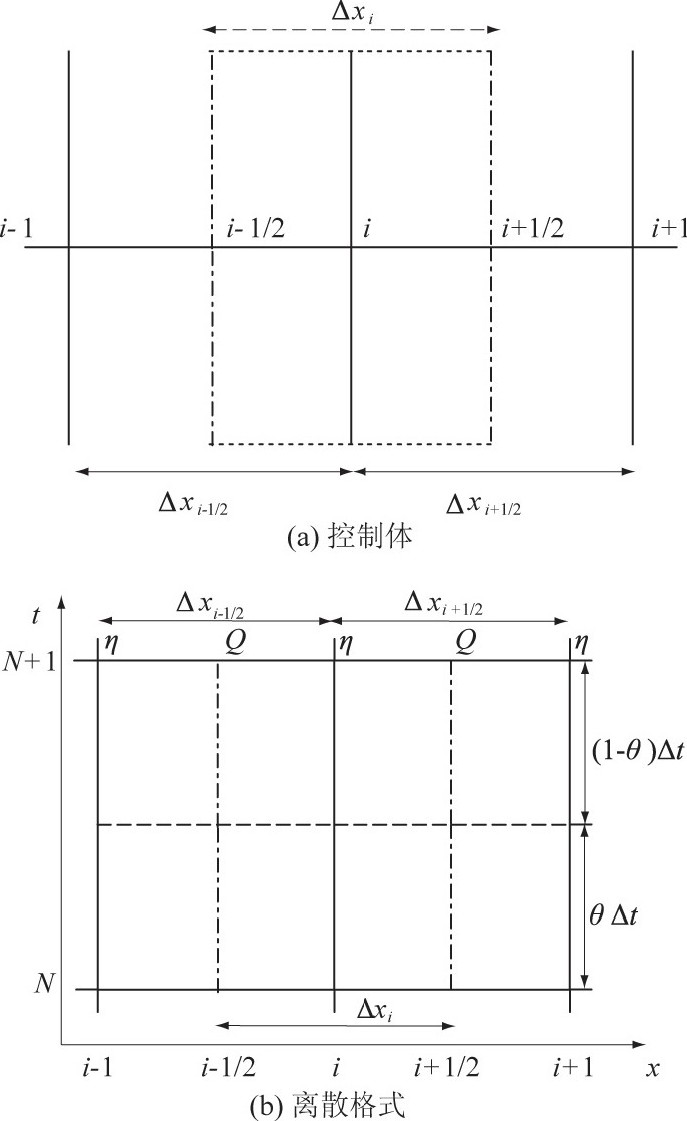
研究采取以断面为中心的方式构建控制体, 其示意图如图1 (a) 所示, 图中竖实线代表断面, 虚线所围成的矩形构成了水位控制体, 竖虚线表示水位控制体的前后流量介面。
在保证模型计算稳定、准确的同时, 亦考虑模型的高效求解, 采用θ半隐的离散格式[6]对动量守恒方程的水位梯度项进行离散, 如图1 (b) 所示。得到简化的动量守恒方程离散形式如式 (3) 所示, 相应得到连续方程的θ半隐离散形式如式 (4) 所示, 对阻力项则采用显式格式进行离散, 其形式如式 (5) 所示。
式中:i为水位控制体编号, 取值为0, 1, 2, …;N为当前时刻, 取值为0, 1, 2, …;N+1为下一时刻;Qi±1/2为第i个水位控制体前后介面中心流量;Ai±1/2为第i个水位控制体前后介面处过水断面面积;θ为隐式因子, 一般取值在0.5~1.0之间;ηi为第i个水位控制体水位;Δxi+1/2表示第i个断面到i+1个断面的距离;Li为第i个水位控制体长度;Ri±1/2表示第i个水位控制体前后介面处水力半径。
2.1.3 欧拉-拉格朗日粒子追踪法
为准确、快速得到各介面流速大小, 引入欧拉-拉格朗日粒子追踪法[7] (ELM) 计算对流项。对于一维水流, 通常以断面中心的状态来描述整个断面的情况, 故可将某一断面概化为其中心处的单一粒子, 推求该粒子在时间、空间内运动的变化。假设从tN时刻到tN+1时刻, 某粒子从位置x运动到位置x', 若不考虑质量损失, 则粒子运动的速率一定, 若想获取该粒子tN+1时刻的运动状态, 则只需获得其在tN时刻所在的空间位置与速率;根据河道水流方向及当前位置的前后断面中心点坐标计算可得到粒子的运动方向。任一粒子随时间、空间变化的运动状态可用式 (6) 来描述。
式中:uj为第j个粒子的速率;degj为第j个粒子的运动方向, 即与水平线所呈的夹角大小;Xi, Yi分别为第i个断面中心点的横坐标和纵坐标。
2.1.4 枝状河网预测校正算法
计算将河网划分成多个河段, 对每个河段运用预测校正法[8], 将单步求解分成2步, 能够在保证计算精度的同时提高计算速度。
(1) 预测步:每一计算时段内, 对每一计算河段, 根据边界条件、上一时段末状态与水力参数求解各控制体水位。
(2) 校正步:将预测步计算得到的各河段末断面的水位作为新的下边界条件, 根据预测步的上边界条件与参数再次求解各断面的水力要素, 由此计算得到各断面各时刻较为准确的水位值。
2.2 模型求解步骤
基于上述离散原理, 结合实测数据资料, 依照地形数据, 构建一维河网水流数学模型, 其求解的主要步骤如下所述。
(1) 构建拓扑关系。根据断面基本信息数据, 建立河道、断面、控制体及计算介面间的拓扑关系, 依据断面平面坐标, 构建断面空间位置结构, 在此基础上, 规定计算正方向。
(2) 初始化参数。读取控制体糙率值、初始水位, 初始化各断面及各计算介面上的水位、流量等水力要素。
(3) 时间步循环计算。每一时间步内: (1) 显式求解动量守恒方程中的对流项与阻力项; (2) 结合动量守恒方程和连续方程, 先构造关于水位ηN+1i-1, ηN+1i, ηN+1i+1的三对角矩阵方程 (经过动量方程和连续方程离散化简, 求解水位的矩阵方程形式Aη=B, 其中矩阵A为三对角矩阵) , 并基于预测校正算法利用追赶法求解隐式水位梯度项部分; (3) 根据动量守恒方程, 将 (2) 中计算所得水位结果回代求解各断面流量; (4) 输出每一时刻各断面的水位、流量、流速、过水面积等水力要素计算结果。
3 实例计算与验证
以长江干流朱沱-三峡大坝坝址河段为研究对象, 计算验证模型的合理性、准确性, 测试模拟时间, 论证实时模拟的可能性。概化计算河段如图2所示, 朱沱-三峡坝址河段长约760 km, 河段自上而下沿程设有朱沱、寸滩、清溪场、万县、庙河5个水文站, 坝址附近凤凰山水位站为坝前水位代表站, 2大支流嘉陵江和乌江的入库控制站分别为北碚站和武隆站, 干流河道库面宽度一般为700~1 700 m, 丘陵峡谷交替变化, 地貌奇特, 地形复杂, 具有一定的代表性[9].模型上边界条件为朱沱站流量过程, 下边界条件为凤凰山站水位过程, 主要中间边界条件为北碚站和武隆站流量过程。
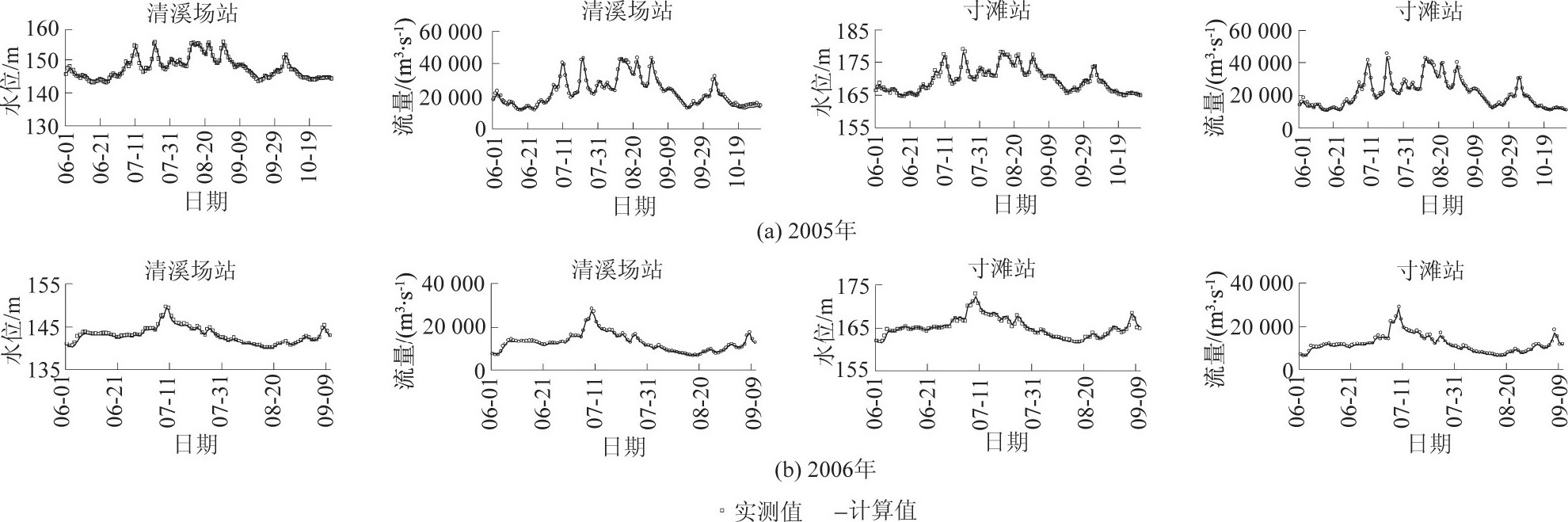
选取2005年6-10月实测数据进行参数率定, 选取2006年6-9月实测数据进行验证, 率定得到计算河段的河道综合糙率值为0.034~0.045.具有代表性的寸滩站、清溪场站的率定与验证结果如图3所示。各站点水位、流量过程的验证结果良好, 水位计算误差一般≤10 cm, 最大误差约为20 cm;流量计算误差一般≤5%, 最大误差约为10%, 数学模型计算结果与实测资料符合较好, 实现了高精度的水流模拟, 模型构建合理。
在此基础上, 以1 a为计算总时段, 测试模型计算效率。计算环境搭建在Windows 7操作系统下, 运用Intel Xeon E5-2697a v4 (clock speed:2.6 GHz) 处理器进行单核计算, 统计50次计算平均耗时约为23.7 s.由此可见, 模型计算效率较高, 多次运算时间差别不大, 稳定性较好, 可以满足三峡库区水动力过程实时模拟的要求, 从运算耗时的角度来看, 模型能用于三峡水库实时调度研究。
4 结语
以实时模拟三峡库区水动力过程为研究目标, 引入欧拉-拉格朗日法处理动量守恒方程的对流项, 采取θ半隐离散格式求解水位梯度项, 运用有限体积法离散连续方程, 在此基础上建立一维河网水流数学模型, 并基于预测校正法利用追赶法求解以河段为单元离散构建的三对角矩阵系统方程组。基于所建模型, 模拟实测数据下三峡库区朱沱-坝址河段水流演进过程, 率定验证了模型具有较好的稳定性与精度, 并通过大量年时段计算, 检验了模型具备实时模拟的能力, 实现了研究目标。
参考文献
[1]谢鉴衡。河流模拟[M].北京:水利电力出版社, 1990:68-72.
[2]汪德颧。计算水力学理论与应用[M].北京:科学出版社, 2011:139-154.
[3]衣秀勇, 关春曼, 果有娜, 等。DHI MIKE FLOOD洪水模拟技术应用与研究[M].北京:中国水利水电出版社, 2014:4-5.
[4]夏军强, 张晓雷, 邓珊珊, 等。黄河下游高含沙洪水过程一维水沙耦合数学模型[J].水科学进展, 2015, 26 (5) :686-697.
[5]陈炼钢, 施勇, 钱新, 等。闸控河网水文-水动力-水质耦合数学模型--Ⅰ。理论[J].水科学进展, 2014, 25 (4) :534-541.
[6]HU De-chao, ZHONG De-yu, WANG Guang-qian, et al.A Semi-implicit Three-dimensional Numerical Model for Non-hydrostatic Pressure Free-surface Flows on an Unstructured, Sigma Grid[J].International Journal of Sediment Research, 2013, 28 (1) :77-89.
[7]HU De-chao, ZHANG Hong-wu, ZHONG De-yu.Properties of the Eulerian-Lagrangian Method Using Linear Interpolators in a Three-dimensional Shallow Water Model Using z-level Coordinates[J].International Journal of Computational Fluid Dynamics, 2009, 23 (3) :271-284.
[8]HU De-chao, ZHONG De-yu, ZHANG Hong-wu, et al.Prediction-Correction Method for Parallelizing Implicit 2D Hydrodynamic Models.I:Scheme[J].Journal of Hydraulic Engineering, 2015, 141 (8) :04015014.
[9]黄仁勇。长江上游梯级水库泥沙输移与泥沙调度研究[M].北京:科学出版社, 2017:14-16.