双圆柱柱间螺旋流的轴向速度流速分布探析

　　摘    要：　为了进一步研究圆柱体间流场水流特性,利用粒子图像测速仪(PIV)对双圆柱体间断面轴向流速的流场进行模型试验,对比分析了不同断面中的轴向速度分布。结果表明,随着与后圆柱体距离的增加,圆柱体间轴向速度分布呈现旋转对称-轴向速度分布均匀化-趋向旋转对称的发展规律;不同直径的测环圆柱体间流场中,下游部分水流在上游导流条引流作用下轴向流速分布逐渐整体偏离管轴中心线;水流沿后圆柱体导流条及支撑体流动至测试范围内,受旋转对称支撑体影响,紧贴后圆柱体支撑体横截面中轴向速度出现负值。

　　关键词：　双圆柱体; 绕流; 轴向速度; 水流特性;

　　Abstract：　In order to further study the water flow characteristics of the flow field between cylinders, a particle image velocimeter(PIV) is used to perform a model test on the flow field of the axial velocity of the two-cylinder section, and the axial velocity distributions in different sections are compared and analyzed. The results show that as the distance from the rear cylinder increases, the trend of axial velocity distribution between cylinders is rotationally symmetric-the axial velocity distribution is uniform-trending to rotational symmetry. In the flow field between the measuring ring cylinders with different diameters, the axial velocity distribution of the downstream part of the water gradually deviates from the center line of the pipe axis as a whole under the action of the upstream persion strip. After the water flows along the guide strip of the rear cylinder and the structure of the support body to the test range, the axial velocity of the support body close to the rear cylinder becomes negative under the influence of the rotationally symmetric support body.

　　Keyword：　two-cylinder; flow around; axial velocity; flow characteristics;

　　管道车是承装固体物料或液体的透明有机玻璃圆柱状载体,两端带有120°旋转对称的金属支撑体,其圆柱体外侧黏附具有一定安放角的导叶,是用于长距离管道水力输送的载体,具有清洁高效,方便快捷的优点。管道车主体为圆柱体状,其周边水流为类圆柱绕流。为了探明圆柱绕流水力特性,国内外诸多学者进行了大量的研究。李永业等[1]分析了圆柱体从静止起动到稳定运行时同心环状缝隙流的分布规律,建立了同心环状缝隙流在动边界条件下的数学模型。张琪琦等[2]、吴剑等[3]在不同环隙比、流量、直径条件下研究了圆柱体绕流的同心圆环状缝隙流场的水力特性。吴新等[4]分析了并列旋转双圆柱不同旋转方式对涡旋脱落的抑制作用;邹帅等[5]利用PIV及染色法研究了圆柱在过渡流下的绕流周期性及流动特性;刘志荣等[6]利用本征正交分解(POD)重建了开缝圆柱的流场并且发现圆柱绕流近区尾流受雷诺数的影响;周潇等[7]发现前置柔性隔板的弯曲变形易改变圆柱绕流尾迹区脱落涡的主频;张宾等[8]通过动力模态分解(DMD)对不同旋转速度比下圆柱绕流流场的各阶模态进行提取;杜晓庆[9]等采用大涡模拟(LES)方法发现高雷诺数下并列双圆柱绕流长随间距的增大产生多种流态结构;王伟等[10]发现脊状结构在雷诺数小于等于1.2×104时能够有效抑制边界层的分离;龚志军等[11]利用非平衡外推法对并列圆柱绕流数值模拟边界条件进行了处理;Canuto等[12]根据雷诺数和自由马赫数得出了圆柱体周围线性流增长率与主导频率的半经验公式;Gao W等[13]提出了具有两个自由端的有限圆柱体的阻力系数与雷诺数的关系。
 

 

　　目前,圆柱绕流主要集中于研究竖向圆柱尾迹流场方面,在横向双圆柱柱间流场的水流特性研究相对较少,缺少带导叶双圆柱引起的柱间螺旋流场研究。为此,本文利用粒子图像测速仪(PIV)对于双圆柱柱间螺旋流的轴向速度流速分布规律进行研究,为双圆柱体周边水流流场研究提供一些理论参考。

　　1 、试验设计

　　1.1、 试验系统

　　本试验开展于太原理工大学水利科学与工程学院水流试验大厅,试验系统主要由抽水及流量调节系统、试验管道系统、测量仪器系统三部分组成,对双圆柱体间轴向流速分布进行模型试验。试验时,从地下水库抽水至钢水箱储水,离心泵从钢水箱抽水至试验管道中并通过电磁流量计的监测进行流量调节直至特定流量,水流流经圆柱体试验测试范围并通过中端U型管道流至尾端钢水箱,形成封闭的水流循环系统。

　　1.2、 试验方案

　　本试验水流流量为40 m3/h,采用150 mm×70 mm(圆柱高×直径)的双圆柱体,圆柱体间距为一个圆柱高,即150 mm,运输管道采用内直径为100 mm的有机玻璃圆管,壁厚为5 mm。使用粒子图像测速仪2D-2C PIV对圆柱体间流场速度分布的进行全程瞬时无干扰采集。试验中,为清晰的展示流场扰动,采用水流跟随性优良的30 μm空心微珠示踪粒子。使用Dynamic Studio软件对试验进行标定、采集、后处理。采集时两帧时间间隔为500 μs,后处理时图像去除背景噪声后使用adaptive PIV方法得到矢量速度,剔除异常值后最终得到质点的速度。采用电磁流量计实时反馈流量数据,离心泵调节试验所需流量。

　　图1 试验系统布置

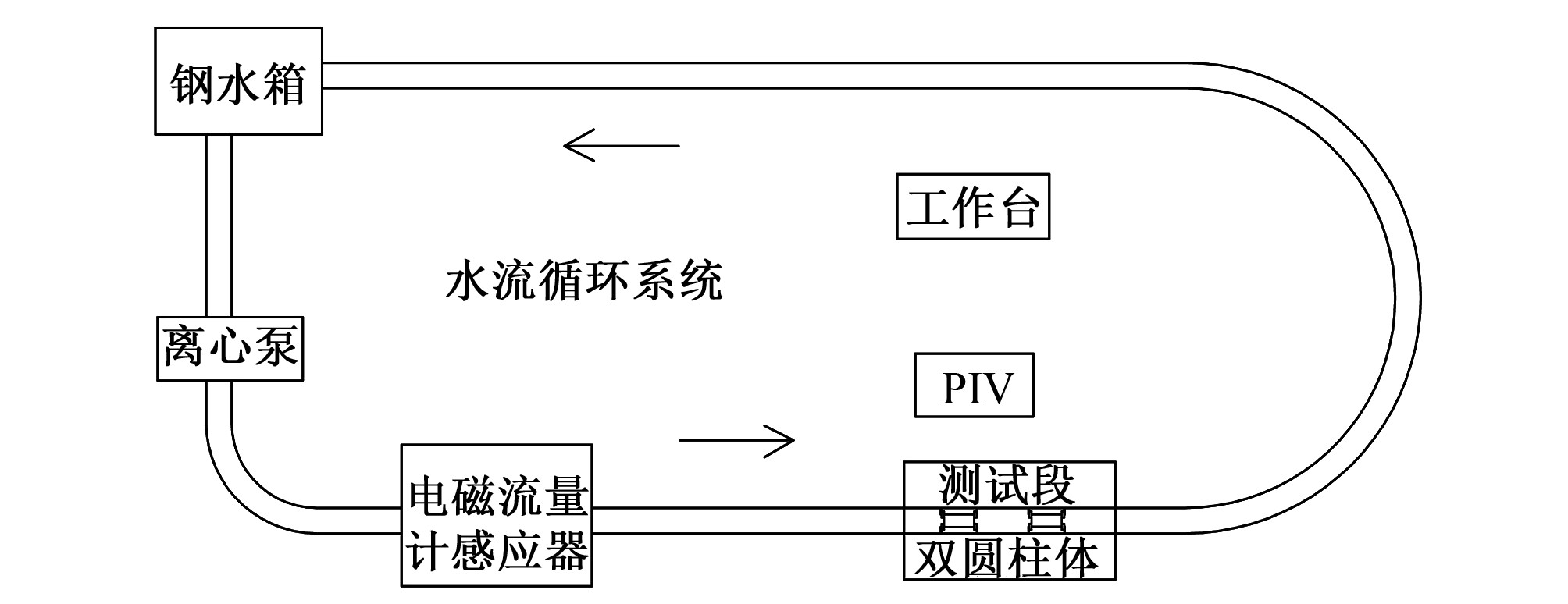
　　Fig.1 Layout of the experimental system

　　1.3 、试验模型

　　本研究采用双圆柱体进行物理实验。圆柱体(见图2)两端安装3个以圆心为中心呈120°旋转对称布置的金属支脚与交错布置的导流条,导流条安放角为25°。水流经支撑体与导流条通过圆柱体,减小水流流经圆柱体的阻力。

　　图2 研究断面位置图

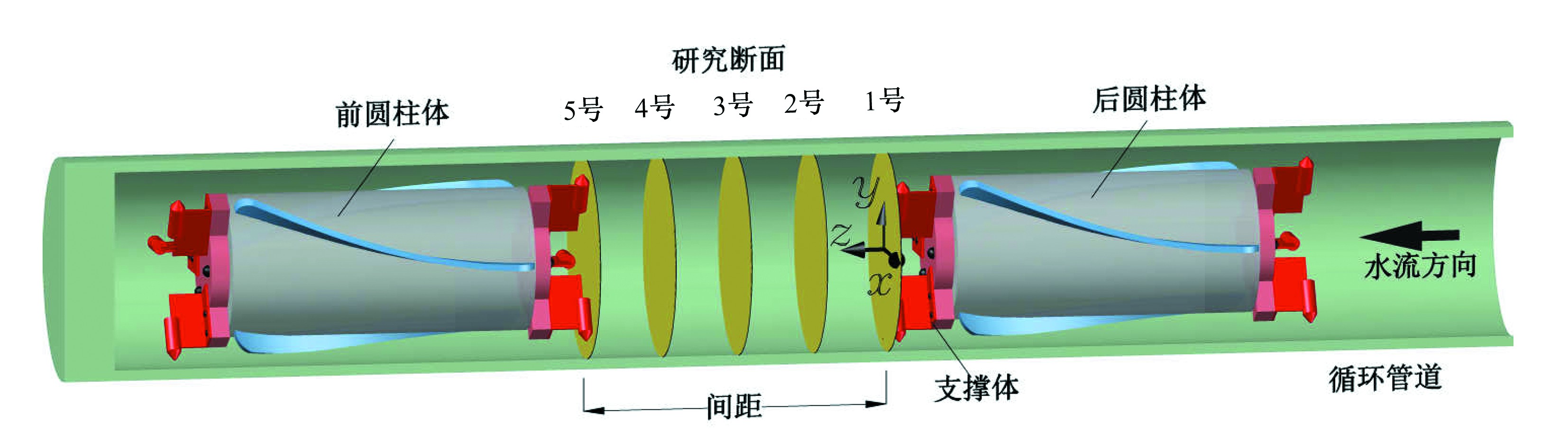
　　Fig.2 Diagram of study section location

　　1.4 、测试范围布置

　　本试验采用极轴测点布置展开不同工况下轴向速度的测量,前圆柱体与后圆柱体间距为一个料筒长度,即150 mm,圆柱体间中每隔37.5 mm设置一研究横截面,共5个研究横截面,第1个和第5个研究横截面分别紧贴后圆柱体末端支撑体及前圆柱体首端支撑体。横截面断面布置见图2。

　　试验坐标布置采用笛卡尔坐标系,原点设置在紧贴后圆柱体支撑体截面圆心位置(见图2),x轴为水平方向,y轴为垂直方向,z轴正方向为沿水流方向。本试验管道内直径为100 mm,在圆心布置半径为9 mm的测环并依次增加,共5个测环,并每隔30°设置一测轴,共12个测轴。测环与测轴交点处即为测点,包括圆心,共61个测点。测点布置图见图3。

　　图3 极轴测点布置示意图

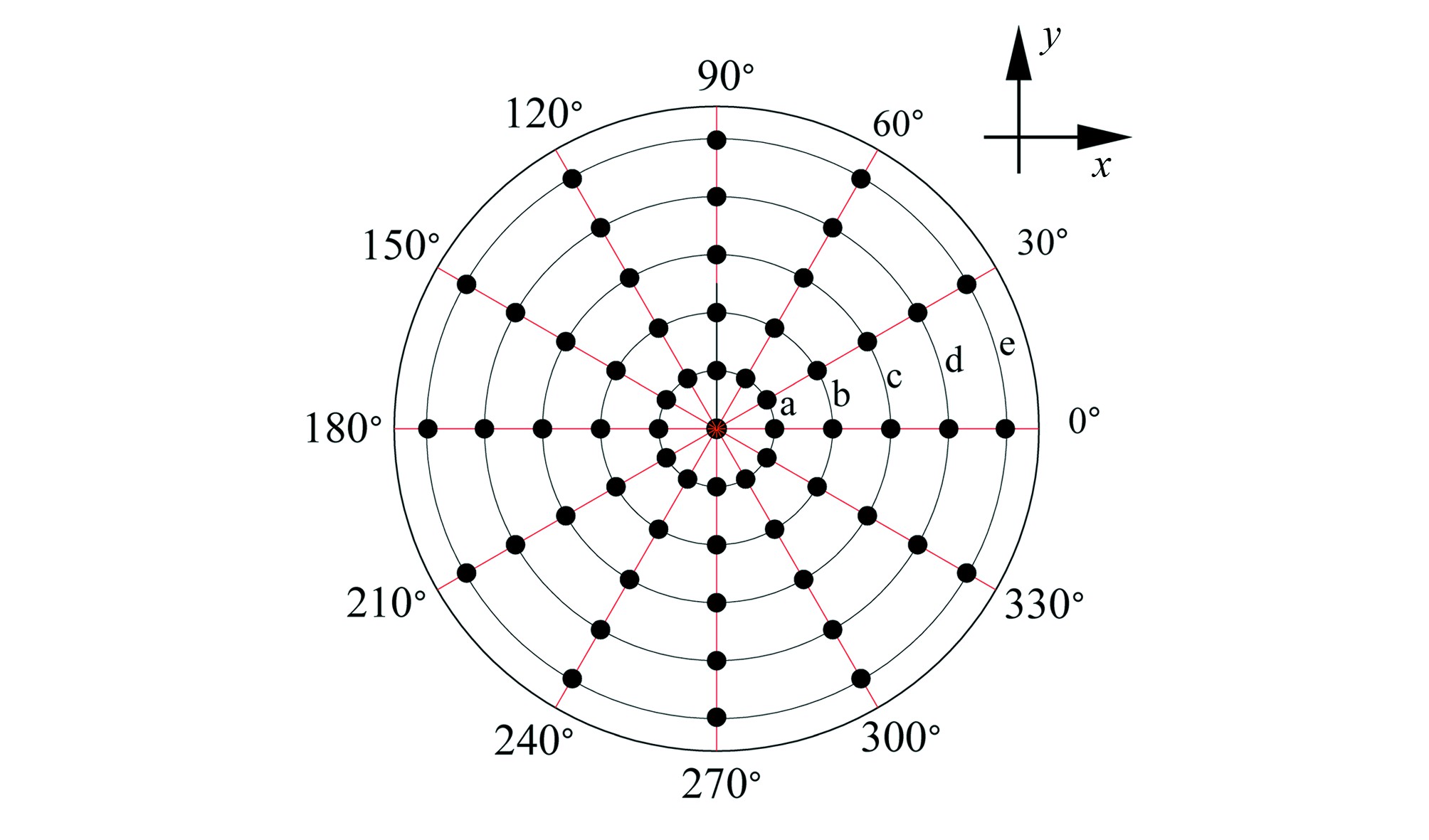
　　Fig.3 Schematic diagram of polar measurement points

　　2、试验分析

　　2.1、 不同横截面轴向流速分析

　　以圆柱体间距分别为0,37.5,75,112.5,150 mm断面为例,分析沿水流方向距离后圆柱体不同距离横截面的水流轴向速度分,具体见图4。

　　从图4中可以看出:

　　(1)水流从后圆柱运动至前圆柱体,水流轴向流速分布整体向截面圆心聚拢,近壁面处轴向流速高速区域呈120°旋转对称向圆心方向逐渐发展扩大直至均匀。圆柱体间轴向速度分布呈现旋转对称-轴向速度均匀化-趋向旋转对称的发展规律。

　　图4 不同横截面轴向速度分布图(单位:m/s)

　　Fig.4 Axial velocity distribution of different cross sections

　　(2)轴向流速整体发展为圆管中心区域流速小,近壁面处间隔120°流速大的分布。紧贴后圆柱体断面旋转对称分布特性最明显。

　　(3)各截面圆管中心区域等值线为稀疏同心圆状,流速梯度较小,轴向速度变化幅度小。水流受后圆柱体料筒阻挡,使得中心区域水流发展受阻。

　　(4)圆管沿圆心至管壁,等值线逐渐密集,流速梯度沿程变大速度值变化迅速。水流受后圆柱体导叶及支撑体的强制导向后,产生绕流现象,使得轴向流速剧烈变化。

　　2.2 、不同测环位置轴向速度分析

　　以直径为9,18,27,36,45 mm测环圆柱侧面测试范围为例,分析圆柱体间轴向流速分布,具体见图5。

　　从图5中可以看出:

　　(1)整体柱状轴向流速上下左右区域均呈现不对称情况。这是由于水流在后圆柱体车身范围内因支撑体与导叶旋转对称布置,下游水流受后圆柱体导流条引流产生周向速度,流速分布因能量的相互传递进行重新分配。

　　(2)测试范围内5个测环柱状展开流速分布图中大致呈现管轴上半部分总体等值线比下半部分等值线密集,下半部分呈现等值线尖角低速区域且随着横截面的递增逐渐缩小至测试范围中心横截面。

　　(3)随着横截面与后圆柱体距离的递增,轴向流速分布趋向均匀化,测试范围内下游部分轴向流速比上游部分流速大,并在上游导叶引流作用下轴向流速分布逐渐整体偏离管轴中心线。

　　图5 相同测环侧面轴向速度分布图(单位:m/s)

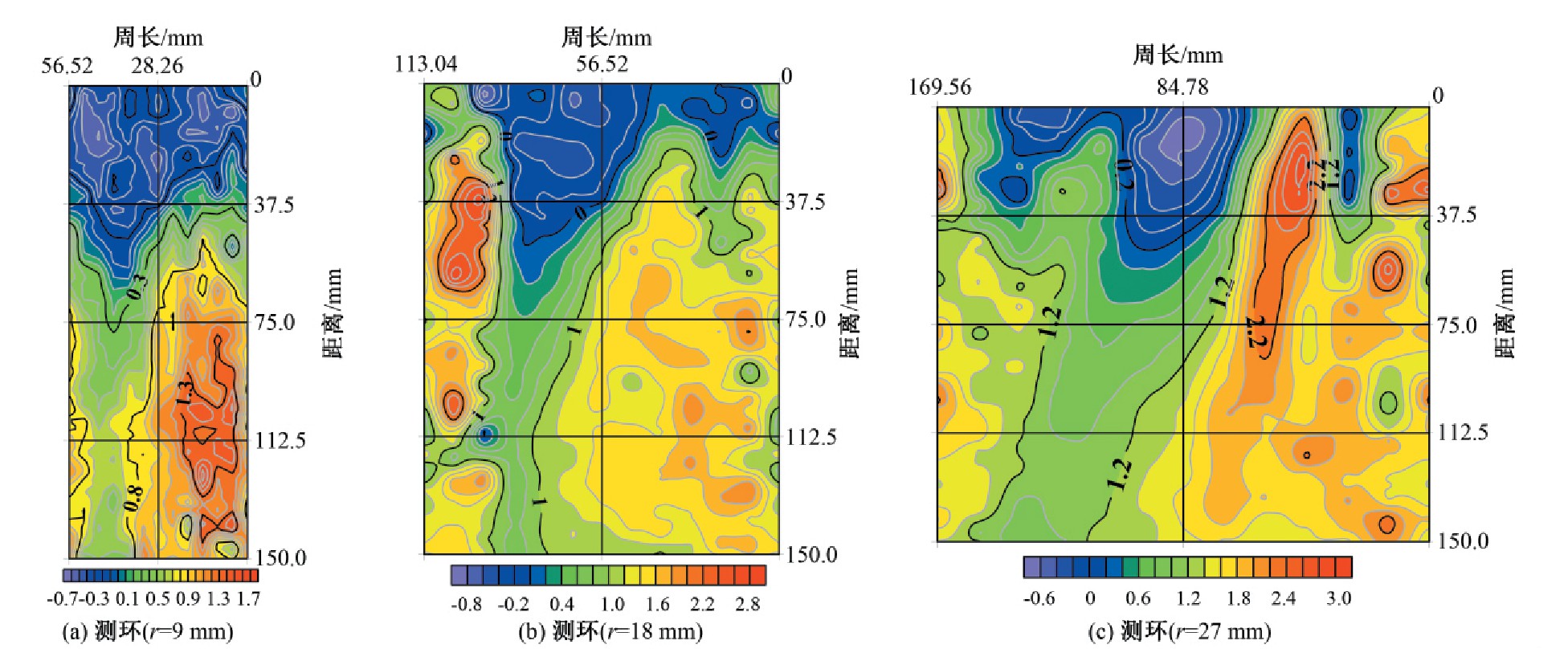
　　Fig.5 Axial velocity distribution on the side of the same measuring ring

　　图5 相同测环侧面轴向速度分布图(单位:m/s)

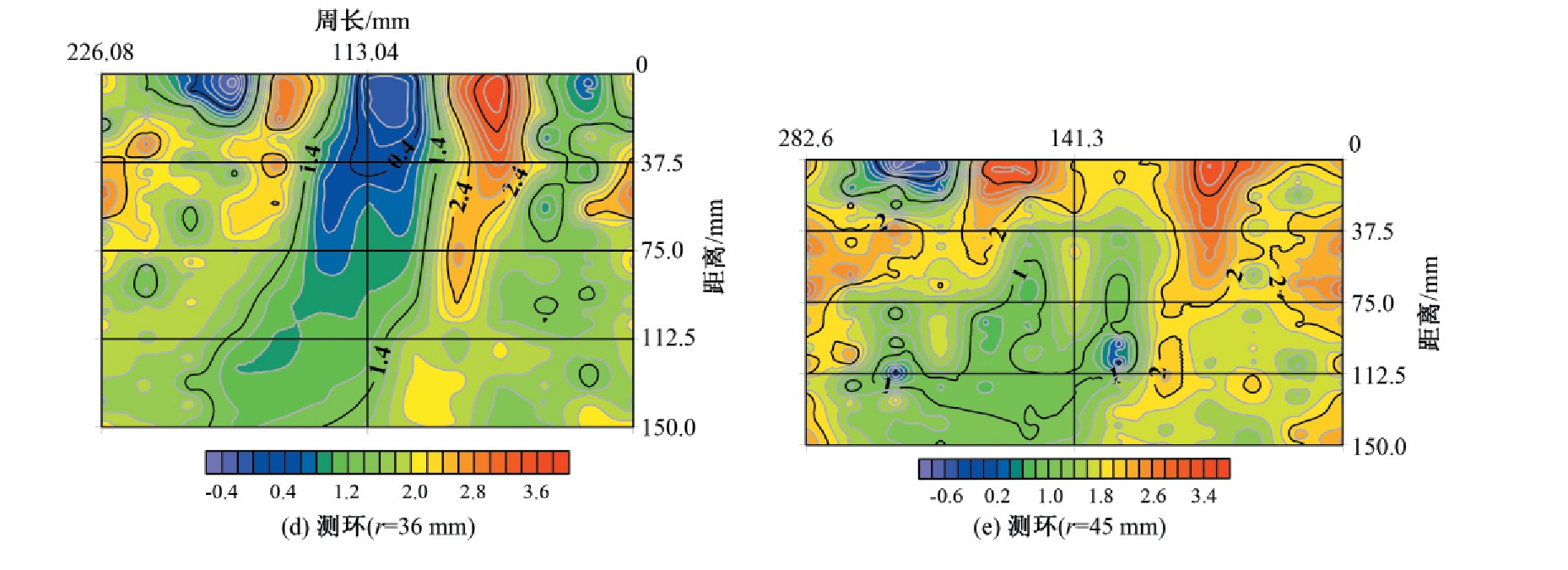
　　Fig.5 Axial velocity distribution on the side of the same measuring ring

　　2.3、 典型测点轴向速度分析

　　对不同测环下上典型测点上轴向速度沿横截面变化进行分析,选取9、18、27、36、45 mm半径的5个测环上对应0°、60°、120°、180°、240°、300°角度上的测点为例。具体见图6。(60°,9 mm)便是极径为9 mm测环上60°极角下的测点,其余测点以此类推。

　　图6 不同典型测点轴向速度沿横截面变化曲线

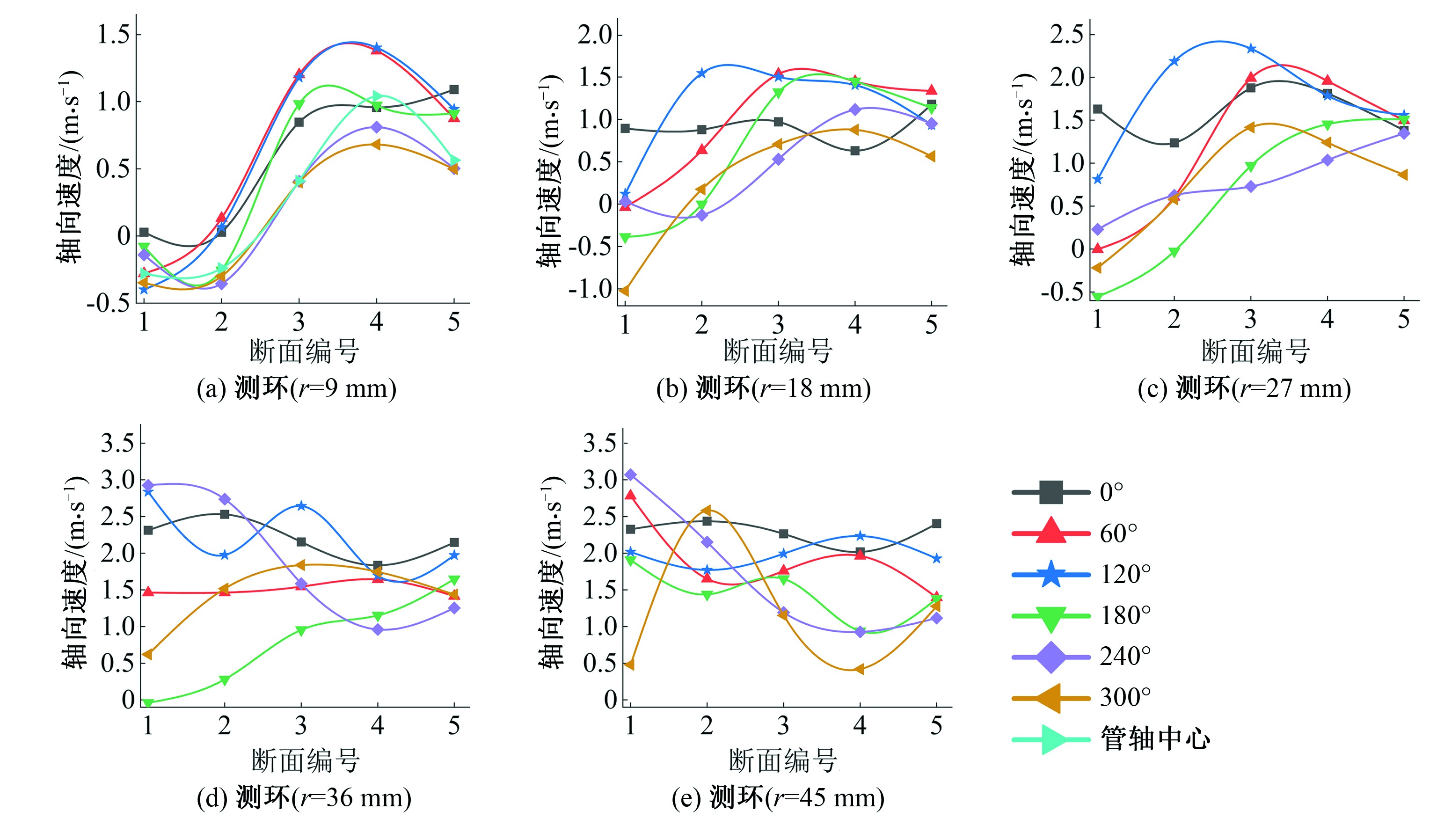
　　Fig.6 Variation curves of axial velocity along the cross section of different typical measuring points

　　从图6中可以看出:

　　(1)随着测环直径的增大,整体上各测环沿程横截面上典型测点轴向速度是先扩散后聚拢的走势,紧贴后圆柱体断面典型测点轴向速度值极差最大,紧贴前圆柱体断面典型测点轴向速度极差最小。

　　(2)紧贴后圆柱体横截面轴向速度值大多为负值,速度方向为逆水流方向,随着横截面的增加,负值情况减少,该影响范围集中于半径为36 mm以内。这是由于水流沿后圆柱体导流条及支撑体流动至测试范围内,无圆柱体及配件的阻挡,过流面积骤然增大,形成漩涡,使得水流减速至负方向。

　　(3)紧贴后圆柱体横截面各典型测点轴向速度变化梯度最大,轴向速度分配不均匀。紧贴前圆柱体横截面上各典型测点轴向速度值极差小,数值波动小,轴向流速收敛。紧贴前圆柱体支撑体的截面,受前圆柱体阻挡影响,过流面积骤然缩小,水流受阻。

　　(4)相同测环不同测点轴向速度沿横截面变化曲线中,基本成两组分化状态,极角为0°、120°、240°的测轴上测点轴向速度普遍大于极角为60°、180°、330°测环上测点的轴向速度。这是由于极角为0°、120°、240°的测轴位于两支撑体中间位置,在后圆柱体导叶下游,受后圆柱体导叶导流作用,轴向速度较大。

　　(5)半径为9 mm测环上各测点轴向速度沿横截面变化曲线与圆心上轴向速度沿横截面变化曲线的走势较吻合,半径9 mm测环内沿横截面的圆柱状区域与测环a外水流流体撞击影响小,轴向速度与水流其他能量交换变化整体平缓。

　　3、 结 论

　　本文通过对圆柱体间轴向流速分布规律进行研究,对比分析了不同横截面、测环、典型测点的轴向速度,得出以下结论:

　　(1)对于沿水流方向距离原点不同距离横截面的水流轴向速度分布,圆柱体间轴向速度分布呈现旋转对称-轴向速度分布均匀化-趋向旋转对称的发展规律。

　　(2)对于圆柱状测量范围内不同直径的测环圆柱体间轴向流速分布,下游水流受后圆柱体导流条引流产生周向速度,流速分布因能量的相互传递进行重新分配,使得整体柱状测量范围轴向流速上下左右均呈现不对称情况;测试范围内下游部分水流在上游导流条引流作用下轴向流速分布逐渐整体偏离管轴中心线。

　　(3)水流沿后圆柱体导流条及支撑体流动至测试范围内,无圆柱体阻挡,过流面积骤然增大,受旋转对称支撑体影响,形成漩涡,使得水流减速至负方向,紧贴后圆柱体支撑体横截面中轴向速度出现负值。

　　参考文献

　　[1] 李永业,孙西欢,李飞,等.动边界同心环状缝隙流研究[J].农业机械学报,2012,43(3):230-234.
　　[2] 张琪琦,孙西欢,李永业.圆柱体绕流环隙流场轴向流速及水力损失试验研究[J].长江科学院院报,2015,32(4):51-54,58.
　　[3] 吴剑,孙西欢,李永业.不同直径圆柱体同心环状缝隙流轴向速度特性研究[J].中国农村水利水电,2017(12):185-188.
　　[4] 吴新,邹志风.旋转方式对并列双圆柱绕流特性的影响[J].人民黄河,2017,39(11):71-75.
　　[5] 邹帅,徐加辉,周杰,等.过渡流下钝体绕流特性的可视化实验对比[J].化工学报,2016,67(S1):210-216.
　　[6] 刘志荣,邹赫,刘锦生,等.开缝圆柱缝隙倾斜角对脱落涡的影响[J].北京航空航天大学学报,2017,43(1):128-135.
　　[7] 周潇,胡烨,王晋军.前置隔板对圆柱绕流影响的实验分析[J].北京航空航天大学学报,2016,42(1):172-179.
　　[8] 张宾,唐湛棋,孙姣,等.旋转圆柱绕流的动力模态分析[J].河北工业大学学报,2015,44(4):63-67.
　　[9] 杜晓庆,林伟群,施春林,等.高雷诺数下并列双圆柱绕流的大涡模拟[J].哈尔滨工业大学学报,2019,51(6):193-200.
　　[10] 王伟,宋保维,毛昭勇,等.脊状结构表面圆柱绕流的流体特性研究[J].华中科技大学学报(自然科学版),2018,46(,9):107-111,132.
　　[11] 龚志军,杨佼,武文斐,等.并列双柱绕流的格子Boltzmann模拟[J].水电能源科学,2013,31(11):117-120.
　　[12] CANUTO D,TAIRA K.Two-dimensional compressible viscous flow around a circular cylinder[J].Journal of Fluid Mechanics,2015,785:349-371.
　　[13] GAO W,NELIAS D,LIU Z,et al.Numerical investigation of flow around one finite circular cylinder with two free ends[J].Ocean Engineering,2018,156:37.