摘要:中小学教学衔接问题一直以来备受关注,发挥评价的诊断和导向功能是解决该问题的新尝试。以北京市某区初一年级数学前测为例,探讨如何制定测试的内容框架和能力框架,呈现部分试题,并从学科能力的角度进行分析。据此提出初一前测命题应符合课程标准、应服务于考查目标、应体现诊断功能等建议。
关键词:教学衔接; 数学命题; 前测; 学科能力;
A Study on the Item Development of Mathematics Pretest in Grade Seven to Promote the Connection of Mathematics Teaching in Primary and Secondary Schools
BAI Yongxiao CAO Chen
Beijing Normal University Beijing Institute of Education
Abstract:The problem of teaching linkup between primary and secondary schools has always attracted much attention, and it is a new attempt to solve this problem to give full play to the diagnostic and guiding functions of evaluation. Taking a mathematics pretest of grade seven in a certain district of Beijing as an example, this paper discusses how to develop the content framework and competency framework of the test, presents some test items,and analyses them from the perspective of subject competencies. Accordingly, it is suggested that the item development of pretest for grade seven should conform to the curriculum standards, serve the examination objectives, and embody the diagnostic function.
中小衔接,一般是指义务教育阶段小学与初中的衔接,特指六年级与初一年级的衔接。多年以来,中小衔接问题一直是数学教育上的一个难题,主要表现在小学生升入初中后对数学学习产生的陌生感和落差感,中学教师把学生不适应的情况归因于小学教学没有为学生的中学学习做好铺垫。课程改革之前中学和小学分别设有独立学段的大纲,之后的新课标教材呈现一纲多本,目前小学和初中独立建校的情况仍占多数,特别是一线中小学教师互不了解彼此的教学内容及教学情况,以上这些因素都对中小学数学衔接造成很大的困难。我国2012年颁布的《全日制义务教育数学课程标准(2011年版)》(以下简称《课程标准(2011年版)》),体现了义务教育阶段数学课程的整体性,在通盘考虑9年课程内容的基础上划分为3个学段,在各个学段安排4个学习领域的内容,从结构设置上加强小学和初中数学的联系,有利于更好地完成义务教育阶段的任务和目标,消除之前造成不衔接的部分因素;但是,由于中小衔接问题的长期性和复杂性,衔接问题仍未得到解决。
近年,国内学者对中小衔接问题的原因和对策进行了研究。有研究者认为初一新生不适应初中数学学习主要存在以下原因:小学数学的基础知识和技能不扎实,学生对教师的教学方法不适应,学生的学习方法不适应初中阶段学习,学生的思维方式和水平跟不上初中数学学习[1]。关于中小衔接问题解决对策的研究结论比较一致,提出要关注数学教材知识的衔接、数学教师教学衔接、学生数学学习的衔接,且普遍认为重点是学生数学学习的衔接,重中之重是做好学生的数学思维和能力的衔接。另有研究指出,中小学衔接方面存在的问题之一是“重理论不重实际,对思维发展的现状定位不准”,认为现在的儿童思维发展水平已经超出之前的皮亚杰研究定论,因此,有必要在小学阶段更加关注学生的数学思维训练和发展[2]。以往研究多是从教材内容、教师教学和学生学习的角度提出解决中小衔接问题的方法和建议,特别是提出学生数学思维的衔接是解决问题的关键,在教学中应多加关注,但是从评价命题的角度探讨中小衔接问题的研究尚不多见。
教学、学习和评价是一个不可分割的整体,评价具有导向功能,影响教的行为、学的行为和教育管理者的行为。从评价结果的应用来看,评价以促进学生学习为根本目的,将评价结果得到的信息作为改进教学的依据[3]。因此,发挥评价的导向与诊断功能,对促进中小衔接具有重要的意义:一方面促使小学教师的教学能够更好地为初中学习做准备,另一方面也有助于中学教师在了解初一年级新生现有基础后进行有针对性的教学。从实践层面看,一些地区已开展了初一年级新生的前测工作,着重对初中、小学都涉及的学习内容以及必要的能力进行了考查。从评价类型看,初一年级前测属于配置性测评,回答了“学生在多大程度上具备后续学习所需的知识与能力”的问题[4]。笔者参与了北京市F区初一年级前测的命题和反馈工作,本文将以此为例,对基于中小衔接的初一年级数学前测如何开展才能考查学生必备的数学能力进行探讨。
1 测试框架
初一年级前测既可以考查学生基础知识的掌握情况,又能够考查学生所具备的数学能力,因此包括内容和能力2个维度。
1.1 内容维度
初一年级前测的内容基本需要覆盖《课程标准(2011年版)》第二学段中的二级内容项目:数的认识、数的运算、式与方程、正比例与反比例、探索规律、图形的认识、测量、图形的运动、图形与位置、简单数据统计过程、随机现象发生的可能性等,由此体现《课程标准(2011年版)》对六年级毕业生的基本要求。
“数与代数”一直是小学和初中学习的重点和难点内容,因此在中小衔接测试中可以适当加大“数与代数”内容的考查比例。在F区中小衔接测试中,数与代数、图形与几何、统计与概率3大内容领域的分值比率约为7∶2∶1(见表1)。
表1 北京市F区初一前测试题的内容分布
1.2 能力维度
为了进一步区分学生的数学能力,命题借助“3×3数学学科能力框架”[5],对《课程标准(2011年版)》中“了解、理解、掌握、运用”4个结果性目标进行细化。该框架将数学学科能力分为学习理解、应用实践、迁移创新3个水平,每个水平再细分为3个要素,具体能力要素内涵界定如表2所示;同时,该框架也在一定程度上考查了学生的数学核心素养。
F区初一前测以“3×3数学学科能力框架”作为能力维度的框架,考查学生在各个能力层次的表现,试题的能力分布见表3。
在A1至B3的基础能力中,重点考查学生在“计算与操作(A2)”层级的表现,旨在了解学生对于基础技能的掌握情况;对于“解释与交流(A3)”和“分析与概括(B1)”2个能力层级的考查,旨在判断学生对数学知识的理解程度,是否具备了进一步学习的基本能力;对于学生的知识应用能力,则通过“简单问题解决(B3)”层级的考查予以实现。
除考查以上基础知识和基本能力之外,促进中小衔接的前测还需要评价对初中学习起着关键作用的高层次数学能力。F区前测还对“综合应用(C1)”“猜想与发现(C2)”和“探究与建模(C3)”3个高层级能力进行了考查,其结果可以为初中教师将开展的教学工作提供参考,同时也可以反映出该区小学教学中是否关注了学生高层次能力的发展。
2 测试题目与分析
在制定测试框架、编制命题细目表之后,最重要的环节就是试题的命制。以下呈现F区初一年级前测中的部分试题,并从学科能力的角度作出分析。
2.1 考查“解释与交流”维度的试题
“解释与交流”维度主要考查学生能否利用数学对象对具体情境中的现象进行解释,能否通过举例或者画图的方式解释数学对象,即考查学生对数学概念和数学技能是否理解。1976年,Skemp首次提出关系性理解和工具性理解的概念,讨论了关系性理解(知道如何做某事和为什么做某事)和工具性理解(知道法则但不知道理由)之间的区别。Skemp认为,尽管基于工具性理解教学更容易、更直接,能更快地得到答案,但是基于关系性理解的教学更有价值,因为它能够使学生适应新任务,促进学生数学能力的发展[6]。《课程标准(2011年版)》也指出,教师既要关注数学学习的结果,也要关注数学学习的过程,从而帮助学生在知识与技能之间保持平衡。
表2 3×3数学学科能力框架[5]

表3 北京市F区初一前测试题的数学能力分布
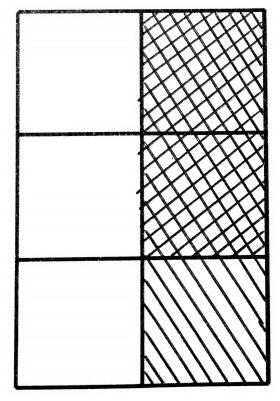
例1(测试卷第23题)画图表示
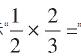
的过程和结果.
就运算而言,很多学生处于“知其然而不知其所以然”的状态,缺乏对算理的认识。例1主要考查学生能否理解分数乘法的本质意义,并通过直观的方式进行呈现。与之相应,对于乘法公式运算过程的考查也是初中代数学习的重点和难点。
图1是例1的正确答案,学生首先需要将6块方格中的3块打上斜纹,体现出对“”的认识;其次学生需要将3块斜纹方块中的2块标记出来,体现出对“的”的认识。学生只有具备了通过合理的方式描述运算过程的能力,才说明学生达到了“解释与交流”的水平。此外,该题也考查了学生的直观素养。
图1
2.2 考查“简单问题解决”维度的试题
许多数学教育专家对于学生在文字应用题中的表现进行了系列研究,一致认为,文字应用题是学生在学习代数过程中需要面临的挑战。在文字应用题中最大的困难是学生需要将“故事”转化为正确的代数式。Bishop提出,自然语言与代数语言之间的相互转化是学生在中小衔接阶段面临的三大困难之一[7]。
例2(测试卷第27题)从2016年1月1日开始,某市居民生活用气阶梯价格制度正式实施,一般生活用气收费标准如下表所示.
某市居民用气价格方案

小强家2017年全年使用天然气510 m3,需要交多少元?
Van de Walle指出,变化率问题有着广泛的应用,因为它涉及很多学生熟悉的情境,如速度、油耗、利润和支出等[8]。如果使用学生熟悉的情境呈现函数,小学生也可以对函数进行有意义的学习,如四年级的学生就可以分析植物高度随时间变化的生长状况。
阶梯价格是学生非常熟悉的生活情境,可以用于了解学生的模型素养。在该题中,学生首先需要阅读表格信息,结合小强家2017年全年用气量,判断出小强家的用气量属于“第三阶梯”;再根据试题背景信息,正确理解“阶梯价格”的实际含义,否则有可能在计算费用时将价格全定位于4.0元/m3;最后列出算术表达式,得到答案。本题的重点和难点出现在对表格信息的理解上,只有正确理解了问题的实际情境并顺利地解决问题,学生才能达到“简单问题解决”的能力层级。
2.3 考查“综合应用”维度的试题
“综合应用”维度主要考查学生能否具有解决由多个知识点构成的纯数学问题的能力。为了更好地体现“字母表示数”在中小衔接数学学习中的重要意义,为初中的代数学习做好准备,在F区的测试中突出了对学生代数思维的考查。
例3(测试卷第10题)数轴上,两点的位置如下图所示,下列说法正确的是___.
学生在小学阶段对于“字母可以表示任何数”已经有了初步的认识,再加上学生已经学过“数线”的知识,可以通过“数线”估计数的大小,因此学生具备解决该问题的知识基础。Darley指出:“只有当学生对数,以及数和字母之间的联系产生了深刻的理解,他们才能够顺利地实现数与字母之间的相互转化。”[9]在该题中,学生需要掌握以下3点:一是理解数线上字母a、b的意义;二是根据数线,对a、b的大小进行估计;三是理解代数式、ab的意义,大致判断它们的大小。学生只有正确地解决以上问题,才能达到“综合应用”的能力层级。
2.4 考查“探究与建模”维度的试题
“探究与建模”是“3×3数学学科能力框架”的最高层级。在该层级中,学生需要用所学的新知识探究解决新问题的方法。独立思考、学会思考是探究的核心,归纳概括得到猜想和规律并加以验证是探究的重要方法。探究是初中阶段学生学习数学的重要途径,应得到充分的重视。
例4(测试卷第28题)古埃及人在进行分数运算时,只使用分子是1的数,因此分子为1的分数也被称为埃及分数.我们注意到,某些埃及分数恰好可以表示为两个埃及分数的差,例如
(1)请按这样的规律再写出一个埃及分数,并表示为两个连续埃及分数的差;
(2)能这样表示的埃及分数有很多,请用适当的方式表示出这个规律;
(3)结合上面的发现,计算出的值.
在设计考查学生探究能力的问题时,命题往往需要由浅入深,注意难度梯度;通过子问题的设置,给学生足够的提示,搭好解决问题的“脚手架”。例4分为3个问题,在题干中,通过举例的方式让学生认识某些埃及分数的特征。第(1)问考查了“分析与概括(B1)”能力,学生需要分析给定等式两边的结构,归纳出共同的特征,再写出一个类似的含有埃及分数且满足给定条件的等式,能够正确回答则说明学生达到了B1水平。第(2)问考查了“猜想与发现(C2)”能力,从第(1)问的初步认识规律并举出例子,到通过归纳发现规律并正确地表示出来,是能力层次的提升。第(2)问的答案并不唯一,发现的规律用文字叙述、字母表达均可;能正确回答出第(2)问说明学生已经具备在新的情境下猜想探究出新知识、发现数学的模式或规则的能力,达到了C2水平。第(3)问考查了“探究与建模(C3)”能力,这是一个较为复杂的分数计算问题,如果学生能将在第(2)问中发现的规律在第(3)问中进行应用,说明学生已经具备了能用所学的新知识探究解决新问题的能力,即达到了C3水平。在该题中,从发现规律、表达规律到应用规律,环环相扣,适合于考查学生的高层次思维。通过对该问题的解决,可以使学生通过深入的数学思考,获得解决数学问题的策略,积累数学探究的经验。
3 结论与启示
在初一年级数学前测命题工作中,不但要考查学生所具备的基础知识和基本技能,更需要考查学生的数学能力。为实现这些目标,需要关注以下3个方面。
首先,命题应符合课程标准。《课程标准(2011年版)》是义务教育数学教材编写和教学实施的指导性文件,同时也是初一年级前测命题的基本依据。命题应符合课程标准的精神,考查的内容基于《课程标准(2011年版)》中第二学段的内容,考查初一年级新生的核心知识和能力。特别需要指出的是,命题应体现正确的价值取向,不适宜出现小学奥数的试题。
其次,命题应服务于考查目的。初一年级前测考查对象是从小学刚刚升入初中的学生,主要目的是考查学生进入初一年级的“预备状态”,了解学生是否具备了初中学习所需要的必备知识和能力,发现学生哪些内容掌握得较好,哪些内容还存在困难,为初中教师进行针对性教学提供依据,更好地促进中小学衔接。在命题中,既要体现出初中生数学学习需要具备的重点知识和重要技能,如数的运算、字母表示数等内容以及运算技能和合情推理等能力,又要保证有一定比例的较难试题,用以考查学生较高层次的能力,以解决中小衔接主要反映在小学生数学思维能力不能适应中学学习的问题,如考查对于中学数学学习很重要的“解释与交流(A3)”“推理与论证(B2)”“猜想与发现(C2)”“探究与建模(C3)”等能力。
最后,命题应体现诊断功能。本次测试采用“3×3数学学科能力框架”,对《课程标准(2011年版)》中用“了解、理解、掌握、运用”等术语表述学习活动结果目标的不同水平进行了细化,并进行了相应的描述,能够更为精确地考查不同学生的数学能力及学习特点。小学教师根据测试反馈,可以有目标、针对性地改进自己的教学;中学教师根据测试反馈,可以准确地了解初一年级学生整体及个体的学习起点与特点,采取措施提前对学生的中学数学学习进行规划和调整。因此,基于学科能力框架的初一年级前测命题工作在某种程度上能够为中小学数学教学衔接问题的解决提供参考。
参考文献
[1]王永春.小学数学与初中数学衔接问题的思考[J].课程·教材·教法, 2009(7):42-46.
[2]宋鸿梨.中小学数学的衔接研究:从思维发展的视角[D].武汉:华中师范大学, 2011.
[3] WILLIAM D. What is assessment for learning?[J]. Studies in Educational Evaluation, 2011, 37(1):3-14.
[4] 格朗伦德.学业成就测评[M].杨涛,边玉芳,译.南京:江苏教育出版社, 2008:3.
[5]綦春霞,何声清.基于“智慧学伴”的数学学科能力诊断及提升研究[J].中国电化教育, 2019(1):43.
[6] SKEMP R R. Relational Understanding and Instrumental Understanding[J]. The Arithmetic Teacher, 1978, 26(3):9-15.
[7] BISHOP A, FILLOY E, PUIG L. Educational Algebra:A Theoretical and Empirical Approach[M]. Boston:Springer, 2008.
[8] VAN DE WALLE J A, KARP K S, BAY-WILLIAMS J M. Elementary and Middle School Mathematics:Teaching Developmentally[M]. 7th ed. New York:Pearson Education, 2010.
[9] DARLEY J. Traveling from Arithmetic to Algebra[J]. Mathematics Teaching in the Middle School, 2009, 14(8):458-464.



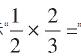 的过程和结果.
的过程和结果.