摘 要: 数学符号意识是我国义务教育阶段学生的一种数学核心素养, 在国际数学教育中, 各国也非常重视学生数学符号意识的培养。通过测评, 得出以下结论:义务教育阶段学生数学符号意识发展水平随着年级的增长不断升高, 具体可以划分为四个发展水平, 即经验观察水平、本质内化水平、理性辩证水平、结构普适水平, 并在四个分析层次上逐渐分布均衡。
关键词: 义务教育阶段; 数学符号意识; 分析层次; 发展水平;

Abstract: Developing students'key competency not only aroused the worldwide re-examination of the curriculum reform, but also attracted the attention of the construction and evaluation of the discipline key competency.The mathematical symbol sense is a kind of key competency of math in compulsory education, and it obtains great attention in the international community.By investigation, this paper drew the following conclusions:the development of students'mathematical symbols can be divided into four levels, that is, the experience observation level, the nature internalization level, the rational dialectical level and the universal structure level.The development level in compulsory education is increasing with the growth of the grade and gradually balanced in the distribution of the four levels.
Keyword: compulsory education; the mathematical symbol sense; analysis level; level of development;
一、问题提出
罗素 (Russell) 在《西方哲学史》中写道:“数学的真理, 正如柏拉图所说, 乃是与知觉无关的;它是非常奇特的一种真理, 并且仅只涉及符号。”[1]虽然这样的描述忽视了直观经验在数学符号形成过程中的重要作用, 但是从另一个方面我们可以看出, 数学符号对数学或者是数学真理的影响是巨大的。可以说, 整个数学的发展历史就是数学符号产生与完善的历史。数学课程任务之一就是让学生感悟和拥有使用数学符号的能力。因此, 一些国家 (如芬兰、新加坡、加拿大、美国、德国、英国等) 把发展学生的“符号意识”作为数学教育的一个重要目标写入课程标准。
目前, 国内外对数学符号意识的研究主要集中在内涵界定、要素构成与如何培养三个方面。关于数学符号意识内涵界定的研究可以归纳为两种形式。第一种主要是由意识的概念出发, 形成“意识+数学教育术语”式的定义。这种内涵的界定在一定程度上强调了数学符号意识中的“意识”层面, 注重人的能动性, 体现了人对数学符号运用、交流和理解的主动自觉性。[2-3]第二种主要是由数学符号出发, 形成“符号+数学教育术语”式的定义。这种内涵界定关注数学学科特征, 更侧重对数学符号的描述, 将数学符号意识视为数学符号语言的一种表征形式。[4-5]关于数学符号意识要素构成的研究主要集中于四个取向, [7-10]即能力取向、心理取向、行为取向、多重取向, 所提及的关于数学符号意识维度的划分主要是根据研究者各自的研究经验或者是相关理论, 也有在一定程度上的验证。随着数学核心素养的提出, 有必要对作为数学核心素养之一的数学符号意识的构成要素作出适时调整。关于数学符号意识培养的研究, 主要集中在四个方面:第一, 在数学符号意识培养过程中注重引入数学符号的必要性;第二, 在数学符号意识培养过程中注重不同数学符号 (字母、图形、关系式) 之间的相互转换;第三, 在数学符号意识培养过程中注重学生已有经验基础与心理特征;第四, 在数学符号意识培养过程中注重培养学生对数学符号的意义与本质的理解。[11-14]
学生的义务教育具有连贯性, 在我国, 习惯性地将义务教育分为小学教育 (一年级至六年级) 和初中教育 (七年级至九年级) 两个阶段, 从学生受教育的整体来看, 这样的划分是满足学生认知发展规律与心理特征的, 但是这种划分并非针对某一学科、某一领域而言。当我们将研究问题放入具体学科中的某一内容, 再以这样的划分方式进行研究, 就有失妥当。在一些研究中, 往往是分别对小学或者初中的学生数学符号意识进行研究, 从而使所得研究结果呈现间断性、局限性与片面性。单独关注小学或者初中阶段的数学符号意识研究是不够的, 不同年龄的学生在不同阶段的数学符号意识的水平的划分, 直接影响数学符号意识培养策略的选择与制定。因此, 从整个义务教育阶段出发, 研究学生数学符号意识发展水平是非常必要的。根据以上分析, 本研究基于实证调查具体研究以下三个问题: (1) 学生数学符号意识的整体状况如何; (2) 学生数学符号意识的关键节点在哪里; (3) 学生数学符号意识可以划分为几个发展水平。
二、研究方法
(一) 研究对象的选取
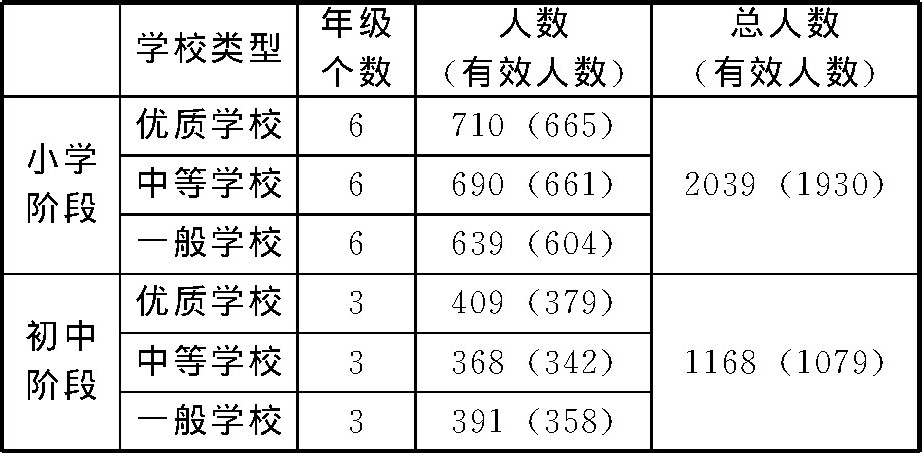
本研究选取了综合发展水平处于中等的三个城市中的义务教育阶段的学生作为研究对象。研究采取分层抽样和整群抽样相结合的方法, 首先根据学校的生源质量、管理水平、课程设置、师资力量等, 将学校分成优质学校、中等学校、一般学校三个层次水平, 然后分别在不同层次水平的学校中各随机选取三所学校作为样本学校, 在被确定为样本学校的每个年级中选取一个普通班级的学生作为样本。共发放测试卷3207份, 其中小学2039份, 初中1168份, 研究对象的具体分布如表1所示。
表1 研究对象的分布
(二) 测试卷的编制
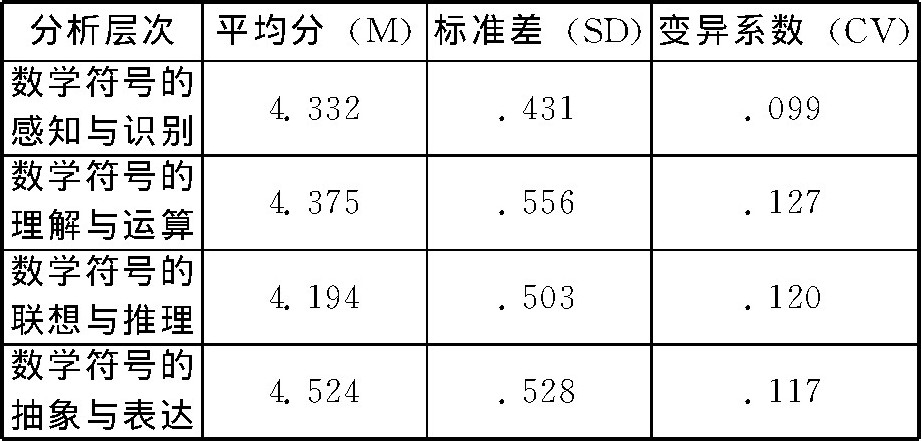
费 (J.Fey) 曾指出数学符号意识包括认知与鉴别技能、估算技能、验算与预测技能、选择技能。[4]阿卡维 (Abraham Arcavi) 认为数学符号意识包括理解并应用符号去表达隐性的数量关系、一般化以及证明、知道数学符号的取舍、数学符号的操作和解读、符号之间的转换关系、数学符号的选择与替换、数学符号意义的解释。[15]《义务教育数学课程标准 (2011年版) 》 (以下简称《标准 (2011年版) 》) 中指出:符号意识是理解并运用数学符号表示数、数量关系和变化规律;知道使用符号可以进行运算和推理, 得到结论具有一般性, 建立数学符号意识有助于学生数学表达与数学思考。[16]还有很多研究者也提出各自的数学符号意识的维度。[17][3][18][14][6]综合已有研究, 笔者对数学符号意识关键词进行提炼, 编制五级量表, 利用德尔菲法, 通过对数学教育理论研究者、数学教研员、数学教师进行三轮专家咨询 (如表2所示) 。从集中程度来看, 四个分析层次的平均分在4.194分至4.524分之间, 均高于3.75 (5分量表的百分之七十五等级值) ;从离散程度看, 各数学符号意识分析层次的标准差在0.431至0.556之间, 所有分析层次的标准差均小于1, 说明专家意见相对比较集中;每个分析层次的变异系数在0.099至0.127之间 (数值均较小) , 反映了本研究中所选取的专家群体对于数学符号意识分析层次的测评协调程度较高。因此, 我们得出数学符号意识的四个分析层次:数学符号的感知与识别、数学符号的理解与运算、数学符号的联想与推理、数学符号的抽象与表达。
表2 数学符号意识分析层次专家咨询结果
事实上, 当我们在预测一个试题难度的时候, 往往会发现, 试题除了有客观难度以外, 还有主观难度, 并且与许多因素相关, 包括试题所要求的知识与思维的复杂程度, 试题所创设问题情境的新颖性, 试题的类型, 试题对学生的考查价值, 等等。[19]基于此, 本研究中测评题项的设计主要从以下两个方面考虑:一是学生符号意识分析层次的划分, 二是学生数学符号意识的发展阶段。前者主要决定了测评题项的内容与广度, 后者主要决定了测评题项的类型与深度。为尽量满足学生的认知发展规律, 考虑到题目的层次性, 在测试卷中既安排了基础性的题目, 也安排了发展性的题目。鉴于对整个义务教育阶段学生数学符号意识进行测量, 测试卷将按照学段编制, 每个学段形成一套测试卷, 同时为了更好地消除“一致”和“差异”之间的矛盾, 三套测试卷之间采用四道锚题连接, 其作用在于降低随着年级的升高学生的学习能力所带来的影响。
(三) 测试卷的信度与效度
本研究中测试卷的信度如表3所示, 从表中可以看出, 各分测评的CronbachAlpha值在0.807至0.903之间, 均大于0.800, 表明分测评信度很高;测试卷总体CronbachAlpha值在0.854至0.910之间, 均大于0.800, SpearmanBrown系数在0.833至0.901之间, 均大于0.800, 表明各学段测试卷整体信度很高, 通过信度检验, 测试卷的α信度指标基本达到了测量学要求, 各分测评之间具有很高的一致性, 适宜作为测量工具使用。
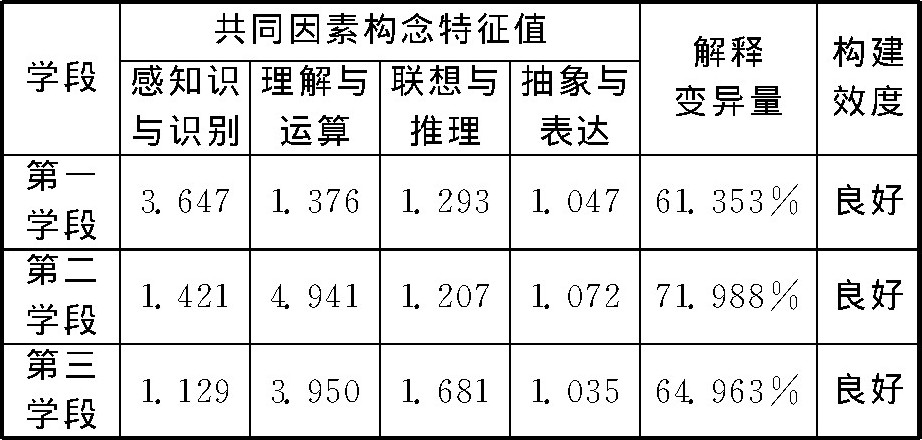
本研究采用主成分分析萃取法, 共抽取四个共同因素 (如表4所示) , 从表中可以看出各学段四个因素构念联合解释变异量均大于60%, 因素负荷量情况较好, 旋转后的因素负荷矩阵和累积解释变异量表明, 提取的四个因素对整个测试卷的有效程度较好, 四个分析层次的结构具有很好的稳定性和独立性, 测试卷的内部结构较为理想, 保留萃取的四个因素其建构效度较好, 形成三个学段学生数学符号意识的测试卷。
表3 各学段测试卷信度表
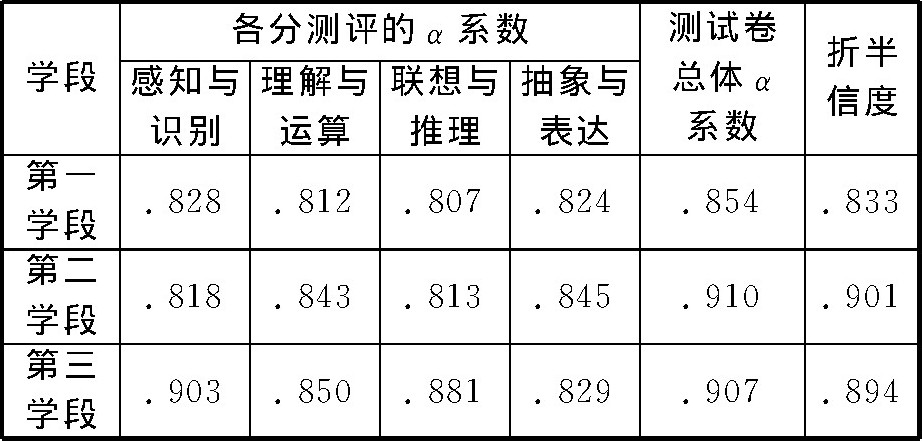
表4 各学段测评问卷建构效度表
我们利用Pearson相关分析来检验各分析层次之间是否存在相关性 (如表5所示) 。通过相关性分析可以看出, 各分析层次与总测试卷存在显着相关。
表5 各分析层次间的相关系数矩阵
(四) 施测与评分
本研究采用团体测评的方法, 由研究者与被试学校教师组织施测, 研究对象完成测试卷的时间为45分钟。研究者与两名数学教师共同制定评分标准与细则。为了避免单一评分者所造成的测量偏差, 本研究对于测试卷的评分由两名硕士研究生依据评分标准和细则独立完成, 对于不一致的评分由研究者仲裁, 两名硕士研究生的评分一致性程度很高, 达到了95%以上的评分一致。
三、研究结果
(一) 学生数学符号意识的整体表现
在对义务教育阶段学生数学符号意识的发展水平进行划分之前, 笔者提出这样的假设: (1) 学生数学符号意识发展水平会受到年龄因素的影响, 具体表现在本研究中就是义务教育阶段年级的变化, 教师教学、课外辅导等其他信息接收途径不在本研究考虑范围之内; (2) 学生数学符号意识的发展水平可以通过学生数学符号意识测试卷的总平均分来反映, 同时还受到数学符号意识各分析层次的测评状况的影响。
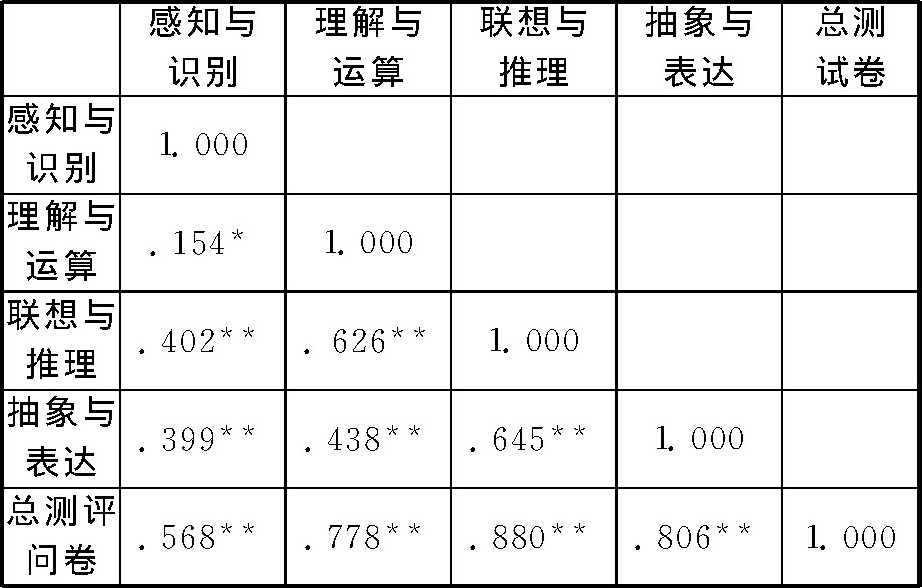
基于以上两个假设, 以18所学校 (9所小学、9所初中) 学生的数学符号意识测评分数作为分析对象, 期望能够从整体上对各年级的测评情况有一个了解与把握。首先通过折线统计图直观地了解一下学生数学符号意识随年级的变化情况。如图1所示, 各年级学生数学符号意识测试卷总平均分的得分情况为:一年级总平均分为9.400分 (1) , 二年级总平均分为10.064分, 三年级总平均分为13.648分, 四年级总平均分为13.837分, 五年级总平均分为15.698分, 六年级总平均分为16.134分, 七年级总平均分为16.492分, 八年级总平均分为21.096分, 九年级总平均分为21.511分。一年级至四年级学生平均分低于14.4分 (总分的60%) , 五年级至七年级学生平均分高于14.4分, 八、九年级学生平均分高于19.2分 (总分的80%) 。从学生数学符号意识发展曲线我们可以看出, 义务教育阶段各年级学生数学符号意识总平均分出现了两次大幅度上升, 一次是二年级至三年级, 总平均分升高了3.584分 (从10.064分至13.648分) , 另一次是从七年级至八年级, 总平均分升高了4.604分 (从16.492分至21.096分) 。
下面笔者根据测试卷的结构, 进一步检验义务教育阶段各年级学生在数学符号意识四个分析层次即数学符号感知与识别 (GS) 、数学符号理解与运算 (LY) 、数学符号联想与推理 (LT) 、数学符号抽象与表达 (CB) 的平均分与得分比例的变化情况。
图1 学生数学符号意识总平均分变化趋势
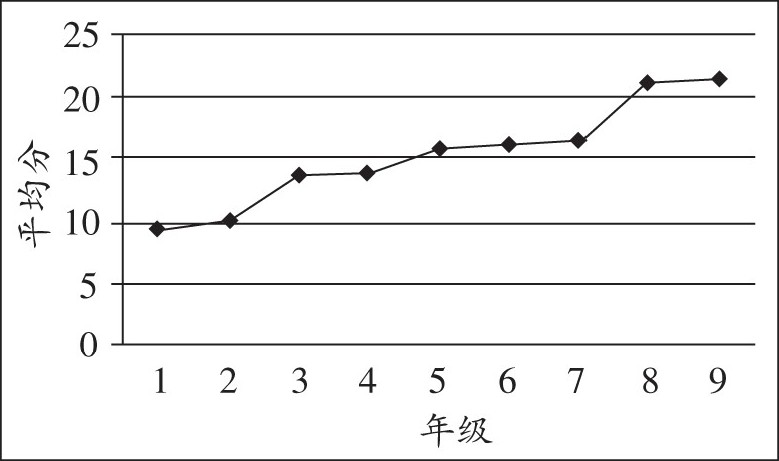
图2 各年级在四个分析层次平均分变化趋势
从各年级学生在数学符号意识四个分析层次平均分变化趋势来看, 图2中九条曲线分别表示一年级至九年级学生在数学符号意识四个分析层次平均分的变化情况。学生在各分析层次的平均分随着分析层次要求的升高逐渐降低, 这是正常的, 九个年级学生都是在GS分析层次的平均分最高, GS分析层次是数学符号意识最低层次, 是其他层次的基础。在CB分析层次的平均分最低, CB分析层次是数学符号意识的最高层次。对于同一个分析层次而言, 学生在每个分析层次的平均分随着年级的增长而升高。从图中可以看出, 数学符号意识整体上可以分为四个集合:一、二年级学生的数学符号意识发展水平接近, 可以将其视为一个集合;三、四年级学生的数学符号意识发展水平接近, 可以将其视为一个集合;五、六、七年级学生的数学符号意识发展水平接近, 可以将其视为一个集合;八、九年级学生的数学符号意识发展水平接近, 可以将其视为一个集合。
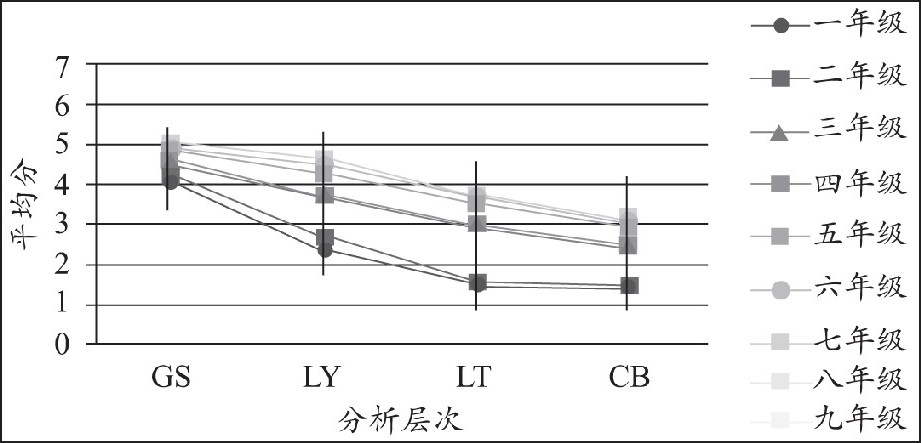
从各年级学生在数学符号意识四个分析层次的得分比例来看 (如图3所示) , 在四个分析层次中, 一年级在GS分析层次得分比例最高 (43%) , 接近50%, 虽然随着年级的增长, 感知与识别层次的得分比例逐渐降低, 但是九年级感知与识别层次的得分比例 (27%) 也达到25%;各年级在LY分析层次的得分比例均达到25%, 其中一年级的得分比例 (25%) 最低, 六年级与七年级得分比例 (28%) 最高;各年级在LT、CB两个分析层次得分比例均未达到25%, 其中一、二年级在LT分析层次得分比例仅为16%, 在CB分析层次得分比例仅为15%, 九年级在LT分析层次得分比例 (24%) 接近25%, 在CB分析层次得分比例 (22%) 也不是很高。八年级与九年级在四个分析层次上的得分比例大体上呈现出均衡分布。从四个分析层次在测试卷结构中的得分比例来看, 低年级 (一、二年级) 在GS、LY、LT、CB四个分析层次的得分比例非常不均衡, 随着年级的升高, 学生在四个分析层次的得分比例差距逐渐缩小, 到了八、九年级, 学生在四个分析层次的得分比例呈现均衡分布, 学生数学符号意识在GS、LY、LT、CB四个分析层次的得分比例随着年级的升高逐渐表现出均衡分布。
图3 四个分析层次在测试卷结构中的得分比例
(二) 不同年级学生在数学符号意识上的差异
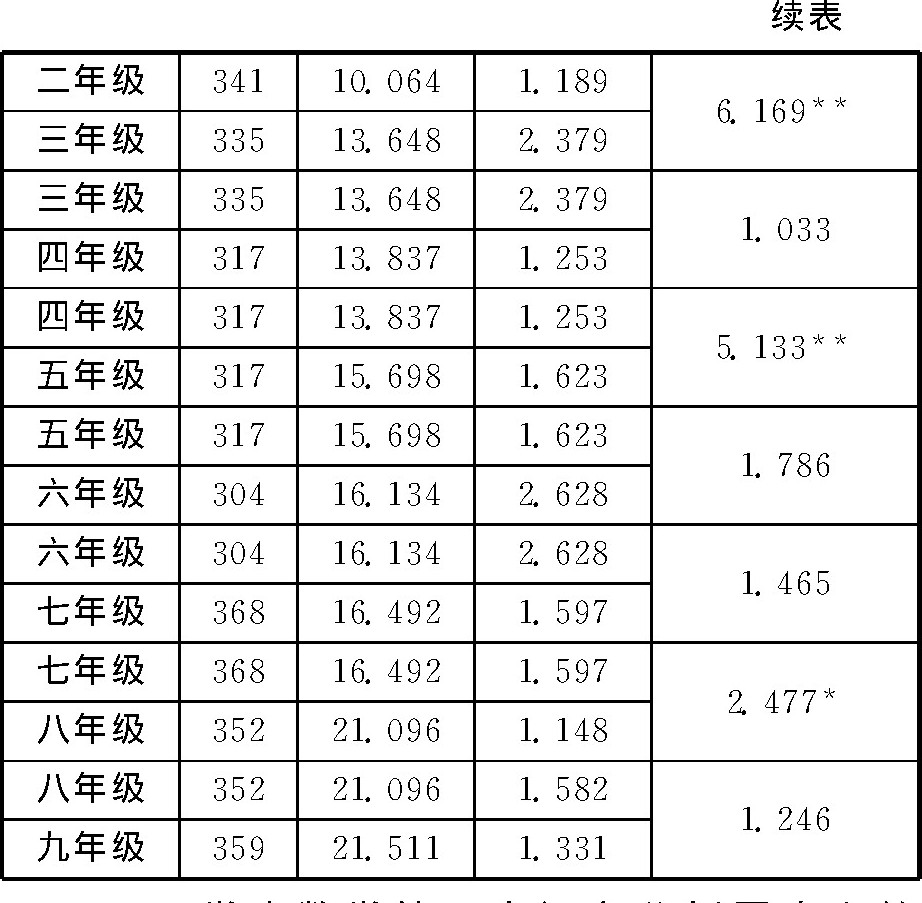
为了了解不同年级学生在数学符号意识上的差异, 我们分别对相邻年级学生的数学符号意识做了t检验, 结果如表6所示。由表6可以看出, 二年级与三年级学生在数学符号意识上存在显着差异, 四年级与五年级学生在数学符号意识上存在显着差异, 七年级与八年级学生在数学符号意识上存在显着差异, 其他两个相邻年级之间的学生在数学符号意识上均没有显着差异。
表6 不同年级学生在数学符号意识上的差异

表6 不同年级学生在数学符号意识上的差异
(三) 学生数学符号意识在分析层次上的节点
为了寻找不同年级学生在数学符号意识各分析层次上的节点, 我们分别对相邻年级学生数学符号意识各分析层次做了t检验, 结果如表7所示。
表7 节点年级学生在数学符号意识各分析层次的差异
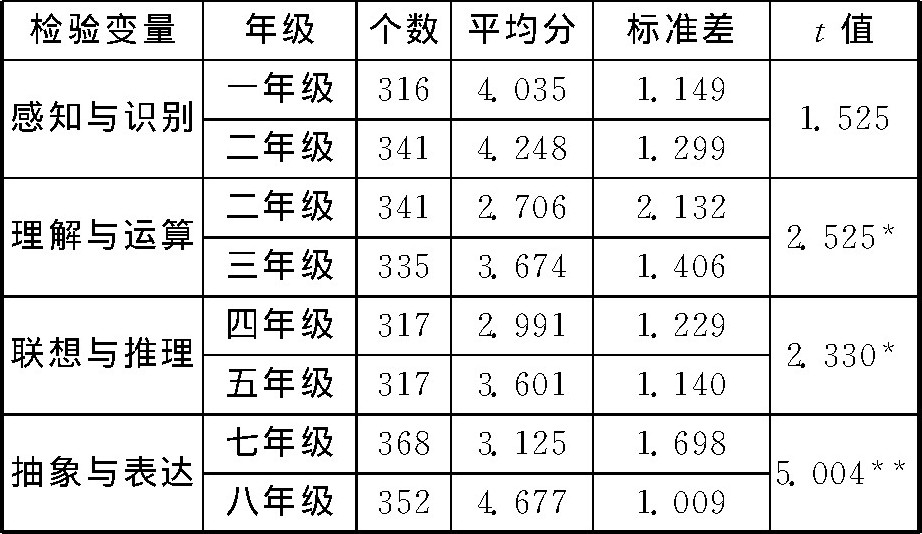
由表7可以看出, 一年级与二年级在数学符号意识感知与识别层次不存在显着差异, 并且两个年级平均分均高于3.6分 (各层次测试卷总分的60%) ;二年级与三年级学生在数学符号意识理解与运算层次存在显着差异, 三年级在该层次的平均分高于3.6分;四年级与五年级学生在数学符号意识联想与推理层次存在显着差异, 五年级在该层次的平均分高于3.6分;七年级与八年级学生在数学符号意识抽象与表达层次存在显着差异, 八年级在该层次的平均分高于3.6分。
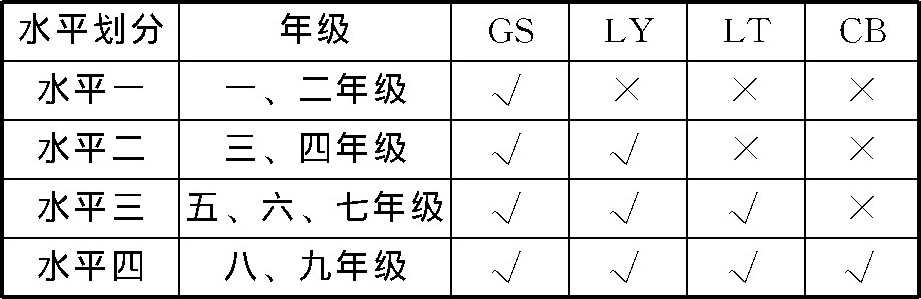
义务教育阶段学生数学符号意识发展水平的划分出现三个节点, 即二年级与三年级、四年级与五年级、七年级与八年级, 三个节点在六个年级各分析层次上的表现如表8所示。二年级学生只能达到数学符号意识感知与识别层次, 并未达到数学符号意识理解与运算层次;三年级学生已经达到数学符号意识的感知与识别、理解与运算两个分析层次, 但并未达到数学符号意识的联想与推理、抽象与表达两个分析层次;四年级学生只能达到数学符号意识的感知与识别、理解与运算两个分析层次, 并未达到数学符号意识的联想与推理层次;五年级学生已经达到数学符号意识的感知与识别、理解与运算、联想与推理三个分析层次, 但并未达到数学符号意识的抽象与表达层次;七年级学生只能达到数学符号意识的感知与识别、理解与运算、联想与推理三个分析层次, 并未达到数学符号意识抽象与表达分析层次;八年级学生已经达到数学符号意识的抽象与表达分析层次。
表8 学生数学符号意识节点的划分
四、结论与讨论
(一) 学生数学符号意识发展水平随年级的增长不断升高
义务教育阶段学生数学符号意识的发展水平是从简单到复杂, 从低级到高级, 从具象到抽象, 呈现层次性发展的。学生数学符号意识的发展与形成要经历漫长的过程, 随着学生年级的增长其数学符号意识的发展水平逐渐升高。任何年级学生的数学符号意识都同时具有具体的成分和抽象的成分, 它们之间的主次关系与相互联系随着年级的高低以及智力活动的性质而发生变化。低年级学生的数学符号意识在很大程度上与具体事物联系着, 要求他们指出最主要的、本质的东西, 常常是比较困难的。
(二) 学生数学符号意识发展水平与学段的划分不一致
《标准 (2011年版) 》中指出, 一年级至三年级为第一学段, 四年级至六年级为第二学段, 七年级至九年级为第三学段。这与义务教育阶段学生数学符号意识发展阶段是不一致的。从这个意义上来看, 虽然小学与初中的数学教学是分开的, 课程标准是分段的, 但是在学生数学符号意识的发展上具有一定的连贯性。这里给我们的启示是, 在培养学生数学符号意识的时候要循序渐进, 认真分析小学与初中的关系与衔接, 注重标准中的学段与有关数学符号教学之间的联系, 在教学设计中, 既要关注小学、初中的分段, 也要重视符号意识发展的规律。在中小学数学符号意识的衔接上, 六、七年级整体地、系统地进行思考与设计是非常重要的。根据不同水平学生的表现, 我们可以看出, 将数学始终如一地全盘符号化、过度符号化的教学, 也是不对的, 需要一个半符号化系统的过渡, 以文字语言为基础进行适当符号化。
(三) 义务教育阶段学生数学符号意识可以划分为四个发展水平
一年级和二年级的特征是数学符号意识具有可感性与具体化, 我们称之为经验观察水平, 具体表现为:学生可以通过整体来辨认数学符号, 并区分不同类型的数学符号 (如字母、图形、关系式等) ;学生能够借助具体事物, 用标准的或者不标准的名称对数学符号进行直观性描述;学生知道数学符号的独特性, 但无法解释数学符号的本质内涵, 无法利用数学符号的特征对数学符号进行概括的论述, 如学生知道字母和数字是不同的, 但是不能理解字母可以表示一类数量。
三年级和四年级的特征是数学符号意识具有深刻性与特殊化, 我们称之为本质内化水平, 具体表现为:学生能够理解数学符号的意义, 并以此分析数学符号所代表的本质与非本质内涵;学生能够解释同一个数学符号在不同数学情境下的意义, 但无法建立不同数学符号之间的关联;学生能够脱离具体事物, 模仿数字将数学符号作为运算对象, 并对其进行运算, 但无法解释所得结果的一般性, 如学生在符号运算的时候, 不再关注“□”是苹果还是橘子, 是5还是6。
五年级、六年级和七年级的特征是数学符号意识具有逻辑性与形式化, 我们称之为理性辩证水平, 具体表现为:学生能够建立不同数学符号之间的相互关联, 形成数学符号的网络结构, 可以利用特例尝试的方法提出猜想, 并在特例的基础之上, 利用数学符号得出一般规律和结论;学生能够利用数学符号进行演绎推理论证和猜想, 能够比较同一个定理不同的符号论证方法;学生能够利用数学符号解释论证所得结果的一般性。
八年级和九年级的特征是数学符号意识具有整体性与模式化, 我们称之为结构普适水平, 具体表现为:学生能够利用数学符号建立模型或者法则, 并在一般意义上表达具体的数量关系;学生能够实现不同数学符号表达之间 (如字母、图形、表达式等) 的相互转化, 并比较不同符号表达之间的优点与缺点;学生能够利用数学符号进行符号思考, 在解决问题的过程中, 实现数学符号作为现实世界与数学世界之间联结的价值。
本研究中关于数学符号意识发展水平的划分与国内外数学教育心理研究的成果存在一致的地方。
从数学核心素养的视角来看, 数学符号意识应该与其他数学核心素养 (数感、空间观念、数据分析观念等) 具有共性的一面, 在本研究中, 整个义务教育阶段学生数学符号意识的发展水平是进阶的, 随着年级的增长不断升高, 这与其他数学核心素养的相关研究成果是一致的。
从思维发展的视角来看, 学生抽象逻辑思维要经历初步逻辑思维、经验逻辑思维和包括辩证思维在内的理论型思维三个阶段。从总体上来看, 到小学高年级, 学生不仅能够进行具体形象思维, 还能进行抽象逻辑思维, 辩证思维也开始萌芽, 思维结构也开始从不完善向比较完善过渡。[20]有研究指出, 小学四年级是思维发展的关键时期, 初中阶段的思维发展出现质的飞跃是在八年级, 处于思维发展的转折点。[21]在本研究中, 四年级与八年级也同样是数学符号意识发展水平的关键节点, 表现为学生的数学符号意识开始从经验型思维向理论型思维转化, 这与一些学者的研究结论具有一致性。
从学生认知的视角来看, 义务教育阶段主要处于皮亚杰划分的认知发展阶段的后面两个阶段, 即具体运算阶段 (七八岁至十一二岁) 和形式运算阶段 (十一二岁开始) 。[22]儿童在12岁时 (五年级或者六年级) 进入形式运算阶段, 到了这个阶段, 事物的表述形式是符号, 人类思维能够用符号形式来处理具体的事物, 儿童能够脱离以往经验的束缚, 实现逻辑的数学推理, 不再拘泥于具体运算的经验。
本研究除了以上与其他研究相一致的方面之外, 还具有数学符号意识的特性。本研究立足于整个义务教育阶段, 学生数学符号意识可以划分为四个发展水平, 而其他数学核心素养表现出不同的水平划分。例如, 郭民将小学生数感发展分为三个阶段:数觉阶段、符号阶段、模型 (问题解决) 阶段。[23]刘晓玫将小学生的空间观念划分为三个水平: (完全) 直观想象阶段、直观想象与简单分析抽象阶段、直观想象与复杂分析阶段。[24]
学生数学符号意识的培养需要抓住发展水平的关键节点, 帮助学生强化数学符号意识, 逐步达到不同层次水平。只有经历完整的、充分的数学符号意识的培养过程, 学生才能在数学符号意识水平一的基础上, 逐步过渡到水平二、三、四, 最终建立起一定的数学符号意识。本研究从课程的角度出发, 利用自行编制的学生数学符号意识发展水平测试卷, 对义务教育阶段学生数学符号意识的发展水平及其特征进行了分析和研究, 获得了相关的结论。这些结论对于认识和了解义务教育阶段学生在数学符号意识方面的发展规律和特点提供了重要的事实依据, 希望依据这些结论, 可以根据不同年级学生所处的不同水平, 制定相关的教学策略, 并为今后数学符号意识的培养与评价奠定理论与实证研究的基础。
参考文献:
[1]史宁中.数学思想概论——图形与图形关系的抽象[M].长春:东北师范大学出版社, 2009:38.
[2]曹艳荣.数学教学要重视培养学生的符号感[J].教学月刊 (小学版) , 2004 (11) :19.
[3]王兄.数学教学中的符号感:表象图示意义下的理解[J].中国教育学刊, 2007 (1) :63-65.
[4]J Fey.Quantity[M]//L A Steen.On the shoulders of giants:new approaches to numeracy.Washington D.C:National Academy Press, 1990.
[5]Picciotto H, Wah A.A new algebra:Tools, themes, concepts[J].Journal of mathematical behaviour, 1993 (12) :19-42.
[6]李艳琴, 宋乃庆.小学低段数学符号意识的含义及其表现形式[J].课程·教材·教法, 2016 (3) :92-97.
[7]王成营.浅谈数学符号意义获得能力及其在问题解决中的培养[J].课程·教材·教法, 2012 (11) :74-78.
[8]周东明, 姚相全.何谓小学生的符号感?[J].人民教育, 2010 (19) :47-48.
[9]孔凡哲, 曾峥.数学学习心理学[M].北京:北京大学出版社, 2009:23.
[10]李艳琴, 宋乃庆.小学低段数学符号意识测评指标体系的初步构建[J].教育学报, 2016 (4) :23-28, 38.
[11]张号, 童莉, 黄翔.数学符号从“感”到“意识”[J].数学教育学报, 2014 (1) :100-102.
[12]史炳星, 马云鹏, 唐复苏.在解决问题的过程中发展学生的符号感[J].数学教育学报, 2002 (2) :57-60.
[13]杨红萍, 喻平.数学语言对数学阅读的影响研究[J].数学通报, 2010 (9) :19-23.
[14]王林全.发展学生数学符号意识的要领[J].数学通报, 1996 (5) :4-8.
[15]Arcavi A.Symbol sense:Informal sense-making in formal mathematics[J].For the learning of mathematics, 1994, 14 (3) :24-35.
[16]中华人民共和国教育部.义务教育数学课程标准 (2011年版) [S].北京:北京师范大学出版社, 2012:6.、
[17]Pierce R, Stacey K.A framework for algebraic insight[C]//J Bobis, B Perry, M Mitchelmore.Proceedings of the 24th annual conference of the mathematics education research group of Australasia, Numeracy and Beyond Sydney:MERCA.2001:418-425.
[18]鲍建生, 周超.数学学习的心理基础与过程[M].上海:上海教育出版社, 2009:323-325.
[19]雷新勇.大规模教育考试:命题与评价[M].上海:华东师范大学出版社, 2006:100-134.
[20]李艳红.教育心理学[M].北京:中国社会科学出版社, 2012:29-30.
[21]郑君文, 张恩华.数学学习论[M].南宁:广西教育出版社, 1996:90.
[22]左任侠, 李其维.皮亚杰发生认识论文选[M].上海:华东师范大学出版社, 1991:21.
[23]郭民.小学生数感的发展与特征研究[D].长春:东北师范大学, 2009.
[24]刘晓玫.小学生空间观念的发展规律及特点研究[D].长春:东北师范大学, 2007.
注释:
1 各学段测试卷的总分为24分。