人脑模板的构建方法和现状综述

　　摘    要：　脑模板是能代表一个群体的大脑模型, 包含大脑结构及分区标签等信息, 在脑神经影像学分析领域具有重要作用。脑模板可为群体分析提供标准归一化空间, 将先验知识如分割图谱和解剖标识映射到新图像上进行分析。构建脑模板包括图像预处理、图像配准和模板构建三步。随着脑影像学处理和分析技术的提高, 脑模板的质量逐渐提升、应用范围逐渐扩大。本文对人脑模板的构建方法和应用进展进行综述。

　　关键词：　脑模板; 磁共振成像;

　　Abstract：　Brain atlas, as a representative brain model of a population, usually includes brain structure image, brain

　　人脑结构和功能非常复杂, 且由于性别、年龄、地域以及生理状态等差异, 不同人群大脑形状和大小均有所不同。此外, 成像技术和计算方法的差异也会影响对图像的综合分析[1], 故空间标准化是研究大脑的重要步骤。脑模板包含大脑神经解剖学位点的结构和功能信息, 可为空间标准化提供基准。参照脑模板可对特定大脑图像进行分析, 现已广泛用于神经影像学领域, 如诊断疾病、定位病灶及制定手术方案等[2]。脑模板的设计对分析神经影像数据至关重要, 尤其是人群特异性脑模板, 有助于精准分析数据。本文对人脑模板的构建方法和现状进行综述。

　　1 脑模板构建方法

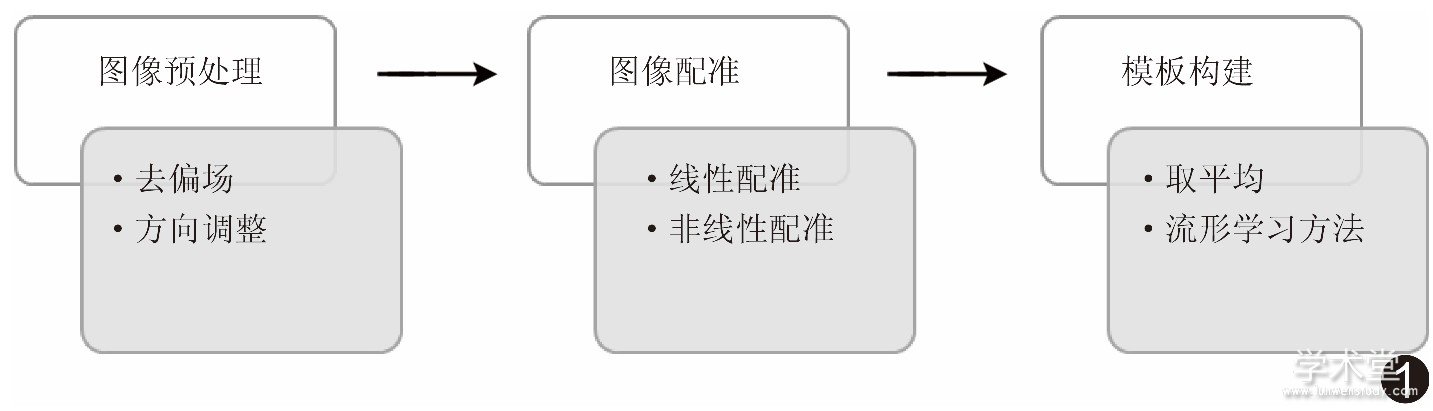
　　脑模板的构建包括图像预处理、图像配准和模板构建 (图1) 。

　　1.1 图像预处理

　　构建脑模板需高质量MR图像, 数据存储格式为DICOM、ANALYZE或NIFTI。构建脑模板前, MR图像需经一系列预处理步骤[3]以提高脑模板质量, 包括去偏场及方向调整等[4]。

　　1.2 图像配准

　　构建脑模板时需将图像配准为标准图像, 使所有图像标准化到同一空间。标准图像的选取方法包括: (1) 随机选取; (2) 从标准人脑模板数据库中选取; (3) 与标准人脑模板进行线性配准, 选取匹配效果最佳的图像[5]。之后将所有图像与选取的标准模板进行配准。有学者[5,6]采用线性变换进行配准构建MNI152和MNI305人脑模板;还有学者[6]将452幅人脑图像通过仿射变换获得ICBM452人脑模板Air-12版本。由于线性配准仅将图像大致对齐, 故通过线性变换构建的脑模板的脑结构细节较为模糊。

　　为获得包含更多细节、显示解剖结构更为清晰的脑模板, 多项研究[7,8,9]提出非线性配准方法。与ICBM-452人脑模板Air-12版本相比, warp-5版本的脑模板利用AIR软件先进行线性仿射变换, 再行5阶多项式非线性变换, 配准方法更为精确, 可提供更多皮层的细节信息[9]。此外, 还有更为先进的非线性配准方法用于脑模板创建, 具体如下。

　　1.2.1 微分同胚方法

　　为解决模板选取时的引入偏差, Xie等[7]提出基于微分同胚的方法建立无偏模板, 并以2岁儿童的MRI数据构建了无偏模板和概率图谱。Joshi等[8]也采用微分同胚映射方法构建了皮质脑沟模板。Schuh等[9]采用微分同胚配准构建4D脑模板和生长模型, 发现可用相反一致性变换的Log-Euclidean方法更好地反映平均形态。构建微分同胚转换的一种方法是解决如下非稳态转运方程:

　　其中u (Φ (y, t) , t) ∈H是希尔伯特空间H上时间无关且平滑的速度向量场。对于最初的映射, 相当于在t=0时确认转换Φ (y, 0) ;对于最后的映射, 速度场u的终点可通过计算单位时间间隔t∈[0, 1]的集合获得:

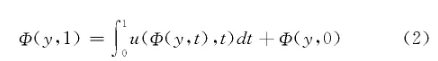
　　根据偏微分方程的解的存在性和独特性定理, 式 (1) 的解由速度场u (Φ (y, t) , t) 和初始条件Φ (y, 0) 确定。微分同胚路径Φ不仅可微, 还可保证集合的一一映射, 对于分析不同解剖结构在形态和功能上的关系具有重要意义。此外, 微分同胚框架可定量测量不同结构或形状之间的距离[10]。

　　图1 脑模板构建流程图

　　1.2.2 图像集配准

　　图像集配准可根据群体数据构建无偏模板。与成对配准相比, 图像集配准可同时为所有图像估计转换场, 而无须以特定图像作为模板。

　　在无偏图像集配准框架中, 通过迭代将N个图像配准到组平均图像获得形变场;在第t轮配准时, 通过对当前形变后图像的灰度取平均获得组平均图像Mt:

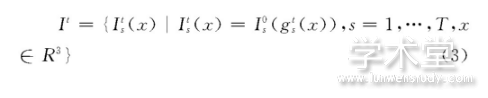
　　当前变换场是:

　　每个gst的计算都是将Mt-1作为模板, 将Is0作为待配准图像, 其中G0是最初的仿射变换。

　　组平均图像的估计看作统计估计问题:

　　其中dist (e, gst) 是灰度变化e和gst之间的距离。

　　图像集配准方法是先用迭代方法计算组的均值图像, 再将其他图像与均值图像进行配准[11]。但均值图像一般较为模糊, 细节缺失, 而图像集配准过程中保持组均值图像的清晰度具有重要意义。Wu等[11,12]提出SharpMean方法, 即在配准时采用自适应权重策略, 并发现其配准精确度高于传统方法;同时, 应用基于树的配准来提高每个对象的配准精确度, 在每次配准时均以最小生成树来保证配准结果的鲁棒性。为解决图像之间的形变问题, Lombaert等[13]提出一种新的图像谱集Log-Demons框架, 通过扩展对称Log-Demons算法, 可同时进行模板构建与图像集配准。

　　1.3 模板构建

　　将配准后的图像均值化, 可获得MNI152、MNI305和ICBM452脑模板。取平均时可直接取平均或加权取平均, 将所有图像均用来构建模板可增加模板的细节信息, 但也会引入噪声, 使图像中有关结构模糊不清。Shi等[14]提出基于字典学习的方法, 用少量图像块来稀疏表示模板中的每一个图像块。采用基于块的稀疏表示方法, 可在模板上展现较多解剖细节;同时, 对组结构的约束和重叠块的使用可确保相邻块之间的解剖连续性。有学者[14]采用基于块的稀疏表示方法对73名新生儿的MR图像构建无偏的脑模板, 发现脑模板的质量增强, 且可发现更多的解剖细节, 有助于将新生儿数据标准化。

　　由于图像集配准算法不能保证全局最优解, 故无偏微分同胚算法构建的模板较模糊。考虑到图像清晰度以及旋转不变性, Xie等[7]引入商空间的流形学习, 用不变矩阵扩展流形学习方法, 通过流形结构将图像分成更均匀的子集, 每个子集都能用一个模板图像表示;同时还以两步算法建立脑模板:用无监督或半监督方法将输入图像分成亚组, 在每个亚组用公式表示一个凸优化问题来定位模板;其结果表明, 此法不仅可发现不同年龄组的脑结构变化, 还可保留重要的结构细节。

　　有研究[15]首先将图像配准到标准空间 (个体内线性配准) , 以ANTS软件的SyN算法实施图像配准、核回归框架构建模板, 再用非刚性配准方法将12个模板配准到标准空间获得中国人标准脑模板Chinese2020, 包含20~75岁、以5年为间隔构建的12个脑模板 (图2) 。

　　图2 中国人标准脑模板[15]

　　A.冠状位;B.矢状位;C.轴位

　　2 4D脑模板构建

　　儿童大脑的体积、形状和外观随年龄增长而变化。为描述大脑在发育时期的动态变化, 通常会构建随时间变化的脑模板。关于构建新生儿脑模板的研究较多见。Serag等[16]提出用自适应核回归法建立新生儿大脑4D模板。Serag等[17]用自适应核回归法对204例早产儿在孕28~44周时大脑T1WI和T2WI进行建模, 生成与年龄相关的解剖模板 (图3) 。Alexander等[18]采用分割方法构建新生儿脑模板图, 将成年人的脑皮层模板复制到新生儿脑模板上, 从10个新生儿T2WI手动分割出基底核、丘脑、小脑和其他皮质层下区域, 生成100个脑区域, 最后构建出包含皮质和皮质层下区域详细轮廓的脑模板。Shi等[19]对95名正常婴儿在3个年龄阶段 (出生、1岁和2岁) 的MRI数据均成功构建脑模板、组织概率图和脑分割图, 获取年龄特异性模板的纵向对应关系。胎儿的脑成像难度较大以及胚胎期大脑的快速变化均使胎儿脑模板构建受限。Gholipour等[20]将81胎孕19~39周正常胎儿的MRI数据, 结合空间的对称微分同胚形变配准和时间上的核回归法成功构建无偏4D胎儿脑模板。Schuh等[9]采用微分同胚的Log-Euclidean方法构建4D脑模板, 以对象间的成对变换构建模板的时间序列, 导出均值生长的纵向形变模型。Sanchez等[21]收集494名4.5~19.5岁儿童的823次MR扫描图像, 以6个月为年龄间隔, 构建头部、脑部和分割模板, 获得儿童年龄特异性MRI模板。

　　图3 早产儿在孕28~44周的脑模板[17]

　　A.T1WI;B.T2WI

　　3 小结与展望

　　不同种族、不同年龄以及不同模态的脑模板对于探索不同群体之间脑结构和脑功能异同、观察大脑随年龄增长的变化趋势、术中定位及定量分析大脑等具有重要作用。随着大数据共享的发展, 可获得的脑神经影像学的数据越来越多, 基于大数据创建更具代表性的脑模板已成为趋势。根据特殊群体创建的人群特异性脑模板也有助于分析特定群体的大脑结构。随着脑影像学技术的发展, 将逐渐出现更多模态的脑模板, 为探索更细微的脑结构和脑功能提供参考。

　　参考文献:

　　[1] Wu BW, Barr S.Applications of whole brain tractography and implications for clinical practice.Cureus, 2017, 9 (10) :e1753.
　　[2]Mega MS, Dinov ID, Mazziotta JC, et al.Automated brain tissue assessment in the elderly and demented population:Construction and validation of a sub-volume probabilistic brain atlas.Neuroimage, 2005, 26 (4) :1009-1018.
　　[3]Dinov ID, Valentino D, Shin BC, et al.LONI visualization environment.J Digit Imaging, 2006, 19 (2) :148-158.
　　[4]Zhuang AH, Valentino DJ, Toga AW.Skull-stripping magnetic resonance brain images using a model-based level set.Neuroimage, 2006, 32 (1) :79-92.
　　[5]Mandal PK, Mahajan R, Dinov ID.Structural brain atlases:Design, rationale, and applications in normal and pathological cohorts.J Alzheimer Dis, 2012, 31 (Suppl 3) :S169-S188.
　　[6]Lalys F, Haegelen C, Ferre JC, et al.Construction and assessment of a 3-T MRI brain template.Neuroimage, 2010, 49 (1) :345-354.
　　[7] Xie Y, Ho J, Vemuri BC.Multiple atlas construction from a heterogeneous brain MR image collection.IEEE Trans Med Imaging, 2013, 32 (3) :628-635.
　　[8] Joshi SH, Cabeen RP, Sun B, et al.Cortical sulcal atlas construction using a diffeomorphic mapping approach.Med Image Comput Comput Assist Interv, 2010, 13 (Pt 1) :357-366.
　　[9] Schuh A, Murgasova M, Makropoulos A, et al.Construction of a 4D brain atlas and growth model using diffeomorphic registration//Springer.International Workshop on Spatiotemporal Image Analysis for Longitudinal and Time-Series Image Data.Heidelberg:Springer, 2014:27-37.
　　[10] Blaiotta C, Freund P, Cardoso MJ, et al.Generative diffeomorphic atlas construction from brain and spinal cord MRIdata.[2018-10-20].http://discovery.ucl.ac.uk/id/eprint/1563919
　　[11]Wu G, Jia H, Wang Q, et al.SharpMean:Groupwise registration guided by sharp mean image and tree-based registration.Neuroimage, 2011, 56 (4) :1968-1981.
　　[12]聂彬彬, 赵书俊, 单保慈.动物标准脑模板建立的研究进展.中国医学影像技术, 2009, 25 (6) :1103-1105.
　　[13] Lombaert H, Grady L, Pennec X, et al.Groupwise spectral Log-Demons framework for atlas construction//Springer.International MICCAI Workshop on Medical Computer Vision.Heidelberg:Springer, 2012:11-19.
　　[14] Shi F, Wang L, Wu G, et al.Atlas construction via dictionary learning and group sparsity//Springer.International Conference on Medical Image Computing and Computer-Assisted Intervention.Heidelberg:Springer, 2012:247-255.
　　[15] Liang P, Shi L, Chen N, et al.Construction of brain atlases based on a multi-center MRI dataset of 2020Chinese adults.Sci Rep, 2015, 5:18216.
　　[16] Serag A, Kyriakopoulou V, Rutherford MA, et al.A multichannel 4D probabilistic atlas of the developing brain:Application to fetuses and neonates.Annals, 2012, 2012 (3) :1-14.
　　[17]Serag A, Aljabar P, Ball G, et al.Construction of a consistent high-definition spatio-temporal atlas of the developing brain using adaptive kernel regression.Neuroimage, 2012, 59 (3) :2255-2265.
　　[18] Alexander B, Murray AL, Loh WY, et al.A new neonatal cortical and subcortical brain atlas:The melbourne children's regional infant brain (M-CRIB) atlas.Neuroimage, 2017, 147:841-851.
　　[19] Shi F, Yap PT, Wu G, et al.Infant brain atlases from neonates to 1-and 2-year-olds.PLoS One, 2011, 6 (4) :e18746.
　　[20] Gholipour A, Rollins CK, Velasco-Annis C, et al.A normative spatiotemporal MRI atlas of the fetal brain for automatic segmentation and analysis of early brain growth.Sci Rep, 2017, 7 (1) :476.
　　[21]Sanchez CE, Richards JE, Almli CR.Age-specific MRItemplates for pediatric neuroimaging.Dev Neuropsychol, 2012, 37 (5) :379-399.