摘 要: 利用有限元软件COMSOL模拟了声波打在不同属性粒子上的散射现象,并且研究了粒子对声波的吸收,其中考虑了粘滞损失、热传导损失和散射。结论是不同属性粒子对声波的散射效果不同,而且不同属性粒子对声波的吸收也不同,其中阻抗越大,粒子对声波的吸收越小。
关键词: COMSOL软件; 粒子属性; 声波散射; 声波吸收;
Abstract: The scattering phenomenon that sound waves hitting particles of the different properties is simulated by the finite element software COMSOL,and the particle absorbing sound waves is researched,which consider the viscous loss,heat loss and scattering. The conclusion is that the scattering effect of different attributes on acoustic is different,and different properties of particles absorbing sound waves are different,the greater the impedance of the particles is,the smaller the particle absorbing sound waves is.
Keyword: COMSOL software; particle properties; acoustic scattering; acoustic absorption;
0、 引言
在超声波多相流检测中[1,2],对于声波打到粒子上,粒子对声波的作用,通过实验不容易获得且代价昂贵,但是利用仿真实现比较容易。本文对声波打在粒子的现象利用COMSOL软件进行了建模,通过仿真获得了不同粒子对声波的散射和对声波的吸收影响。

1 、建模
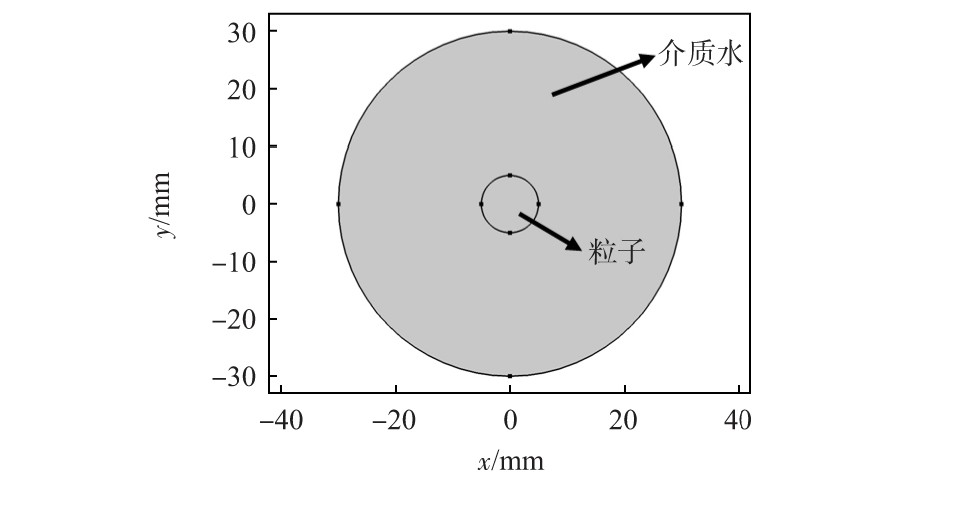
模型空间维度选择2D,接口选用声固耦合接口,研究类型为频域,几何图形如图1所示,内圆代表粒子,半径为5 mm,外圆代表介质,半径为30 mm,介质材料为水,水中的声速c=1 473 m/s,密度ρ=997 kg/m3,内圆材料设为自定义材料,声场作用域选择介质水,固体力学作用域选择粒子。声波从左侧以平面波入射,初始声压值为1 Pa,频率f为60 k Hz,外圆边界设为辐射边界,使声波能完美辐射,相当于外圆介质无限大。内圆的边界设为声固耦合边界,在边界上将产生声学和固体力学的耦合作用,网格采用自由三角形剖分,其最大尺寸设为c/6f,求解过程分为2个研究,第一个研究只研究声场,此研究中把粒子看作刚性不动粒子;第二个研究选择声场和固体力学,将研究两种物理场在介质和粒子上的相互作用。
图1 几何图形
2 、粒子上的散射
不同频率的声波入射到粒子上的散射现象已经被众人所熟知,波长与粒子粒径的比值对散射起着主要作用,当波长远大于粒径,声波散射服从瑞利散射[3]。另外在粒子对声波的散射研究过程中,考虑的大多是刚性不动粒子,而对于非刚性粒子的散射研究的并不多[4]。因此在仿真中,研究刚性粒子和非刚性粒子对声波散射的不同有一定意义。本文首先考虑刚性不动粒子对声波的散射现象,然后考虑自定义材料粒子对声波的散射作用,在散射中自定义材料设为软件自带材料库中的铝3003—H18。通过仿真能获得散射的声压分布、声压级分布、远场压力等,刚性粒子和铝材料粒子的远场声压如图2所示。
图2 刚性粒子和铝材料粒子的远场声压
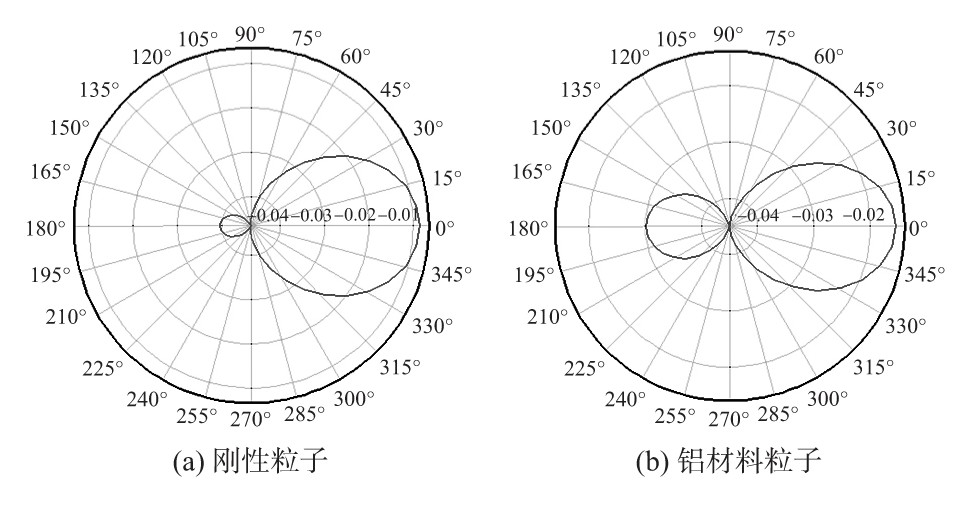
由以上两个对比图可以看出:粒子属性的不同将影响声波的散射。为了进一步查看粒子属性对声波散射的影响。在后处理中选取一条二维截线,截线的两个端点为(-30,0)和(30,0)。选取截线上的声压值进行绘图,结果如图3所示。
图3 刚性粒子和铝材料粒子的绝对声压
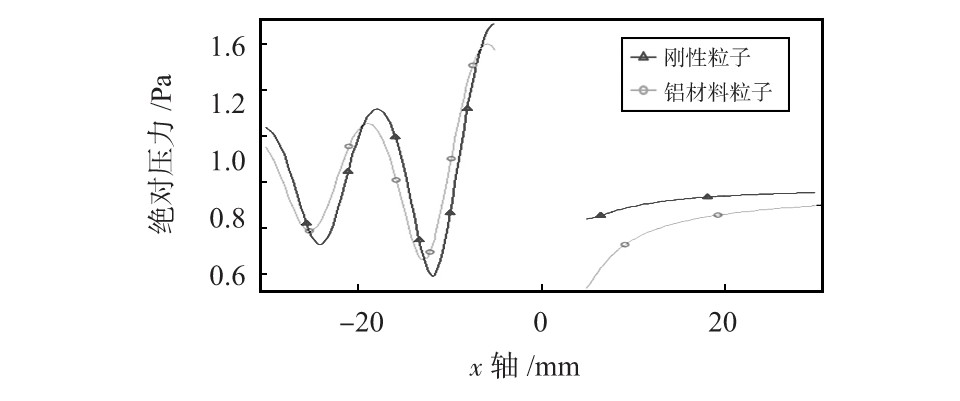
从图中可以看出铝材料粒子环境下,粒子前向区域声压值在不同的位置声压值不同,在高峰位置略小于刚性粒子声压值,在低峰位置略高于刚性粒子的声压值(前向区域指x轴的负区域)。而在后向区域,铝材料粒子的声压值总小于刚性粒子的声压值。因此可以知道,当粒子的属性不同时声波的散射也不同。
3 、粒子上的声吸收
声吸收的主要因素包括热损失、黏性损失、吸收损失和散射[5]。当一个平面压缩波通过连续介质入射到一个粒子上,粒子将反射一个压缩波,在粒子内也产生一个压缩波。同时在球的内部和外部也会产生热波和剪切波。粘性损失主要是由于粒子和连续介质的密度差引起的,这种密度差导致粒子和介质的相对滑动。热损失是由于粒子表面附近的温度梯度产生的。吸收损失与材料有关,是介质本身的吸收。声散射与光散射类似,粒子仅改变了入射波的传播方向,使这部分声波不能到达接收换能器,而不改变声波的性质[6,7]。在声吸收的仿真研究中,声场的设置是在上面散射研究的基础上添加粘滞和热传导损耗,粘滞和热传导的添加是在“压力声学,频域接口>压力声学>压力声学模型>流体模型”中选择“热传导和粘性”,当选择完成后,在“材料”中会自动添加相关参数,如体粘滞系数、动力粘度、比热率、常压热容等,因为文中模型中的材料来自软件中的材料库,其中这些参数已经定义,不需要手工添加。而在固体力学的设置中,在“固体力学接口>线性材料>指定”里选择剪切模量,因为材料库中铝3003—H18的剪切模量未给出,所以需要自己添加,此模型定义为80 GPa。当粒子是刚性粒子或自定义的材料粒子时(仍以铝3003—H18作为自定义材料的初始材料),分别计算外圆上声强的积分,声强为
式中p为总声压,ρc为声阻抗。改变自定义材料的粒子密度后,总声强I_t和散射声强I_s在整个外圆线上的积分值如表1所示,可以看出密度越大总声强和散射声强越大,即粒子上吸收的声能越小。
表1 粒子密度不同对声强的影响

固体中杨氏模量和材料密度之比等于速度的平方,通过改变粒子杨氏模量可以改变粒子中的声速。表2是改变粒子杨氏模量时总声强和散射声强在整个外圆上的线积分值。可以看出杨氏模量越大总声强和散射声强越大,即声速越大粒子吸收的声能越少。
表2 粒子杨氏模量不同对声强的影响

材料密度和材料中声速的乘积是材料的声阻抗[8]。从上面两个表中能够看出粒子密度越大或声速值越大粒子对声波的吸收越小,所以能够推得,粒子的声阻抗越大,粒子对声波的吸收作用越小。
4、 结论
从仿真中,可以看出铝粒子的散射场与刚性粒子散射场不同,当把接收换能器放在坐标(30,0)时,接收到的声压小于刚性粒子条件下的声压。当改变粒子的密度和声速时,可以看出密度越大或声速越大,声强在整个外圆上的积分越大,也就是说粒子吸收的能量越小。因此能够看出,粒子的阻抗越大,粒子对声波的吸收越小。
参考文献
[1] CARVER L. Using multiphysics simulation to prevent building damage[J]. COMSOL News,2014,38(7):22-23.
[2]徐轶,徐青.基于COMSOL Multiphysics的渗流有限元分析[J].武汉大学学报(工学版),2014,47(2):165-170.
[3]许肖梅.声学基础[M].北京:科学出版社,2003:204-217.
[4]李树榜,李书光,刘学锋.固体中圆柱形孔脉冲超声波散射的有限元模拟[J].声学技术,2007,26(3):417-421.
[5]苏明旭,沈建琪,徐峰,等.一种颗粒系超声衰减谱的改进计算方法[J].声学技术,2010,29(6):592-594.
[6]蔡小舒,苏明旭,沈建琪,等.颗粒粒度测量技术及应用[M].北京:化学工业出版社,2010:180-181.
[7]刘会彬,郑阳,郑晖.超声波散射有限元模型中单一模态入射研究[J].声学技术,2016,35(2):130-136.
[8] 乔榛.超声法一次风流速和煤粉浓度在线测量研究[D].南京:南京理工大学,2012.