物流配送中心选址中改进版灰狼优化算法的应用

　　摘    要：　针对物流配送中心选址模型具有多约束和非线性的特点，导致难以求解的问题。提出一种改进灰狼优化算法的求解策略。文章通过引入交叉变异策略，改进了传统灰狼算法在迭代后期易早熟收敛的问题；通过加入双种群寻优策略，丰富了灰狼算法的种群多样性，提高了算法的收敛速度。将改进后的灰狼算法针对物流配送中心选址模型进行求解，实验结果表明，该改进灰狼优化算法具有较高的全局搜索能力，针对物流配送中心选址模型具有较高的搜索精度，很大程度的提高了物流配送效率。

　　关键词 :     灰狼优化算法;物流配送中心选址;交叉变异;双种群寻优;

　　Abstract：　Aiming at the problem that the location model of logistics distribution center has the characteristics of multi constraints and nonlinearity, which is difficult to be solved, an improved gray wolf optimizer(GWO) is proposed. In this paper, by introducing the cross mutation strategy, the issue of premature convergence of the traditional GWO in the later stage of iteration is improved;by adding the dual population optimization strategy, the population diversity of GWO is enriched and the convergence speed of the algorithm is increased. Using the improved GWO to solve the location model of logistics distribution center, the experimental results show that the improved GWO has high global search ability, and high search accuracy for the logistics distribution center location model, which greatly improves the logistics distribution efficiency.

　　Keyword：　gray wolf optimizer; location of logistics distribution center; cross mutation; double population optimization;

　　0、 引言

　　随着网络经济的迅速发展，线上购物在人们生活中的普及程度也越来越高，物流配送产业随之成为了国家的重点产业之一[1]。物流配送的主要内容分为配送中心选址模型优化和物流配送路径优化两个方面，其中配送中心选址模型优化是提高配送效率的核心问题[2]。配送中心位置的合理选取，可以有效地节约配送路径，降低配送时间，节约配送成本。物流配送中心选址模型是一类具有多约束和非线性的复杂数学模型，各约束之间具有耦合性，因此众多学者开始针对此问题进行了深入的研究。

　　文献[3]提出一种基于主动集算法的配送中心选址策略，在主动集算法中加入惩罚函数，增强算法的全局收敛性，优化后求解所得配送中心位置使配送成本最小化。文献[4]提出一种改进模拟退火算法的物流配送中心选址策略，通过加入粒子群算法提高算法的收敛精度，提高了求解配送中心模型的优化速度。文献[5]提出一种改进帝国算法的配送中心选址策略，在优化选址模型的过程中考虑了运输油耗的成本花费和二氧化碳排场污染的两类约束。文献[6]提出一种多目标进化算法的物流配送中心选址策略，该策略在考虑配送成本的同时，对配送时间做出约束，通过动态领域分配策略对算法进行改进，提高了配送中心选址模型优化的求解精度。文献[7]提出一种改进神经网络配送中心选址模型优化策略，节约了配送成本，提高了配送效率。文献[8]提出一种基于K-means聚类方法的物流配送中心选址策略，通过K-means聚类方法对配送中心的聚类单元进行计算，并求解均值，最终得到配送中心的位置。以上策略均从不同方面对优化算法进行改进，提高了算法的收敛精度，但是单一机制的人工智能算法难以有效应用于复杂多约束非线性模型的求解问题上，这是由于单一机制的优化算法在迭代后期会逐渐丧失种群多样性，陷入早熟收敛陷入局部最优。

　　针对上述问题，本文提出一种基于双种群交叉变异灰狼优化算法的物流配送中心选址策略。针对基本灰狼优化算法在迭代后期易早熟收敛的问题，通过引入交叉变异策略，使得灰狼个体在迭代后期可以获得外部扰动力，帮助粒子跳出局部最优，同时将灰狼种群分成两个子种群，提高基本灰狼算法[9]的全局搜索能力。最后将改进灰狼优化算法求解物流配送中心选址模型。

　　1、 物流配送中心选址数学模型

　　对于物流配送中心选址模型而言，设待配送点的个数为N，则需从N个待配送点中，合理的选取M个配送点，作为配送中心，使得配送车辆从M个配送中心出发，到达配送中心对应的配送点距离最短。由于所处地理位置不同，每个配送中心的建设费用以及存放货物的总量不同，因此本文建立了带有多约束条件的物流配送中心选址模型。

　　⑴设每个待配送点所需配送的货物总量不得超过其对应配送中心的货物总量，否则无配送中心可以对其进行配送，该约束的数学模型如下：

　　其中，γi,j表示第j个配送中心所对应的第i个配送点的配送货品的总量。Tj表示第j个配送中心的总货品存放量。

　　⑵设在N个待配送点中，任意一个待配送点的货品均应由距其最近的配送中心进行发货，该约束的数学模型如下：

　　其中，Zi,j为配送中心选取标志，若Zi,j=1，则表示第i个配送点的配送货品应由第j个配送中心进行配送。若Zi,j=0，则表示第i个配送点的配送货品不应由第j个配送中心进行配送。

　　⑶设无配送中心的区域，无配送客户，既无待配送点，该约束的数学模型如下：

　　其中，hj为0或1，当hj为0时，表示第j个配送点不可成为配送中心。当hj为1时，表示第j个配送点可作为配送中心。

　　⑷设在N个待配送点中，任意一个待配送点i到与其对应的第j个配送中心的距离，应小于等于第j个配送中心点可配送的最大距离Lenthmax，该约束的数学模型如下：

　　根据上述约束条件，建立物流配送中心选址模型的数学表达式如下所示：

　　其中，Fj表示第j个配送中心的建设费用。

　　2、 改进的灰狼优化算法

　　2.1、 基本灰狼优化算法

　　基本灰狼优化算法作为一类新型元启发人工智能优化算法，将种群中的全部灰狼个体分四个等级，其中等级最高的作为首领狼，记为α。首领狼负责决策狼群中的各项事务，在算法中表现为决定种群的移动方向。第二等级的狼负责协助首领狼对各项事务就行决策，记为β。第三等级的狼负责整个狼群的狩猎以及防御外敌，记为δ。等级最低的狼负责协助α，β和δ三个等级狼完成任务，可记为ω。因此设灰狼群体的种群规模为NP，维数为ND，对灰狼群体中的全部个体进行位置初始化，其数学表达式如下：

　　其中，i=1,2,?,NP,Xi表示第i个灰狼个体的初始位置。首领狼α负责选定猎物目标，既全局最优解，并与β和δ一起对猎物发起攻击，其数学表达式如下：

　　其中，t=1,2,?,tmax表示算法当前迭代次数，tmax表示算法可执行的最大迭代次数，Xp(t)=(X1p,X2p,?,XDp)表示猎物的当前位置，既当前迭代产生的最优解的位置，因此灰狼优化算法中α，β和δ的位置更新公式为：

　　其中，rand1和rand2为0到1之间的随机数，a为控制因子。此外，由于灰狼个体中的其余个体ω均会围绕α，β和δ的位置进行小范围运动，以待寻找更优的解，因此灰狼优化算法中ω的位置更新公式为：

　　2.2、 灰狼优化算法的改进策略

　　从基本灰狼优化算法的位置更新策略可知，部分灰狼个体会在局部极值点附近进行小范围精确搜索，以期寻找位置更优的全局极值点，此类寻优策略可提高灰狼算法的局部搜索能力。但其缺陷在于算法在迭代后期，种群中的全部个体均在寻优过程中向局部极值点靠近，导致群体在寻优过程中极大程度的丧失群体多样性，导致粒子早熟收敛，陷入局部最优，降低了算法的全局搜索能力。

　　针对上述问题，本文考虑了一种遗传算法与基本灰狼算法相结合的改进算法，目的是帮助陷入局部极值的个体获得一个较大的扰动力，帮助粒子跳出局部最优。在基本灰狼优化算法中加入交叉变异策略，使得灰狼个体在迭代过程中，均会进行不同范围的随机搜索，并且此类搜索过程具有一定的方向指引性可以有效提高算法的全局搜索能力，加快算法在迭代前期的搜索速度。二项式交叉的数学表达式如下：

　　其中，θ1表示交叉因子，rand表示[]之间的随机数。Xti,j表示第i个灰狼个体的第j维分量，Vti,j表示灰狼个体Xti,j进行二项式变异后所得到的位置。二项式变异的数学表达式为：

　　其中，Xts1,j、Xts2,j,Xts3,j分别表示第t次迭代过程中产生的三个位置互异的三个灰狼个体，θ2=0.45为变异因子。

　　加入较差变异策略后，虽然可以有效提高算法的全局搜索能力，但在迭代后期，由于计算量过大，会导致算法计算停滞。针对上述问题，本文考虑一类双种群信息交流寻优策略。该策略将NP个灰狼个体平均分成两个子种群，分别为S1和S2，子种群S1按照基本灰狼优化算法的位置更新策略进行寻优，子种群S2按照加入交叉变异后的灰狼优化算法进行位置更新，并在每次迭代过程中，对两个子种群进行信息交流和贪婪选择，将适应度值较优的个体交换到子种群1中，将适应度值较差的个体交换到子种群2中。

　　具体的改进灰狼优化算法的寻优流程如下。

　　Step1：初始化种群中NP个灰狼个体的初始位置，设置维数ND和最大迭代次数tmax，设置变异因子θ2=0.45，交叉因子θ1=0.35。

　　Step2：将种群平均分为两个子种群S1和S2。SS

　　Step3：计算两个子种群1和2中灰狼个体的适应度，并进行排序，选择出α，β，δ和ω。

　　Step4：对种群S1中的个体按照式⑻、式⑼和式⑽进行位置更新，既按照基本灰狼算法进行寻优。

　　Step5：对种群S2中的个体按照式⑻、式⑼和式⑽进行位置更新后，通过式⑾和式⑿对个体进行交叉变异操作，并对所得解进行边界处理。

　　Step6：计算两个子种群中个体的适应度函数值，并进行信息交流和贪婪选择，将适应度值较优的个体存放到子种群S1中，将适应度值较差的个体存放到子种群S2中。

　　Step7：判断是否达到最大迭代次数，若是，则跳出循环，保存最优解。若否，则跳转到Step3据需执行求解流程。

　　3、 IGWO算法在物流配送中心选址中的应用

　　本文将改进灰狼优化算法(Improved Gray Wolf Optimization,IGWO)用于优化物流配送中心选址模型。IGWO算法中，每一个灰狼个体的每个维度上的解均标志一个配送点，每一个灰狼个体均代表一个所求解，既优化所得配送中心地址。设每一个灰狼个体可表示为X=[x1,x2,?,xN]，其中N为物流配送点。设物流配送中心选址模型中，具有8个配送点，并将在8个配送点中选择3个作为配送中心，若X=[1,0,0,1,1,0,0,0]则表示将第1,4,5个配送点作为配送中心。

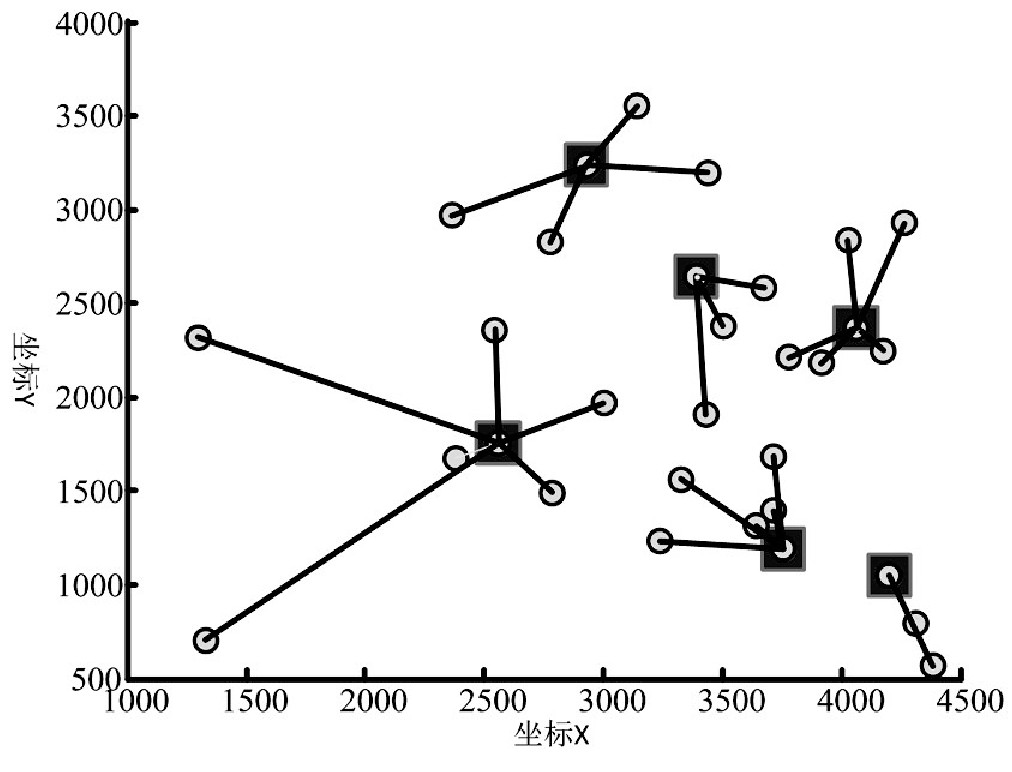
　　为了验证本文所提IGWO算法具有较强的搜索精度和优化能力，可以用于求解物流配送中心选址模型，本文选择30个目标城市的经纬度城市坐标作为配送点，记录其货品需求量，具体信息如表1所示。通过IGWO算法对模型进行求解，将求解结果与改进模拟退火算法的求解结果[4]以及BP人工神经网络算法的求解结果[7]进行对比验证。实验结果如表2、图1、图2和图3所示。BP人工神经网络算法和改进模拟退火算法的算法参数详见文献[7]和文献[4]。三种算法的迭代次数均为100。

　　表1 30个城市的供需点地理位置及供需量

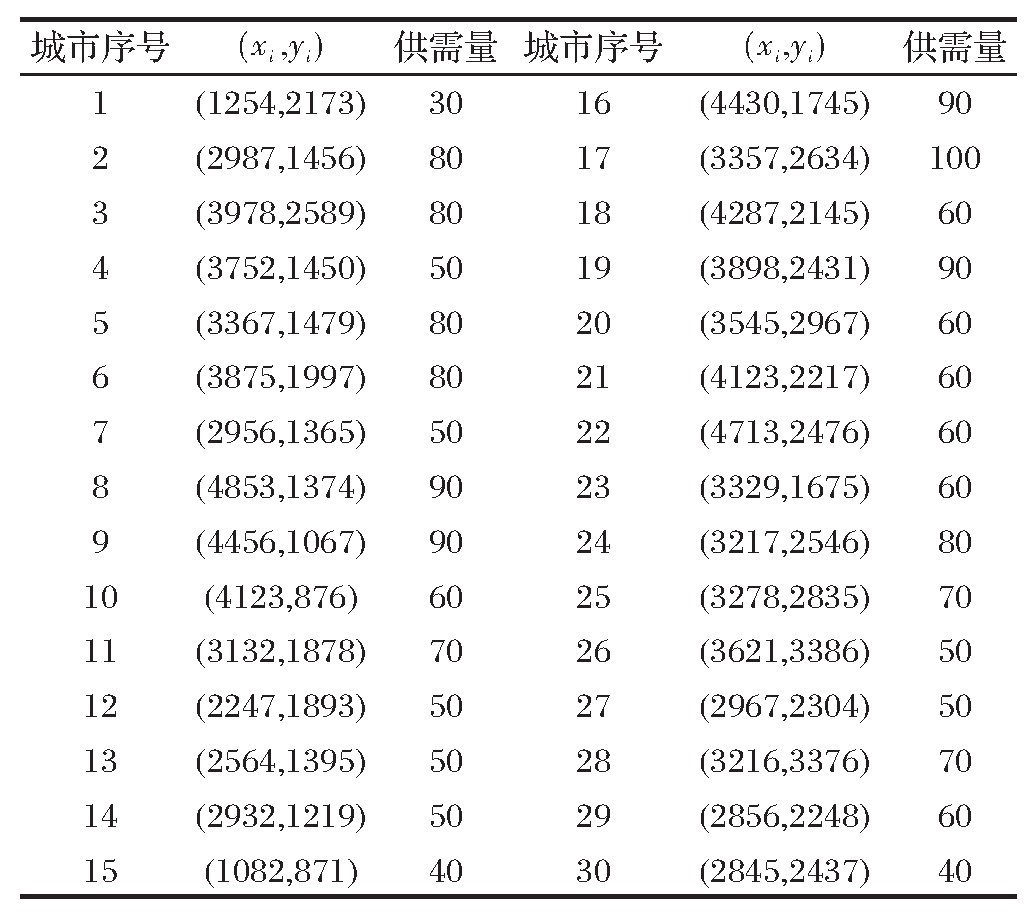
　　表2 4种算法的选址对比结果

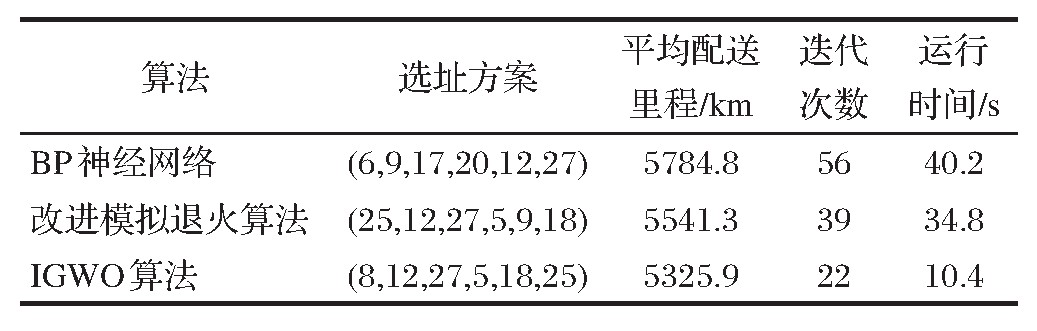
　　图1 基于BP神经网络算法的物流配送中心选址结果

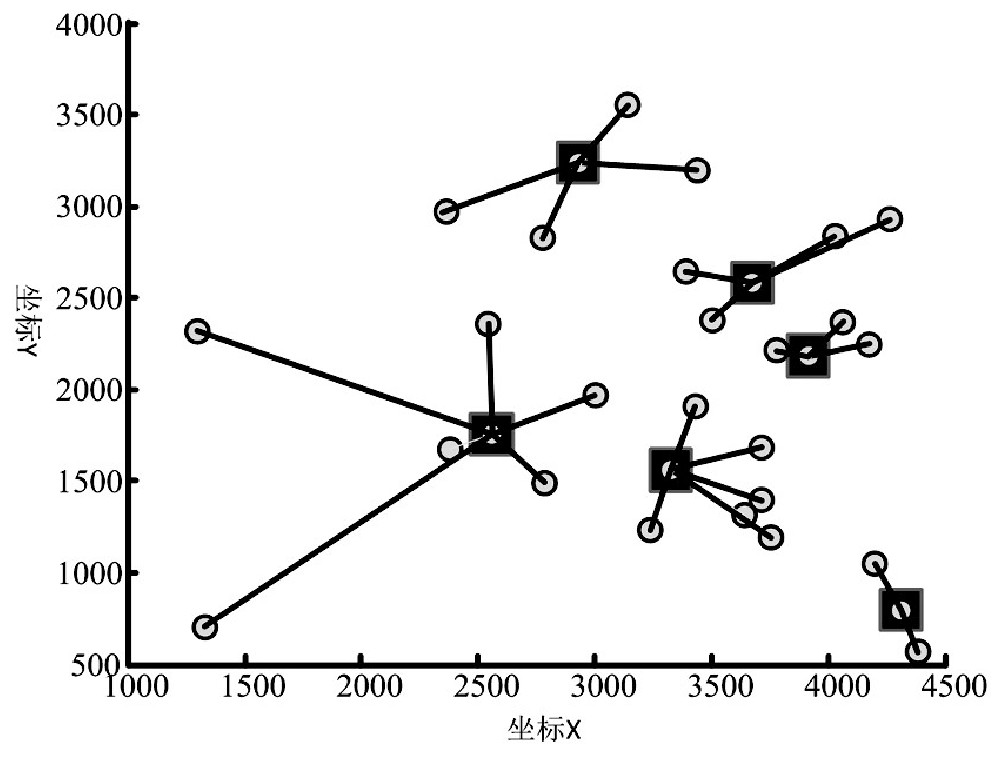
　　从表2、图1、图2和图3的对比求解结果可知，相较其他两种算法的求解结果而言，本文所提改进灰狼优化算法求解的物流配送路径最短，为5325.9KM，说明本文IGWO算法具有较高的收敛精度，求解的配送中心地址，很大程度的降低了配送距离，节约了配送成本，提高了配送效率。此外，通过算法的求解时间可知，本文IGWO算法的求解时间仅为10.4s，并且在第22次迭代可收敛的稳态，说明本文IGWO算法相较其他两种优化算法而言，计算时间最短，算法的初值寻优精度更高，收敛速度更快，更适用于物流配送中心选址模型的计算优化。

　　图2 基于改进模拟退火算法的物流配送中心选址结果

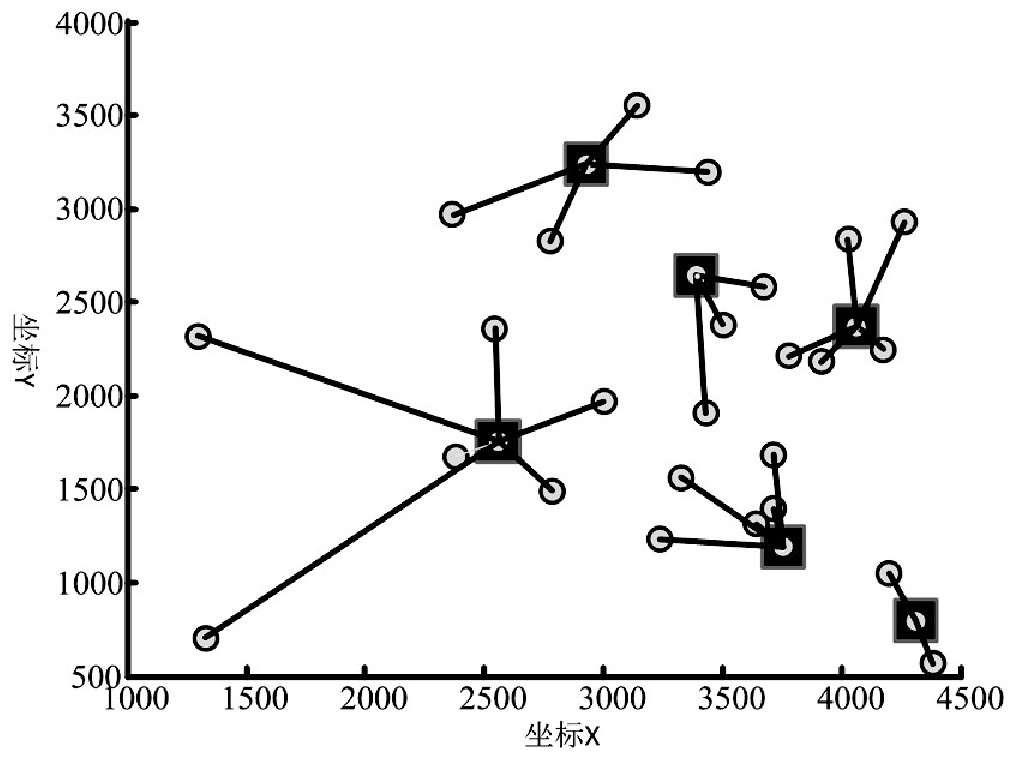
　　图3 基于IGWO算法的物流配送中心选址结果

　　4 结束语

　　本文针对物流配送中心选址模型具有非线性和多约束性能以优化的问题，提出一种改进的灰狼优化算法的求解策略。通过将基本灰狼优化算法与遗产算法相结合，改进后的灰狼优化算法不再通过单一机制进行寻优，并且丰富了算法的种群多样性，提高了算法跳出局部最优的能力。为避免算法在迭代后期陷入寻优停滞，通过双种群策略对算法进行改进，提高了算法的寻优速度。最后将改进的灰狼算法优化物流配送中心选址模型，实验结果证明，IGWO算法很大程度的缩短了配送里程，降低了配送成本，节约了配送时间，这也验证了该算法具有较高的全局搜索精度和优化能力，可以快速的选择出合理的物流配送中心地址。

　　参考文献

　　[1] Zhang Q, Hong L. Location of logistics distribution center with grey demand and grey production capacity based on hybrid PSO [C]/IEEE International Conference on SystemsMan and Cybernetics IEEE,2010.

　　[2] GuanghuaW, Zhanjiang S. Application of AHP and Steiner tree problem in the location-selection of logistics' distribution center[C]/International Conference on Networking andDigital Society. IEEE,2010.

　　[3] Y. Abo-Elnaga and B. El-Sobky and L. AI-Naser. An active-set trust-region algorithm for solving warehouse location problem[J]. Journal of Taibah University for Science,2017.11(2)-:353-358

　　[4]刘婧基于改进模拟退火算法的船舶物流配送中心选址研究[J]舰船科学技术202042(16): 199-201

　　[5]李锐,李晓会.陈鑫可靠性绿色物流配送选址路径问题研究[J.计算机工程与应用,2020 .56(23):237-244

　　[6]吴洋.多目标进化算法在物流配送中心选址中的研究与应用[D].浙江工业大学2020.

　　[7]刘娟.刘祥伟基于改进的BP人工神经网络的物流配送中心选址问题研究[J]喀什大学学报,2018 39(6)-14-19

　　[8]王勇，黄思奇.刘永，许茂增基于K-means聚类方法的物流多配送中心选址优化研究[J].公路交通科技,2020.37(1):141-148

　　[9]向子权杨家其李慧琳梁学恒基于离散灰狼算法的资源分配问题求解[J/OL]华中科技大学学报(自然科学版):1-5[2021-05-07].