神经元作为神经系统的基本结构和功能单位,当受到刺激时会产生一个短暂而急促的尖峰信号,即动作电位,也称锋电位. 神经元间的信息传递就是通过锋电位实现的. 为了解开人脑的学习记忆等诸多谜团,神经元的群体放电模式逐渐成为了生物学界的研究热点之一,而判断每个锋电位是哪类神经元发放的( 即锋电位分类) 过程则是展开这一系列研究的前提.人体内含有成千上万的神经元,不同神经元产生的锋电位具有各自的形态特点,锋电位分类就是根据锋电位各自的形态特点将其归类的[1].目前锋电位分类的主要方法有聚类分析法[1,2],人工神经网络[3,4],模板匹配[5],支持向量机[6-8〗,独立成分分析[9]等,这些方法都是将原始数据作为输入直接进行分类,由于叠加锋电位的存在及噪声的干扰使得分类准确率并不理想. 一些学者在此基础上对原始锋电位数据进行了优化,将原始数据按照一定的规则映射到新的坐标系下重新表示以提高分类效果,目前的优化方法主要有小波变换[10]( Wavelet Transformation) 、主成分分析方法[11-12]( Principal Component Analysis,PCA) 等.将这些优化方法与分类方法相结合在一定程度上能够提高锋电位分类效果,但当锋电位波形相似度较高或含有大量叠加锋电位时,这些方法的分类准确率将会明显降低[13].本文针对不同类型锋电位在各个波峰时刻波形变化趋势不同的特点提出基于二阶差分的锋电位特征表示法,对每一个锋电位波形求取二阶差分,所得的二阶差分序列作为新的特征向量进行分类. 此方法描述出了锋电位波形在各个时刻的变化趋势,并降低了噪声信号的干扰,可有效提高锋电位分类准确率.
1 、基于二阶差分的锋电位特征表示.
1. 1 、锋电位形态特点分析
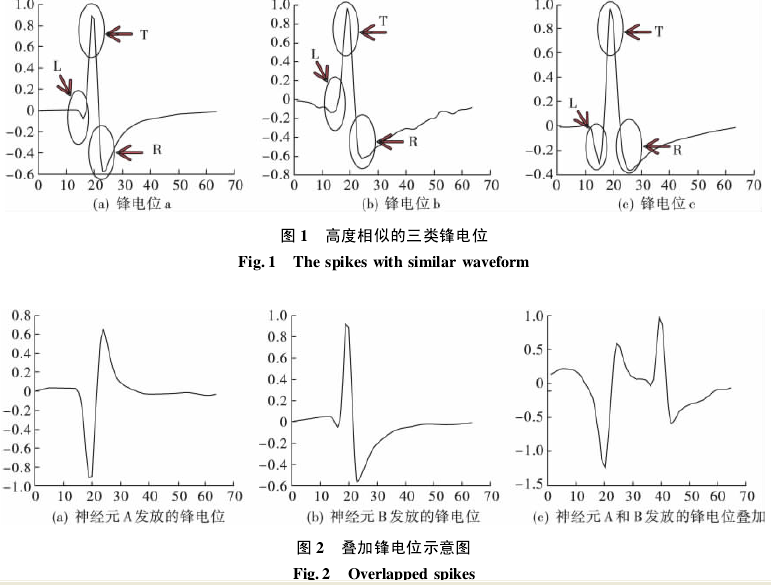
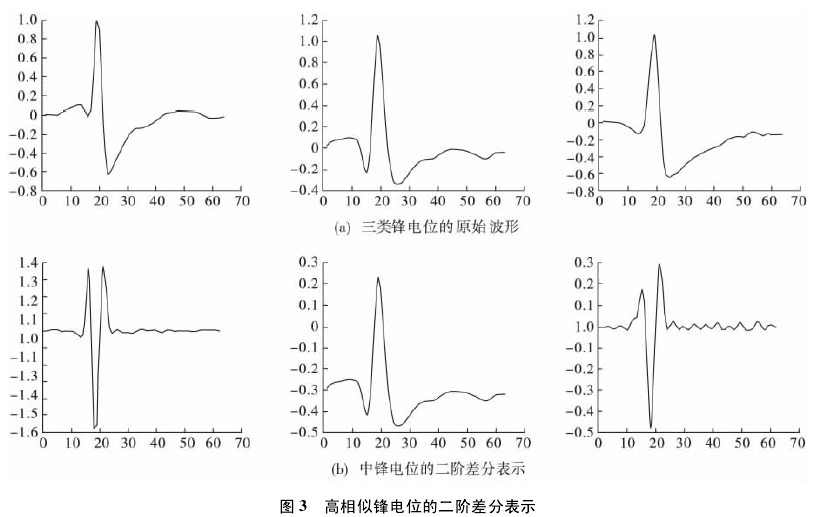
一般情况下,不同神经元产生的锋电位形态是不一样的,但有些情况下不同神经元产生的锋电位形态却极其相似. 当锋电位形态相似度很高时,传统分类方法的分类精确度将有所下降. 经过大量的实验和观察可以看出,虽然不同类型神经元的高度、宽度等特征值相似,但不同类型的神经元产生的锋电位在各个时刻的波形趋势是不一样的,尤其是在锋电位的特征点,如图 1 中标记为 L、T、R 的三段波形幅值变化急剧程度明显不同,而传统的特征表示方法和分类方法无法突出此特点.另外,在多电极采集阵列中,MEA 采集电极周围往往存在着多个神经元,当多于一个的神经元在某一时刻同步放电时,单个采集电极采集到的是多个锋电位的叠加,如图 2( c) 中波形是两个锋电位部分叠加后形成的. 波形的叠加将使锋电位前后信息部分丢失,提高了分类的难度.
1. 2 、二阶差分表示法
锋电位的不同归根结底是因为不同类型的神经元产生的锋电位形态具有差异性,这种差异性可由锋电位在各个时刻的波形趋势表现出来,尤其是在锋电位的特征点处( 我们称其为拐点) . 在数学上差分通常是微分在离散函数中的等效运算,本文用差分来描述锋电位波形的变化趋势,提出基于二阶差分的锋电位特征表示法. 对于函数 f( x) ,如果:
△f( x) = f( x + 1) - f( x) ( 1)则称 △f( x) 为 f( x) 的一阶前向差分( 通常所的差分一般指前向差分) . △n[f]( x) 为 f( x) 的 n 阶差分,如果:
称为二阶差分.假设x = ( x( 0) ,x( 1) ,…,x( m -1) ) 代表一条原始锋电位样本,其中 x( i) ( 0 ≤ i ≤ m - 1) 表示波形任意一点对应的幅值,m 为样本维数. 设 z =( z( 0) ,z( 1) ,…,z( p - 1) ) 表示一条与原始样本相对应的转换后的样本,即对原始波形求二阶差分之后所得的样本向量. 则对于转换后样本的第k维属性值,其计算方法如下所示:
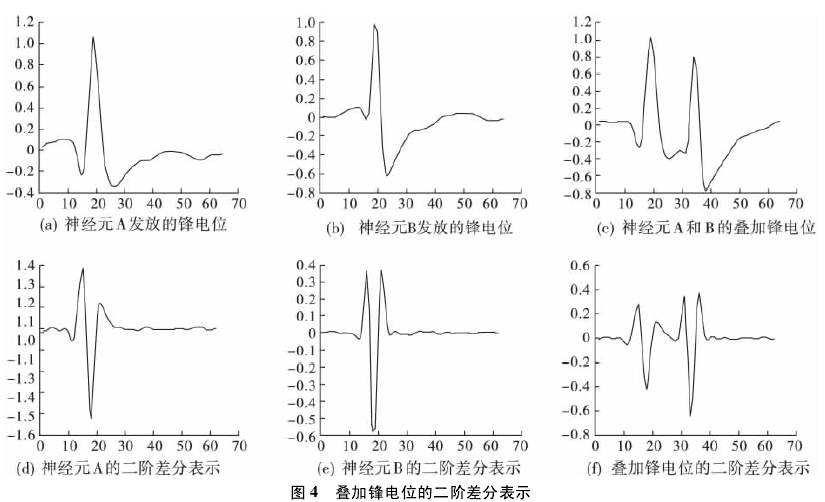
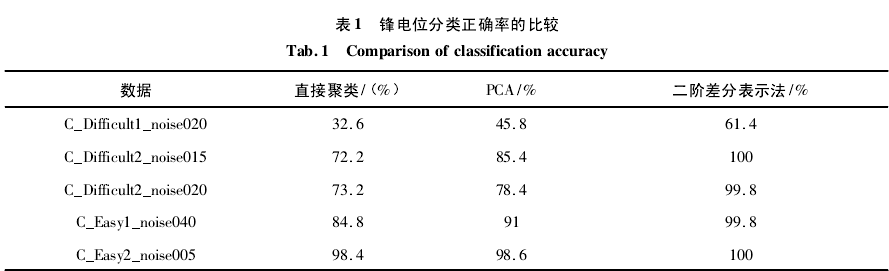
zi( k) = xi( k + 2) - 2xi( k + 1) + xi( k) ( 5)从公式( 5) 可以看出,转换后的样本向量是原始波形的二阶差分序列,能够反映出各个时刻波形的变化趋势. 图3是形态高度相似的锋电位进行二阶差分表示后的效果对比图. 从图中可以看出,样本之间的相似度大大降低. 叠加锋电位的二阶差分表示如图 4 所示. 从图4( c) 和( f) 可以看出,二阶差分表示可以补充叠加锋电位的部分丢失信息,更有利于叠加锋电位的分类.
2 、实 验
本文所用实验数据是来自 Wave_clus 的实验仿真数据,共包括 4 个数据集,每个数据集中包含不同噪声水平作用于三类锋电位的多组数据. 每个数据集中含有 3 200 -3 600 个锋电位( 包含叠加和非叠加波形) .
2. 1 锋电位分类方法.
本文利用二阶差分表示法和 K - means 聚类相结合对锋电位进行分类. 算法思想简述如下:
1) 对原始样本用二阶差分表示法重新表示;2) 给定聚类数目 K,并选择非叠加样本中每一类的第一个样本作为初始聚类中心;3) 对每一样本,计算其与各聚类中心的距离;4) 将该样本归类至与其最近的类别并重新计算此类别聚类中心;5) 重复步骤 3) 和 4) 直至所有样本归类;6) 判断是否达到聚类停止条件,如是则算法结束,否则保留当前聚类中心并返回 3) 对所有样本重新聚类. 其中,聚类停止条件可以是聚类中心不再变化或达到最大迭代次数.
2. 2 实验结果及分析
为了对实验结果进行比较,本文在每个数据集上分别进行了三组实验: 将原始锋电位数据直接进行 K - means 聚类、将原始锋电位用 PCA 方法进行优化后再进行 K - means 聚类、将原始锋电位用二阶差分表示后再进行 K - means 聚类. 部分数据集锋电位分类正确率结果如表 1 所示
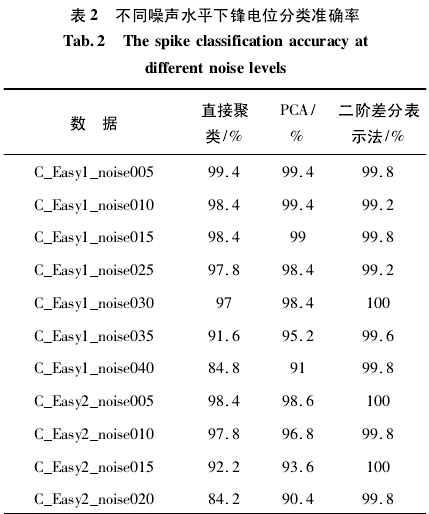
表 1 中各组数据中都含有大量的叠加锋电位.其中,C_Difficult1 和 C_Difficult2 数据中的锋电位样本相似度高,C_Easy2 和 C_Easy1 数据中的锋电位样本相似度较低. noiseXXX 代表各组数据的噪声水平,数值越大代表噪声越大. 从表 1 的实验结果可以看出,与直接用 K - means 聚类和用 PCA 方法优化后聚类相比,二阶差分表示法能提高锋电位分类的准确率,尤其对于锋电位形态相似度极高的 C_Diffi-cult1 和 C_Difficult2 数据,分类准确率提高更明显.为了验证本方法的鲁棒性,我们对同一数据集中不同噪声水平的数据进行了相同的实验,部分实验结果如表 2 所示.
从表 2 可以看出,对 C_Easy1 和 C_Easy2 两组数据直接进行 K - means 聚类和用 PCA 方法优化后再聚类时,随着噪声增大,锋电位分类准确率都有所下降. 基于二阶差分表示法进行锋电位分类,准确率都保持在较高水平,抗噪声能力较强.
3 、结 论.
针对相似度较高的锋电位,分类难度大和由于叠加锋电位造成波形信息丢失、增大分类难度的问题,本文提出了一种新的锋电位特征表示方法 - 二阶差分表示法,利用二阶差分表示法和 K - means 聚类相结合对锋电位进行分类. 实验证明,二阶差分表示法描述出了不同类型锋电位在各个时刻的变化趋势,增大了不同类型锋电位样本间的差异性,能提高形态高度相似的锋电位的分类准确率. 并且,利用二阶差分表示法可以补充由于锋电位叠加而丢失的部分波形信息,有利于提高叠加锋电位分类准确率. 另外,大量实验也表明,本方法在不同信噪比水平下都能保持较高的锋电位分类准确率,具有较强的鲁棒性.
参 考 文 献:
[1] 丁伟东,袁景淇,梁培基. 多电极锋电位信号检测与分类方法研究[J]. 仪器仪表学报,2006,27 ( 12) :1636-1640.
[2] 王 静,封洲燕. 多通道神经元锋电位检测和分类的新方法[J]. 生物化学与生物物理进展,2009 ,36(5) : 641-647.
[3] Gibson S. Comparison of spike sorting algorithmfor futurehardware implementation[J]. Vancouver Brith columbia,Canada 30th Annual International IEEE EMBS Confer-ence,2008( 20 - 24) : 5015 - 5020.
[4] John J W,Liam J McDaid,Jose A Santos,et al. A spikingneural network training algorithm for classification prob-lems[J]. IEEE Transactions on Neural Networks,2010,21( 11) : 1817-1830.
[5] Zhang Pu-ming,Wu Jin-yong,Zhou Yi,et al. Spike sor-ting based on automatic template reconstruction with a par-tial solution to the overlapping problem[J]. Journal ofNeuroscience Methods,2004,135: 55-65
.
[6] Weidong Ding,Jingqi Yuan. Spike sorting based on multi- class support vector machine with superposition resolu-tion[J]. Medical and Biological Engineering and Compu-ting,2008( 46) : 139-145.
[7] 王国胜. 支持向量机的理论与算法研究[D]. 北京: 北京邮电大学,2007.
[8] 李红莲,王春花,袁保宗. 一种改进的支持向量机 NN -SVM[J]. 计算机学报,2003,26( 8) : 1015-1020.
[10]丁 颖,范颖乐,杨 勇. 神经元动作电位模式分类的小波时频分析方法[J]. 计算机应用,2010,30( 10) : 2723-2726.
[12]王冬雪,周逸峰. 基于数学形态学与核主成分分析的锋电位检测与分类方法[J]. 北京生物医学工程,2012,31( 3) : 268-272.[13] Guang-Li Wang,Yi Zhou,Ai-Hua Chen,et al. A robustmethod for spike sorting with automatic overlap decomposi-tion[J]. IEEE Transactions on Biomedical Engineering,2006,53( 6) : 1195-1198.