摘 要: 基于投入产出视角, 运用超越对数随机前沿模型测度2006—2016年长三角城市群创新效率并对其影响因素进行实证检验。结果表明:长三角城市群创新效率总体呈上升趋势, 但各城市间的差异明显, 空间格局变化较大;“中心—外围”格局凸显, 主要以合肥、苏州、杭州、上海为创新核心城市, 向内陆外围城市不断扩散;区域经济发展水平、政府支持力度、对外开放程度及教育水平均对创新效率具有显着的正向影响, 其中政府支持力度影响最显着, 而区域基础设施影响不显着。
关键词: 创新投入产出效率; SFA模型; 长三角城市群;
Abstract: Based on the perspective of input and output, this paper uses the transcendental logarithmic stochastic frontier analysis ( SFA) model to measure the innovation efficiency of city cluster in the Yangtze River delta from 2006 to 2016 and empirically tests its influencing factors. The results show that: ( 1) The innovation efficiency of city cluster in the Yangtze River delta is generally on the rise, but there are obvious differences among cities, and the spatial pattern changes greatly. ( 2) The " center-periphery " pattern is prominent, and Hefei, Suzhou, Hangzhou and Shanghai are the core city for innovation, and the innovations are spread to the inland cities constantly. ( 3) It' s obvious that the innovation efficiency is positively affected by the level of regional economic development, government support, openness to the outside world, and education level, among which the government support has the most significant impact but the effect of the regional infrastructure remains the least.
Keyword: innovation input-output efficiency; SFA model; city cluster in the Yangtze River delta;
在新常态经济背景下, 创新资源是国家的核心竞争力。2016年3月, 《国民经济和社会发展第十三个五年规划纲要》提出, 以城市群为主体发展形态, 坚持以创新驱动发展战略为目标。为提升区域经济发展水平, 带动长江流域甚至全国经济发展, 最终实现我国创新型国家建设, 迫切需要提升长三角城市群的创新能力, 特别是创新效率。

对区域创新效率的相关研究主要包括创新效率的测度和影响因素分析这两大方面。创新效率测度的主流方法有两类:一类是参数方法, 主要是随机前沿方法 (SFA) ;另一类是非参数方法———数据包络分析法 (DEA) 。SFA主要是以C—D生产函数[1]和超越对数生产函数[2]为模型测度创新效率, 同时对其影响因素进行实证检验。运用DEA测度创新效率的研究成果也很丰硕, 研究范围主要涉及省域层面[3]、行业层面[[4,5]-5]、企业层面[6]等。在影响因素分析方面, 主要运用DEA-Tobit模型和随机前沿分析模型进一步分析创新效率的影响因素。总体来说, 虽然创新效率研究成果颇多, 但依然存在不足:创新效率的研究主要基于省域、行业、企业层面, 对城市群及各地级市创新效率的研究极少;创新效率测度方法具有一定的局限性, 比如DEA方法不能准确分离技术非效率和随机误差的影响, 且不能直接分析创新效率的影响因素, 一般需要借助Tobit模型对影响因素进行分析。为了解决DEA方法的局限性, SFA模型除了能够对参数进行检验以外, 还能区分技术非效率和随机误差的影响, 能一步到位实现创新效率和影响因素分析。同时, 运用Arc-gis方法探索创新效率的空间差异情况, 找准关键影响因素。
一、长三角城市群创新效率测度分析
(一) 创新投入产出现状
1. 创新活动投入
首先, 在创新人力资源投入方面, 2016年, 上海、江苏、浙江、安徽R&D人员达到254800、481093、330929、158289人。1上海共有普通高等学校64所, 在校学生51.47万人, 同比增长0.6%。江苏省共有普通高等学校141所, 在校学生190.74万人, 国家及省级重点实验室170个, 科技服务平台294个, 创新发展研究中心3126个。浙江省共有普通高校108所, 在校学生99.61万人。安徽省共有普通高校109所, 在校学生114.5万人, 专业技术人员224.6万人, 较上年增长1.9%。 (2)
图1 2006—2016年长江三角洲城市群R&D经费投入情况
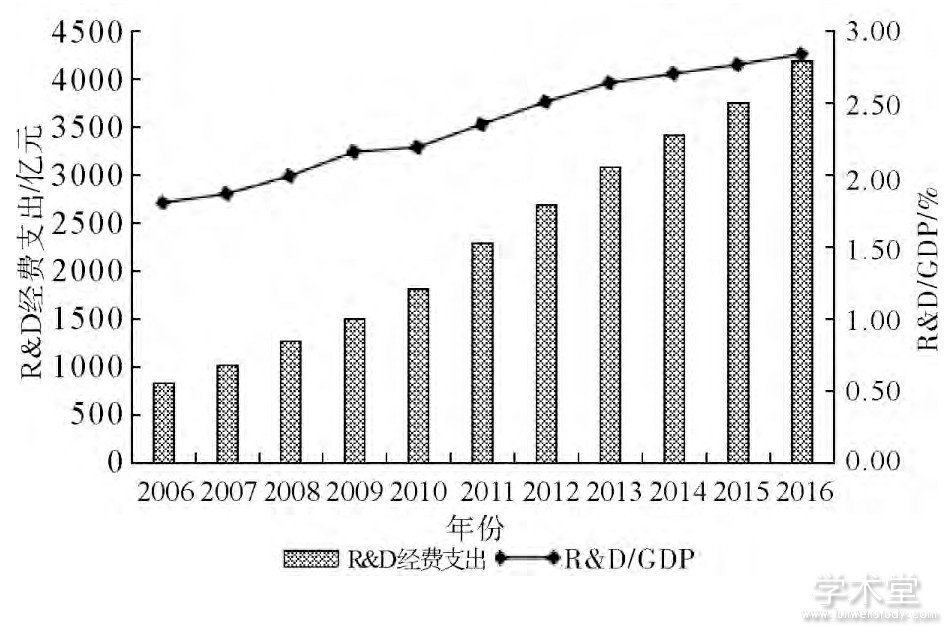
数据来源:2007—2017年上海市、江苏省、浙江省、安徽省统计年鉴
其次, 在资金投入方面, 2016年, 上海、江苏、浙江、安徽R&D经费支出分别为1049.32亿元、1749亿元、996.4亿元、389亿元, R&D投入强度, 即R&D经费支出占GDP比值分别为3.72%、2.7%、2.51%、2.43%, 均超过了2%。 (1) 从图1来看, 2006—2016年长江三角洲城市群R&D经费投入、R&D经费投入强度均呈逐年增长态势。
2. 创新活动产出
随着创新环境的不断优化, 长江三角洲城市群创新活动产出水平逐年上升。上海市2016年专利申请、授权量分别为119937件、64230件, 同比增长19.93%、5.95%;年末共认定高新技术成果转化项目10969项, 实现技术合同成交额822.86亿元, 同比增长16.2%。江苏省2016年技术合同成交额728亿元, 同上年相比增长4.0%。浙江省2016年专利申请数量39.3万件, 发明专利授权量2.7万件, 同比增长13.8%。安徽省2016年受理申请专利172552件, 授权专利60982件, 比上年分别增长35.1%和3.3%。 (2) 图2反映了长江三角洲城市群2006—2016年专利申请及授权情况, 大体来说, 专利申请及授权的数量呈逐年增长的趋势。
(二) 构建创新效率测度模型
SFA模型最初由Aigner等提出[7], 随后Battese和Coelli等对其进行拓展和完善, 提高了随机前沿模型的灵活性和适用性, 此后被应用到对技术创新效率的评价[8]。SFA模型有两种生产函数形式, 即柯布—道格拉斯生产函数 (C—D函数) 和超越对数生产函数 (Translog生产函数) 。C—D函数不考虑技术进步和假定产出弹性恒定, 而Translog生产函数的约束条件较少, 使用灵活, 能减少函数形式带来的偏差。因为模型的设定方式将直接影响效率值估计的真实性, 所以分别设定两个模型, 以便区分模型的真实性。根据C—D生产函数建立的第一个模型如下:
图2 2006—2016年长江三角洲城市群专利申请、授权情况

数据来源:2007—2017年上海市、江苏省、浙江省、安徽省统计年鉴
其中i, t分别表示城市和年份;α0为常数项;α为模型待估参数;Vit为随机误差项, 服从N (0, σv2) ;Uit为技术非效率项, 反映技术无效率的程度, 服从N (u, σu2) , u为非负, 且Vit和Uit相互独立。
基于Translog生产函数建立的第二个随机前沿分析模型如下:
式 (2) 2中β为待估参数, Vit和Uit的含义同模型 (1) 3。
式 (3) 中TEit表示科技创新效率水平。当TEit=1时, 即实际产出与最大产出是相等的, 科技创新投入有效;当TEit=0时, 科技创新投入无效。
式 (4) 是创新非效率模型, 其中Zit为创新效率的影响因素, δ为创新效率影响因素的待估系数, Uit为科技创新非效率项, Uit越大, 表示科技创新效率越低, 即投入等量的创新资源转化的创新产出越少。
式 (5) 中γ用于检验创新技术无效占总误差项的比重, 若原假设γ=0被接受, 则表明估计结果的偏离全部来自于随机误差项, 此时使用传统最小二乘估计即可。如果γ通过广义似然比检验, 大于0接近1时, 说明样本数据更适合用SFA模型分析。
(三) 创新效率评价指标体系设计及数据来源
对于创新投入指标的选择, 本研究在全面考虑指标选取的代表性、适当性、有效性等基本原则上, 选取了R&D人数和R&D经费内部支出两个指标, 分别从人力和财力两方面反映创新要素的投入。创新产出指标一般可分为知识产出和经济产出。结合已有研究, 综合数据可得性, 选用专利授权量衡量知识产出;经济产出指标一般包括新产品销售收入、高新技术产业值等, 由于新产品销售收入数据无法统一, 所以本研究采用高新技术产业值衡量区域创新带来的经济产出。基于以上投入产出变量, 建立创新评价指标体系如表1所示。
表1 城市创新效率评价指标体系

考虑到价格因素的影响, 以2006年为基期, 利用CPI价格指数对R&D经费支出及高新技术产业值指标进行平减。考虑到创新产出存在时滞, 大多学者证实一般为1年。因此, 投入指标对应2006—2015年数据, 产出指标对应2007—2016年数据。各评价指标数据均来源于2007—2017年的上海、江苏、浙江、安徽等省 (直辖市) 统计局、各地级市统计年鉴、《江苏科技统计年鉴》《浙江科技统计年鉴》《上海科技统计年鉴》及《中国城市统计年鉴》和相应的政府门户网站。部分缺失数据按照插值法补齐。
(四) 模型检验及结果分析
在进行效率测度前, 需要检验是采用柯布—道格拉斯生产函数还是超越对数生产函数的SFA模型, 检验标准是广义似然比统计量λ=-2ln[L (H0) /L (H1) ][9]。其中, L (H0) 是受约束的原假设LOG函数值, L (H1) 是不受约束的备择假设LOG函数值。若λ小于临界值, 则接受原假设;反之, 则拒绝原假设, 使用超越对数生产函数模型进行估计。
表2给出了不考虑效率影响因素下参数估计结果, 不同产出指标下的γ值在1%显着性水平下均显着, 反映技术非效率项显着存在, 此时SFA模型比OLS模型要更适合。另外, β3、β4、β5均在1%显着性水平下不为0, λ也显着通过似然比检验, 表明样本数据更适合采用超越对数生产函数的SFA模型来测算。
1. 历年创新效率估计结果
基于表2和表3的结果, 本研究最终选用超越对数生产函数形式的SFA模型, 通过Frontier 4.1软件测算出的长江三角洲城市群历年创新效率值如图3所示。
表2 SFA模型参数估计结果

注:括号内表示t值, *、**、***分别表示在10%、5%、1%水平下显着。临界值是在1%显着性水平下的值, 原假设即C—D生产函数形式的随机前沿分析模型
图3 2007—2016年长三角城市群创新效率变动情况
其中, IE1是以高新技术产业值为产出的创新效率值, 年平均创新效率值为0.781。IE2是以专利授权量为产出的创新效率值, 年平均创新效率值为0.760。不管是IE1还是IE2, 创新效率都呈增长趋势。在2013年前, IE1明显高于IE2, 这是因为高技术产业较专利在短期能更快获得收益, 然而长期来看, 专利产出的创新效率值会比高技术产业的创新效率值高。
2. 各城市创新效率测度结果
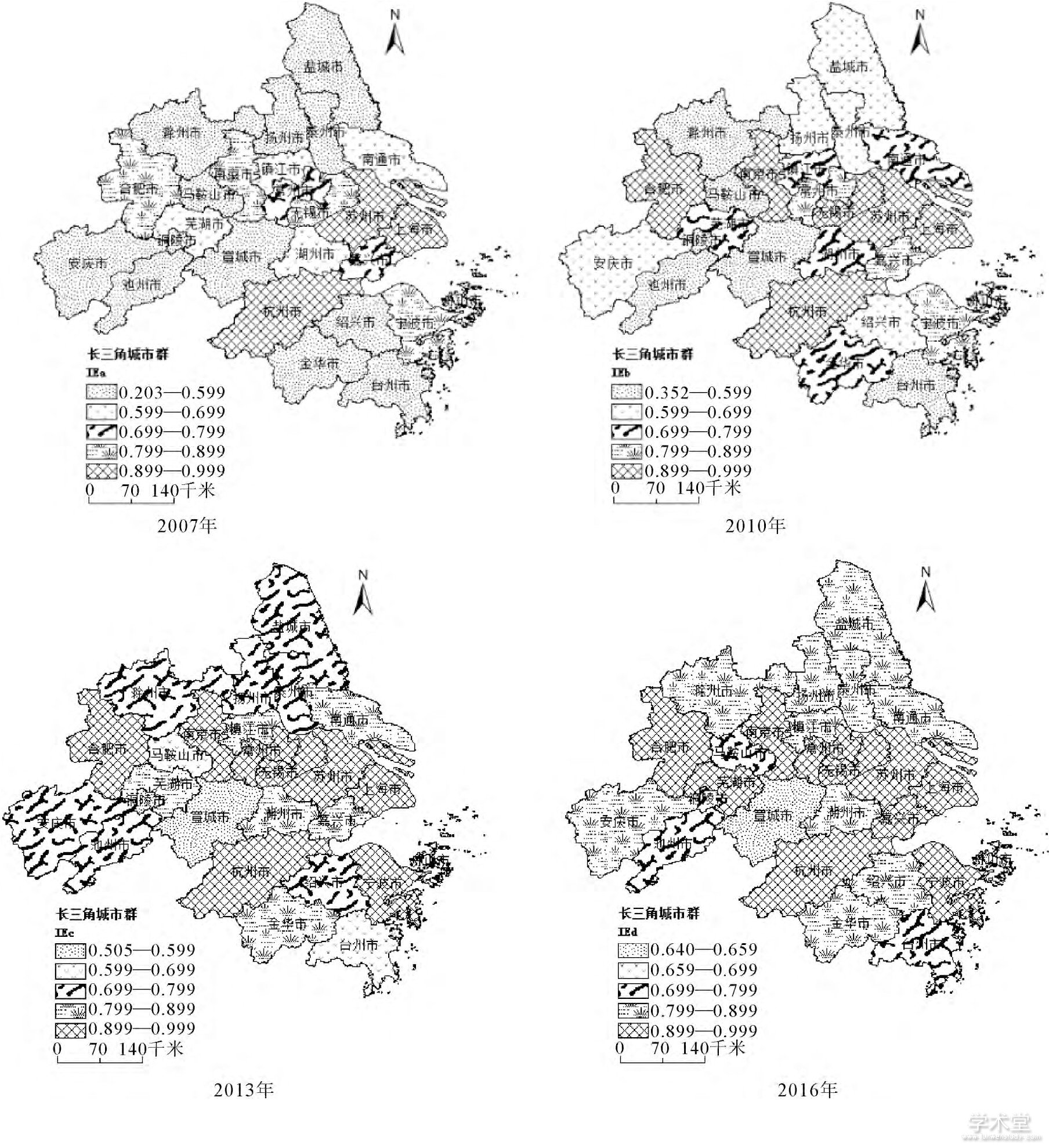
为了了解长江三角洲城市群创新效率的空间差异情况, 以两年为间隔选取2007、2010、2013、2016年各城市创新效率值, 通过Arcgis软件绘制创新效率空间分布图进行对比分析 (以高技术产业值、专利授权量为产出的创新效率图分别见图4、图5) , 能更加直观地找出各城市创新效率水平的差异。
从图4来看, 各城市创新效率水平都在逐年提升, 各城市创新效率空间差异明显, 空间格局变化较大。对比分析2007年和2010年, 创新效率值在0.899以上的有两个城市, 即苏州和合肥;创新效率值在0.599以下的城市有5个, 包括镇江、嘉兴、金华、台州和舟山, 这些城市的创新效率水平还有很大的提升空间。创新效率值在0.699以上的城市数量在逐渐增加, 包括盐城、马鞍山、宣城、湖州、安庆等城市, 因为这些城市距离合肥和苏州比较近, 受到的辐射较多, 创新效率水平提高得也快, 这也从侧面反映了创新效率的空间扩散与城市之间的距离是成正比的。2013年和2016年, 整体的创新效率水平有了很大的提升, 尤其是以合肥、苏州、杭州、上海为创新中心的城市, 向内陆城市不断扩散的趋势很明显;2013年效率值在0.699—0.799区间内的城市在2016年都进步到0.799—0.899这个区间, 说明空间差距在不断缩小。
图4 2007、2010、2013、2016年以高技术产业值为产出的创新效率图

图5是以专利授权量为产出的创新效率空间差异分布图。以专利授权量为产出的创新效率整体呈现增长态势, 但是空间差异明显, 两极分化比较严重, 效率值高的主要有上海、苏州、杭州, 是扩容前两省一市的主要创新中心, 随着安徽省一部分地级市的加入, 合肥市也步入创新中心城市。
图5 2007、2010、2013、2016年以专利授权量为产出的创新效率图
2007年, 有11个城市的效率值在0.599以下, 整体创新水平较低, 但是到2010年, 创新效率值在0.599以下的主要是安徽省的部分城市, 包括滁州、马鞍山、铜陵、池州、宣城等, 数量减少了一半。2013年, 两极分化的趋势明显降低, 除了台州、宣城和铜陵, 其他城市效率值都在0.699以上, 主要是因为这几个城市本身创新能力相对较弱, 加之离各省份创新中心城市较远, 受到的辐射较少, 所以其创新效率水平提升缓慢。2016年, 有21个城市的效率值都在0.799以上, 空间差异在不断缩小, 创新效率也从中心城市不断向外围扩散。
二、影响因素分析
(一) 变量选择及数据来源
参考已有创新效率影响因素研究, 结合数据的可得性, 选择5个关键因素作为长三角城市群创新效率的影响因素变量。一是经济发展水平 (agdp) :采用各市的人均GDP数据衡量经济发达程度;二是政府支持力度 (gov) :选取各市财政支出中科技支出占财政支出的比重, 体现政府对科技创新的支持程度;三是对外开放程度 (fdi) :采用各市实际利用外资额占当地GDP的比重;四是区域基础设施 (inf) :采用邮电业务总量占GDP的比重;五是教育水平 (edu) :采用教育支出占GDP的比重。基于以上变量可构建创新效率影响因素模型如下:
数据来源于2007—2016年《中国城市统计年鉴》, 实际利用外资采用年平均汇率换算成人民币, 为消除价格因素的影响, 采用2006年居民消费价格指数对人均GDP进行平减。
(二) 影响因素实证检验
为了进一步分析创新效率的非效率原因, 探索创新效率的关键影响因素, 运用Frontier 4.1软件对创新效率影响因素进行估计, 结果见表3。
表3 效率影响因素估计结果

注:*、**、***分别表示在10%、5%、1%水平下显着, 括号内为标准差
由表3的相关数值可以看出:
第一, 针对Y1 (高新技术产业值) , 各影响因素存在显着差异, 其中经济发展水平、政府支持力度及对外开放程度对创新效率的影响均至少在5%水平下显着, 而区域基础设施和教育水平均不显着。在通过显着性检验的因素中, 对外开放程度对创新效率的影响最突出, 实际利用外资占GDP比值每提高1%, 创新效率水平将提升3.346%;其次是政府支持力度, 政府科技支出占财政支出的比值每提高1%, 将正向促进创新效率水平提升2.402%;影响最弱的是经济发展水平, 每个区域的人均gdp每增加1%, 创新效率水平将提升1.229%。区域基础设施不能促进创新效率水平的提升, 主要是因为区域基础设施不具有排他性, 随着城市之间的交通越来越便利, 区域基础设施的影响变得不再显着。教育水平对创新效率的影响不显着, 可能是因为教育支出投入还不够, 产出水平较低, 所以对创新效率的影响还不显着。
第二, 从Y2 (专利授权量) 估计结果来看, 各影响因素差异明显, 其中经济发展水平、政府支持力度、教育水平及对外开放程度对创新效率的影响均至少在10%水平下显着, 而区域基础设施均不显着。在通过检验的因素中, 政府支持力度最为显着, 政府科技支出占财政支出的比值每提高1%, 创新效率水平将提升4.777%;对外开放程度对创新效率作用方向为负, 实际利用外资占GDP比值每增加1%, 创新效率水平将会下降2.197%, 主要是因为外商直接投资企业大都是外国企业, 对专利核心技术使用权排他性较强, 所以实际利用外资越多, 对外国专利技术依赖性越强, 反而不利于创新效率水平的提升;教育水平和经济发展水平对创新效率的估计系数分别为-1.504、-1.423, 在1%、10%水平下显着, 表明教育水平及经济发达程度越高的地方, 创新效率水平也会得到提升, 这主要是因为这些城市发展基础较好, 同时注重教育资源投入, 所以科技创新能力会提高。
三、结论和政策建议
以长三角城市群26个城市为例, 基于2006—2016年创新投入产出数据, 对长三角城市群创新投入、产出现状进行描述性分析, 构建创新效率评价指标体系, 并运用SFA-超越对数生产函数模型测算长三角城市群各城市创新效率, 然后进一步对创新效率的影响因素进行分析, 得出以下结论:
一是长三角城市群创新效率整体呈增长态势, 各城市间创新效率差异明显, 空间格局变化较大, 但各城市创新效率差异程度逐渐缩小。根据各城市创新效率情况, 无论是以高新技术产业值为产出的创新效率还是以专利授权量为产出的创新效率估计结果, 都明显呈现“中心—外围”格局, 中心城市包括合肥、苏州、杭州、上海, 外围城市包括台州、宣城、铜陵、池州、安庆等, 中心城市向外围创新能力较低的城市不断扩散的趋势明显。
二是影响因素回归结果显示, 各解释变量对城市创新效率影响程度存在明显差异。以高新技术产业值为产出的创新效率与区域基础设施、教育水平无相关关系, 与政府支持力度、经济发展水平、对外开放程度均呈正相关关系;以专利授权量为产出的创新效率与经济发展水平、政府支持力度、教育水平呈正相关关系, 与对外开放程度呈负相关关系, 区域基础设施影响不显着。
根据上述结论, 本研究重点从两方面提出提升长三角城市群城市创新效率水平的政策建议。
一是各地政府应因地制宜地投入创新资源, 优化区域创新环境。各地政府在加大投入创新资源的同时, 更应该关注创新投入的质量;要落实创新发展的政策, 优化创新环境, 加大科技、教育支出在一般预算支出中的比例, 因为从效率影响因素的估计结果来看, 科技、教育资金的投入对创新效率促进作用明显, 是提升创新能力的重要影响因素。
二是优化长三角城市群创新发展“中心—外围”的空间格局, 缩小各城市创新发展的空间差距。巩固以苏州、上海、杭州为创新核心城市的地位, 同时充分利用国家颁布的相关政策, 重点培育南京、合肥等长三角城市群创新发展的“副核心”, 带动台州、宣城、马鞍山、池州、安庆等“边缘区”的创新发展。
参考文献:
[1]王艳, 龚新蜀, 李津津.基于SFA模型的新疆装备制造业技术创新效率及影响因素分析[J].科技管理研究, 2017 (12) :146-151.
[2]马晓琳, 万志芳.基于随机前沿分析的工业科技创新效率测度[J].统计与决策, 2017 (3) :156-159.
[3]刘明广.区域创新系统的创新效率动态评价———基于省级面板数据的实证研究[J].科技管理研究, 2015 (1) :70-76.
[4]桂黄宝.我国高技术产业创新效率及其影响因素空间计量分析[J].经济地理, 2014 (6) :100-107.
[5]谢子远, 吴丽娟.产业集聚水平与中国工业企业创新效率———基于20个工业行业2000—2012年面板数据的实证研究[J].科研管理, 2017 (1) :91-99.
[6]陈兴海, 王诤诤, 鲁文霞.上海科创引擎企业驱动全球科创中心发展创新效率测度———基于DEA-Tobit模型的实证分析[J].科技管理研究, 2016 (10) :61-65.
[7] AIGNER D, LOVELL C, SCHMIDT P. Formulation and estimation of stochastic frontier production function models[J]. Journal of Econometrics, 1977 (1) :87-99.
[8]周姣, 赵敏.我国高新技术产业开发区创新效率及其影响因素的实证研究[J].科技管理研究, 2014 (10) :1-6.
[9]李向东, 李南, 刘东皇.高技术产业创新效率影响因素分析[J].统计与决策, 2015 (6) :109-113.
注释:
1 相关数据来源于2017年上海市、江苏省、浙江省、安徽省统计年鉴。
2 相关数据来源于2016年上海市、江苏省、浙江省、安徽省统计公报。
3 (2) 相关数据来源于2017年上海市、江苏省、浙江省、安徽省统计年鉴。