SPSS软件下多水平资料的线性混合模型分析

　　方差分析、线性回归分析、Logistic回归分析等统计方法一般要求数据具有独立性，但在实际工作中，许多数据并不符合"独立性"要求，而具有层次性。例如，学生来自不同的学校，由于生源、教育资源等不同，同一所学校的学生特征（如学习成绩）更具相似性，而不具有独立性，即学生为低层（水平1），学校为高层（水平2），又如纵向数据，同一观察对象的测量资料往往具有相关性，也不具有独立性，即测量时间点为低层（水平1），观察对象为高层（水平2）。上述具有层次结构的资料被称为多水平资料。多水平模型是20世纪80年代初针对多水平资料非独立性问题发展起来的一类模型，根据不同起源、从事的领域、用途和传承等，又被称为混合效应模型、多层次模型、随机效应模型、随机系数模型和方差成分模型等[1,2,3,4].也有研究者将广义估计方程归入多水平模型[2].

　　以学生入学成绩对会考成绩的影响研究为例，基础的二水平模型可描述为：

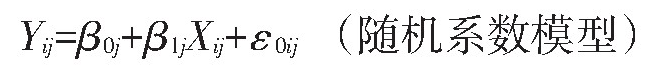
　　式中：因变量Yij为第j所学校第i个学生的会考成绩；自变量Xij为第j所学校第i个学生的入学成绩；ε0ij为学生水平（水平1）的随机误差；β0j为第j所学校截距，可分解为平均截距和第j所学校截距与之离差值（β0+u0j）；β1j为第j所学校斜率，可分解为平均斜率和第j所学校斜率与之离差值（β1+u1j）。当方差Var （u1j）假设为0成立时，即各学校的斜率相同，模型简化为：

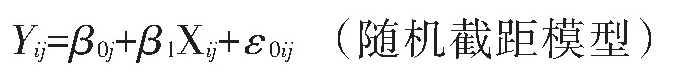
　　当方差Var （u0j）假设为0成立时，即各学校截距也相同，说明数据具有独立性，模型可进一步简化为一般线性模型。

　　为方便说明，采用因变量为连续变量，单自变量资料介绍多水平模型，以及模型由繁到简演化的条件，但多水平模型多用于分析含多个自变量的资料。利用连接函数，多水平模型也可分析因变量为离散型数据的资料，如多水平Logistic回归分析。下面举例介绍SPSS 21.0软件实现线性混合模型分析多水平资料的过程。

　　1 案例

　　1.1 资料

　　某研究分析65所学校4 059名学生入学成绩对会考成绩的影响[2],SPSS 21.0软件数据录入格式见表1,其中会考成绩和入学成绩均已进行标准正态变换。

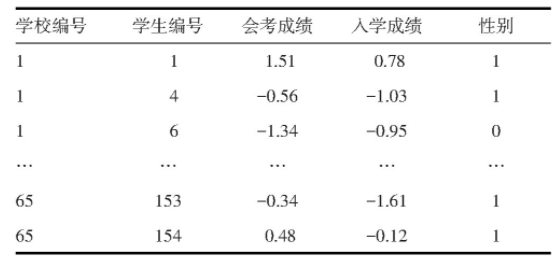
　　表1 学生成绩数据

　　1.2 SPSS软件操作说明

　　选择"分析""混合模型""线性";

　　将"学校编号"选入"主题"列表框，单击"继续"按钮；

　　将"会考成绩"选入"因变量"列表框，将"入学成绩"选入"协变量"列表框，将"性别"选入"因子"列表框；

　　单击"固定"按钮，进入固定效应选择面板；将"入学成绩""性别"选入"模型"列表框，单击"继续"按钮；

　　单击"随机"按钮，进入随机效应选择面板；选择"包括截距"选项，将"入学成绩"选入"模型"列表框，将"学校编号"选入"组合"列表框，单击"继续"按钮；

　　单击"统计量"按钮，进入统计量选择面板；选择"参数估计"和"协方差参数检验"选项，单击"继续"按钮；

　　单击"确定"按钮。

　　1.3 结果描述

　　表2和表3为固定效应分析结果，其格式和结果解释与一般线性模型一致。固定效应检验结果显示，学生的入学成绩和性别对会考成绩均有影响（P<0.05），见表2.参数估计进一步显示，男生会考成绩较女生差（β=-0.173,P<0.05），入学成绩越高则会考成绩越高（β=0.553,P<0.05），见表3.

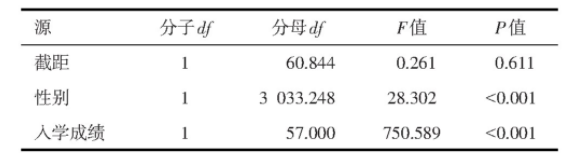
　　表2 固定效应的检验类型Ⅲ

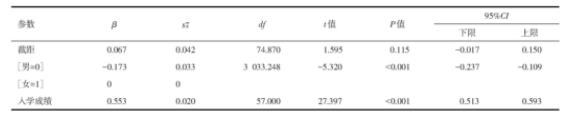
　　表3 固定效应估计

　　表4列出随机效应的检验结果。残差为水平1随机误差，方差有统计学意义说明学生个体成绩存在差异。水平2（学校水平）截距和入学成绩随机误差（斜率）的方差均有统计学意义（P<0.05,即方差为0的假设不成立）。截距不同说明入学成绩=0时（经标准正态变换，相当于入学考试总平均成绩），各学校截距（会考平均成绩）存在差异。斜率不同说明各学校会考成绩受入学成绩的影响程度存在差异。

　　表4 协方差参数估计

　　2 注意事项

　　SPSS统计软件提供了线性混合模型和广义线性混合模型用于多水平数据分析。但是线性混合模型只能分析因变量为连续型的资料；广义线性混合模型可分析因变量为连续型和离散型的资料，但对计算机性能要求较高。与广义线性模型相同，广义线性混合模型可分析正态分布、二项分布、多项分布、指数分布、Poisson分布、Gamma分布、负二项分布等指数分布族资料[2,4].

　　多水平模型的一项重要应用是对重复测量资料的分析。重复测量资料的方差分析要求资料为连续型，完全均衡，满足正态性要求，无法处理有缺失值的资料。而多水平模型能分析非均衡分布含缺失值的资料，能处理连续型和离散型资料，有较多优势。

　　参考文献

　　[1] 孙振球，徐勇勇。医学统计学[M].4版。北京：人民卫生出版社，2016.

　　[2] 张文彤，董伟。SPSS统计分析高级教程[M].3版。北京：高等教育出版社，2018.

　　[3] 杨珉，李晓松。医学和公共卫生研究常用多水平统计模型[M].北京：北京大学医学出版社，2007.

　　[4] 郭伯良。多水平模型应用[M].北京：北京师范大学出版社，2020.