Chen混沌系统的镇定控制及同步控制的实现

　　摘要：对于Chen混沌系统，只采用一个控制器进行系统的镇定控制。通过Chen混沌系统的状态方程，建立同步误差系统，只采用一个控制器进行Chen混沌的同步控制。采用MatLab语言编写程序，进行数值仿真实验。数值仿真结果表明，设计的控制器能够进行Chen混沌系统的镇定控制和同步控制，控制器比较简单，容易实现。

　　关键词：Chen混沌系统； 数值仿真； MatLab; 仿真实验；

　　Abstract:For Chen chaotic system,only one controller is used to stabilize the system.Based on the state equation of Chen chaotic system,the synchronization error system is established,and only one controller is used for synchronization control of Chen chaotic system.The program is written using MatLab language,and the numerical simulation experiment is carried out.The numerical simulation results show that the designed controller can stabilize and synchronize Chen chaotic system.The controller is simple and easy to implement.

　　Keyword:Chen chaotic system; numerical simulation; MatLab; simulation experiment;

　　混沌系统具有丰富且复杂的非线性动力学行为，对初始值非常敏感。混沌理论可以用于信号处理、保密通信、图像加密和混沌电路等多个领域[1,2].混沌控制与同步始终是非线性科学领域的一个热点问题。1999年，陈关荣等[3]在Lorenz系统的基础上，利用工程反馈控制的方法构造了三维自治混沌系统，即Chen混沌系统。Chen混沌系统能够采用硬件电路实现[4].张国山等[5]在Chen混沌系统的第一个方程中加入乘积项，构造了一个新的三维自治混沌系统；胡春华等[6]基于Chen混沌设计了自动切换混沌系统；李德奎等[7]提出单参数Chen混沌系统，并采用硬件电路实现。

　　Chen混沌系统具有复杂的动力学行为，能够采用硬件电路实现，可用于保密通信。本文根据Chen混沌系统的状态方程，设计控制器进行Chen混沌系统的镇定控制和同步控制。采用MatLab语言编写脚本程序进行数值仿真。在脚本程序中，采用四阶-五阶龙格库塔方法（ode45函数）求解常微分方程。数值仿真结果表明，设计的控制器能够实现Chen混沌系统的镇定控制和同步控制，控制器比较简单，容易实现。

　　1 Chen混沌系统

　　1963年，气象学家Lorenz发现第一个混沌吸引子，即Lorenz吸引子。混沌系统具有伪随机性，对初始值非常敏感，可以用于保密通信和信息加密等工程领域。1999年，美国休斯敦大学陈关荣教授发现了Chen混沌系统。Chen混沌与Lorenz混沌类似，但不拓扑等价而且更复杂。Chen混沌系统的状态方程表示为：

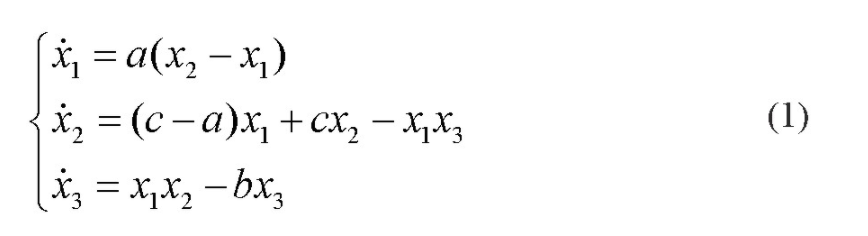
　　其中，x1,x2和x3为Chen混沌系统的状态变量，a,b和c为常数。当a=35,b=3,c=28时，该系统为混沌状态。根据Chen混沌系统的状态方程，采用四阶-五阶龙格库塔方法（ode45函数）进行系统的建模仿真。Chen混沌系统的初始状态设定为x1（0）=2,x2（0）=3,x3（0）=10,步长为0.001秒，仿真时间为40秒。采用MatLab语言进行Chen混沌系统仿真的脚本程序为：

　　脚本程序进行Chen混沌系统的数值仿真，程序运行后，Chen混沌系统的吸引子如图1所示。

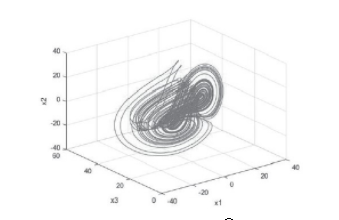
　　图1 Chen混沌系统的吸引子   

　　2 Chen混沌系统的镇定控制

　　根据Chen混沌系统的状态方程，设计控制器进行Chen混沌系统的镇定控制，状态变量渐进收敛到零。带有控制器的受控Chen混沌系统，表示为：

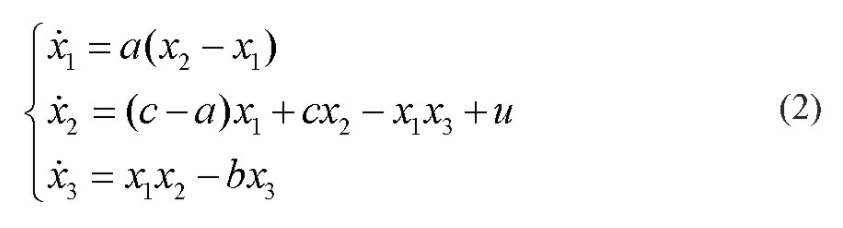
　　其中，u为设计的控制器，x1,x2和x3为状态变量。

　　对于Chen混沌系统，当状态变量x2=0时，由式（2）的第1个和第3个微分方程可以得到下面的子系统：

　　对于式（3），由于a>0且b>0,状态变量x1和x3渐进收敛到零。为了使状态变量x2收敛到零，设计控制器为：

　　其中，k1为自适应参数，且k1<0.参数k1的更新率为：

　　其中，k 2为常数，且k 2<0.

　　采用ode45函数进行系统的数值仿真，Chen混沌系统的初始状态设定为x1（0）=2,x2（0）=-4,x3（0）=15,步长为0.001秒，仿真时间为5秒。在控制器中，参数的初始值为k1（0）=-3,参数设定为k 2=-2.采用MatLab语言进行仿真实验，脚本程序为：

　　仿真实验运行后，状态变量的响应曲线如图2所示，状态变量渐进收敛到零，能够实现Chen混沌的镇定控制。参数的响应曲线如图3所示，控制器的响应曲线如图4所示，控制器最终收敛到零。

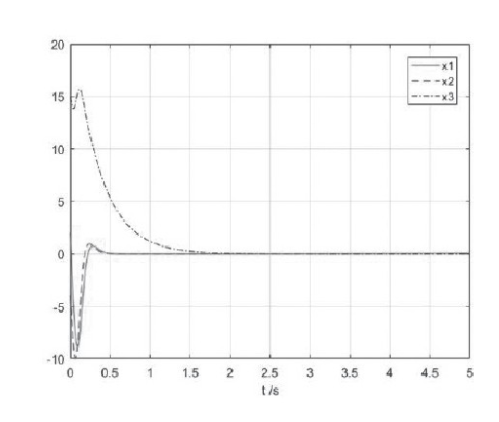
　　图2 状态变量x1,x2,x3的响应曲线   

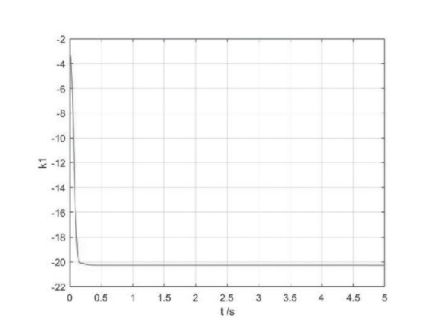
　　图3 镇定控制时k1的响应曲线 

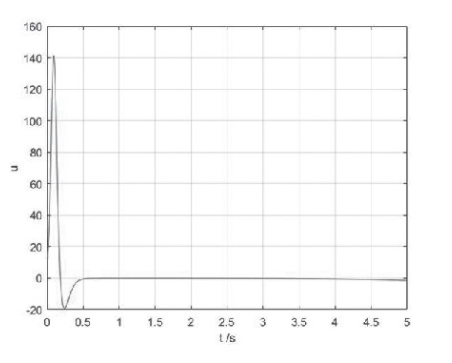
　　图4 镇定控制时控制器u的=响k1 x应2曲线   

　　3 Chen混沌系统的同步控制

　　驱动系统和响应系统均为Chen混沌系统，通过驱动系统和响应系统建立同步误差系统，设计控制器进行Chen混沌的同步控制，同步误差渐进收敛到零。以式（1）的Chen混沌系统为驱动系统，响应系统表示为：

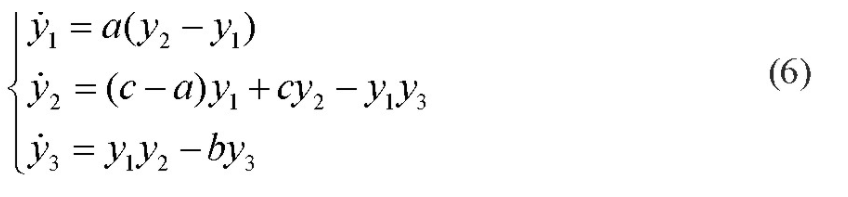
　　其中，y1,y 2和y3为响应系统的状态变量。驱动系统和响应系统的同步误差分别为e=1 y1-x1,e=2 y 2-x2,e=3 y3-x3.根据式（1）和式（6）得到受控同步误差系统为：

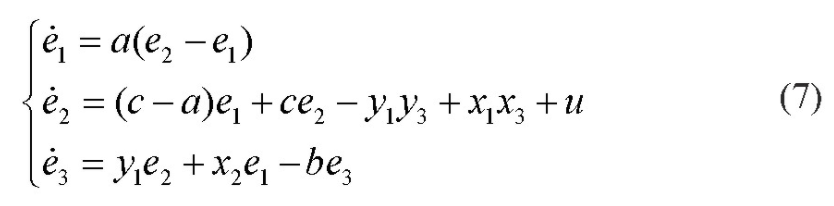
　　其中，u为设计的控制器。同=?步e（5）1误a差（e2为-零e1）时，式？（7）中的第1个和第3个微分方程变？为e（5）2:=（c-a）e1+ce2-y1

　　由于a>0且b>0,同步误差e=1和ey=31渐-进xy13收-x敛3到零。同理，可以设计控制器为：

　　其中，k1为自适应参数，且k1<0.参数的更新率为：

　　其中，k 2为常数，且k 2<0.

　　在数值仿真实验中，驱动系统的初始状态设定为，响应系统的初始状态为y,则同步误差的初始状态为。采用ode45函数进行数值仿真，步长为a.001秒，仿真时间为4秒。在控制器中，参数ke的始值为，参数设定为。仿真实验运行后，同步误差的响应曲线如图5所示，同步误差渐进收敛到零，能够实现驱动系统和响应系统的同步控制。在同步控制中参数k1的响应曲线如图6所示。同步控制中控制器的响应曲线如图7所示，控制器最终收敛到零。仿真结果表明，设计的控制器能够进行Chen混沌系统的同步控制，同步误差快速收敛到零。

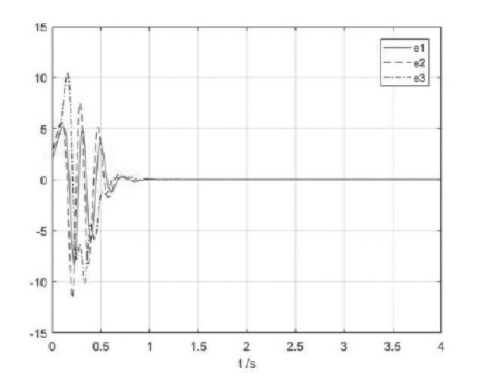
　　图5 同步误差的响应曲线  

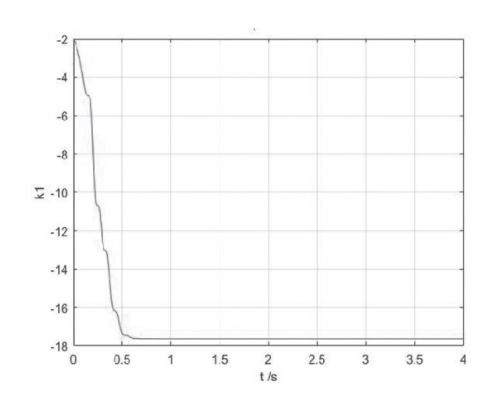
　　图6 同步控制时参数k1的响应曲线

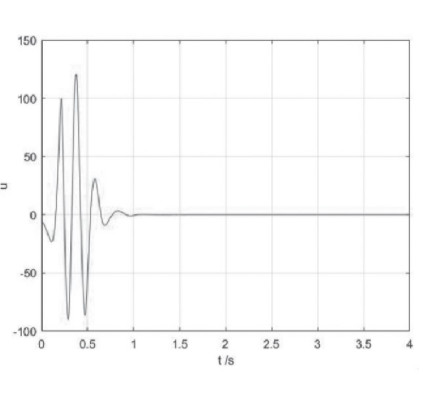
　　图7 同步控制时控制器u的响应曲线   

　　4 结论

　　根据Chen混沌系统的状态方程，只采用一个控制器进行Chen混沌系统的镇定控制，状态变量渐进收敛到零。根据同步误差系统，只采用一个控制器进行Chen混沌系统的同步控制，同步误差渐进收敛到零。采用四阶-五阶龙格库塔方法进行系统的数值仿真，并对仿真结果进行分析。本文设计的控制器较简单、易实现，能够实现Chen混沌系统的镇定控制和同步控制。

　　参考文献

　　[1]任涛，井元伟，姜囡。混沌同步控制方法及在保密通信中的应用[M].北京：机械工业出版社，2015.

　　[2] 孙克辉。混沌保密通信原理与技术[M].北京：清华大学出版社，2015.

　　[3]Chen G,Ueta T.Yet another chaotic attractor[J].International Journal of Bifurcation and Chaos,1999（9）：1465-1466.

　　[4]ZHONG G Q,TANG W S.Circuitry implementation and synchronization of Chen's attractor[J].International Journal of Bifurcation and Chaos,2002,12（6）：1423-1427.

　　[5]张国山，牛弘。一个基于Chen系统的新混沌系统的分析与同步[J].物理学报，2012（11）：137-147.

　　[6]胡春华，王春梅。基于Chen系统的自动切换混沌系统的设计与同步[J].扬州大学学报（自然科学版），2015,18（4）：57-62.

　　[7]李德奎，连玉平。单参数Chen系统的动力学分析及电路实现[J].自动化与仪器仪表，2014（3）：93-95.