
一、引言
作为现代金融理论的三大基石之一,资本资产定价模型(CAPM 模型)有着极为广泛的应用。自提出以来,国外一些学者就一直广泛利用此模型对股票市场进行有效性检验,得出的结论基本上都是支持 CAPM 模型的,即股票的收益和风险呈正相关的线性关系。20 世纪 90 年代以来,随着我国证券交易市场的蓬勃发展,越来越多的中国学者开始利用 CAPM 模型对国内股票市场进行实证研究。本文选取深圳股票交易市场中 2014 年 5 月 28 日至 5月 30 日和 2014 年 6 月 3 日至 6 月 6 日这 7 天的 100 支股票数据,利用 CAPM 模型对其进行时间序列回归和横截面回归,以探讨 CAPM 模型对中国股票市场检测的有效性。
二、CAPM 模型概述
1、CAPM 模型的基本前提假设
CAPM 模型是以现代资产组合理论和有效市场假说理论为基础的,其前提假设有:一是市场上的投资人都是风险厌恶者,他们根据均值方差规律作出投资决策,力求规避风险并获得最大回报。二是市场是有效的,其信息是完全对称的。投资者所拥有的信息是通畅的,且其他投资者有类似的分析方法、对未来市场有相同的预期。三是资本市场是一个完全竞争市场,所有的投资者都是资产价格的接受者,单个投资者的买卖行为不会对资产的价格产生影响。四是市场中存在无风险资产,所有投资者可以用一个固定的无风险利率自由借贷这些资本。五是所有投资者都处在同一个投资周期。六是资本市场是无摩擦的,不存在卖空限制,不存在个人所得税以及交易费等额外成本。七是每种证券的收益率均服从正态分布,每项资产都是无限可分的。
2、CAPM 模型形式
CAPM 模型以“资本市场线”和“证券市场线”为基础,前者揭示了经过投资多样化处理的有效投资组合收益率与其总风险(标准差)之间的关系;后者则将某项特定证券的期望收益率表示成其系统风险的线性函数。CPAM 模型不仅给出了均衡市场中风险资产的定价关系,还提供了一种潜在投资项目估计其必要收益率的方法。其形式如下:E(ri)=rf+βi[E(rm)-rf].其中,E(ri)表示第 i 种股票的期望收益率,rf表示所借贷的无风险收益利率,E(rm)表示证券市场组合的期望收益率,βi表示第 i 种股票的系统风险值,所表示的是某一段投资组合的风险程度与市场证券组合的风险程度的比值,即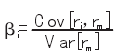
3、CAPM 模型的意义
资本资产定价理论认为,一项投资所要求的必要报酬率取决于以下三个因素:无风险报酬率、市场平均报酬率和投资组合的系统风险系数即 β 系数。CAPM 模型说明了单个证券投资组合的期望收益率与相对风险程度间的关系,即任何资产的期望报酬一定等于无风险利率加上一个风险调整。后者相对于整个市场组合的风险程度越高,需要得到的额外补偿也就越高,这也是 CAPM 模型的主要意义。
4、CAPM 模型的作用
CAPM 模型的具体作用有以下两方面:一是有助于资产分类,优化资源配置。对于模型中的风险因子 β,可以通过它的大小来对股票进行分类:当 β>1 时,称这类股票为进攻型股票(股票的风险要比市场组合平均风险大一些,相对地就要求有较高的回报);当 β=1 时,称这类股票为中性股票;当 β<1 时,称这类股票为防御性股票。在此基础上,投资者就可以根据其对收益和风险的不同要求,进行投资组合管理,从而使投资更为合理。二是为资产定价、为投资者的投资行为作出有效的指导。虽然 CAPM 模型的成立要求有很多的假设前提,但投资者依然可以根据市场证券组合收益率的估计值和证券的风险因子 β 的估计值去计算证券在市场均衡状态下的期望收益率,根据所得的结果和自身的喜好决定投资什么样的股票。
三、CAPM 在深圳股市的实证检验
1、数据的选取
选取 2014 年 5 月 28 日至 5 月 30 日和 2014 年 6 月 3日至 6 月 6 日,一共 7 天的股票每日收盘价数据,并从中随机选取深圳股票市场 100 只股票为研究对象,这 100 只股票分别属于不同的行业,可以避免数据的单一性,从而能够充分地反映整体股市的性质。
2、模型的选择
模型的基本公式是 rit-rf=α+βi(rmt-rf)+uit.其中 rit-rf表示在 t 时间时第 i 种证券资产的风险溢价,rf表示无风险收益率,rmt表示证券市场组合的期望收益率,βi表示第 i种证券的系统风险值。
3、指数的计算
(1)无风险利率的计算。选取 2014 年一年期居民定期存款利率作为无风险利率,折算成日利率,即 rf=0.0625%.
(2)收益率的计算。采用对数法,设 (tt=1,2,3,4,5,6,7)为时间,价格为 Pt,i 为某支股票,m 为证券组合,则 rit=lnpt-lnpt-1,rmt=lnpmt-lnpmt-1.
四、数据的处理
1、时间序列回归
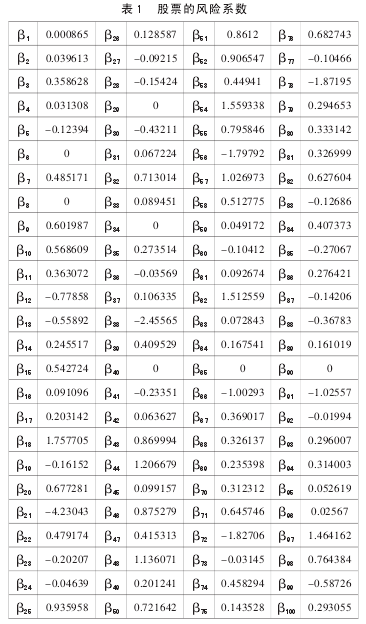
固定股票 i,求 i 在不同时期(t=1,2,3,4,5,6,7)的收益率 rit、rmt,用 rit对 rmt直接进行回归,估计出每支股票的风险系数(i=1,2,…100),具体数据如表 1 所示。
2、横截面数据回归固定时间 t,同时选取 2014 年一年期居民定期存款利率收益率作为无风险利率,即 rf=0.0625%,设 y 为每支股票的收益率减去无风险收益率的值,用 y 对 β 系数回归,得到 7 天的常数项系数分别为 α1:0.0060817、α2:-0.009995;α3:-7.17E-05;α4:-0.003516;α5:-0.013376;α6:0.0099559;α7:-0.014855.
五、数据解释
对于回归系数 βi,它代表了股票相对于市场的系统风险,这类风险不能通过投资多元化来消除。根据此值,投资者可以根据自己的喜好去选择投资。追求高回报的投资者,则可选择 β 估计值大一些的股票;相反,对于那些不愿意承担高风险或无力承担高风险的投资者,则可以选择 β估计值较小的股票。根据表 1 的结果,100 支股票中 β 估计值大于 1 的只有深华发 A、德赛电池、深赛格、北方国际、华侨城 A、天健集团、徐工机械这 7 只支股票,这些属于进攻型股票,其余的股票都属于防御型股票。
从得出的 α 值可以看出,在这 7 天中,常数项 α 都不等于 0:α>0 时投资股票是有效的,故该股票需求会增加,使之即时价上涨;α<0 时则相反。同时,需要注意的是,在这 7 天中,市场既受到节假日对于股票市场的影响,又受到 2014 年 6 月 10 日发行的第三期、第四期高利率国债的影响。在信息不对称情况下,一部分投资者抽取资金转投国债,一部分投资者盲目投资,这也影响着投资人的选择。
六、结论
综上看来,CAPM 模型还不完全适合我国的股票市场。这是由多种因素共同影响的。比如,我国的股票市场起步发展晚,比起西方发达国家股票市场仍不够成熟,不能满足市场有效假说。再比如,目前并非所有投资者都是理性的,大多数投资者都会或多或少受到虚假信息的影响。
CAPM 模型作为现代金融投资的核心理论,为我国投资业的发展作出了重要贡献。它的一系列严格的假设前提使得即使是较为成熟的证券市场也不可能严格满足,但它对证券市场及广大的投资者仍具有极大的指导意义,因为它不仅给出了风险资产的定价关系,还为投资者提供了一种对潜在投资项目估计其必要收益率的方法。因此,我们需要不断改进 CAPM 模型,使之不断完善,同时伴随着我国证券市场的不断发展、不断成熟,要让其更好地为投资者所运用。
【参考文献】
[1] 郑晓亚、肖莹:股权风险溢价理论研究综述---以 C-CAPM模型为主线[J].贵州财经大学学报,2013(6)。
[2] 阮涛、林少宫:CAPM 模型对上海股票市场的检验[J].数理统计与管理,2010(7)。
[3] 王飞、侯为波:CAPM 模型在上海股市的实证检验[J].淮北师范大学学报(自然科学版),2012(2)。
[4] 李红霞、邸鸿喜、李琰等:CAPM 模型在中国股票市场中的有效性检验[J].统计与决策,2014(7)。
一、引言改革开放以来,进入中国的外商直接投资(以下简称FDI)快速增长,2012年,中国实际利用FDI达到1117亿美元,与1992年的110亿美元相比,增长了9.15倍。FDI大量流入中国,对缓解内资短缺、推动技术创新和经济增长等起到了十分重要的作...
对风险资本分阶段投资的研究包括理论研究和实证研究。在分阶段投资理论研究方面,从研究视角进行分类,可以分为基于外生视角的研究和基于内生视角的研究。对外生性问题的研究,主要集中在分阶段投资契约的订立和阶段性金融工具的选择上。先不论证分阶段投...
一、引言风险投资(以下简称风投)是推动科技创业和创新的关键金融力量。近年,中国风投行业有明显增长,但存在两个突出问题:一是风投公司内部管理水平不足,投资效果不理想;二是地方政府成立的风险投资引导基金缺乏有效的操作模式。①发展风险投...
本文研究了实际利率和通货膨胀率波动对美国黄金价格的影响。通过对测试结果的分析, 证明了黄金价格与实际利率和美元指数之间存在显着的负相关关系。然而, 在通货膨胀率和黄金价格之间并没有显着的线性关系。只有在恶性通货膨胀的情况下, 黄金才能起到抑制通货...