股票投资是投资者通过购买股票以获得一定预期收益的投资。企业是股票投资的基础,股票投资的收益最终来源于企业的净收益,如果没有企业的净收益作为支撑,股票投资收益只能是空中楼阁,是一种泡沫收益,而投资者进行股票投资也是企业获取资金的一种手段和方...
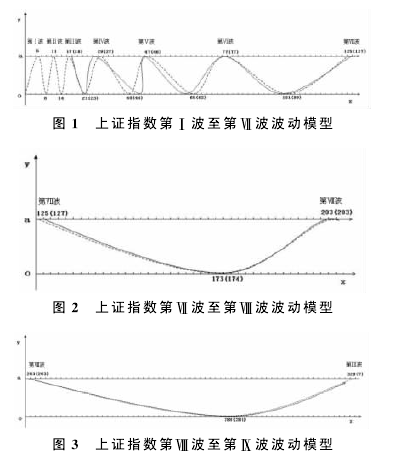
暴跌之后往往盈利机会较多……中小投资者在股票市场中有无数次亏损的惨痛经历与深刻教训。因此研究上证A股指数与个股之间涨跌幅关系与其中的概率问题有一定的现实意义,为中小投资者提供一种合适的概率投资策略。...
经过两地多年的论证、商谈,沪港通于2014年取得了重大进展。随着两地证券交易所在2014年9月4日正式签署《四方协议》,沪港通已全面驶入快车道,为项目最后顺利实施奠定了坚实的基...
一、引言工业革命以来,人类社会发生了翻天覆地的变化,人们在创造出大量物质财富的同时,也导致了一个重大的环境问题----全球气候变暖。研究表明,导致气候变暖的罪魁祸首是人们在经济活动中大量排放的温室气体----二氧化碳。因此,要从根本上解决气候变化...
股神巴菲特说过,要想获得高投资回报,一定要学会读财报。股票投资离不开财务分析,作为外部投资者能够获取的重要财务分析信息就是公司定期、不定期发布的财务报告。财务报告的组成主要包括:资产负债表、利润表、现金流量表、所有者权益变动表,以及会计报...
随着现代经济的高速发展,股票投资是一种获得资金的众多途径中之一,但是在投资的同时,也存在着一定的风险。所以,在股票投资方面,要对其投资做出分析。同时,也要对一些股票知识有一定的了解,在股票投资方面,尽可能地把它当作是一种娱乐或者挣钱的途径...
浙江苏泊尔股份有限公司是一家主要从事厨房炊具和厨卫小家电、大家电、健康家电的研发、制造和销售的企业,是国内炊具行业第一家上市的企业和省级高新技术企业(股票代码002032)。...
十八届三中全会指出,要健全多层次资本市场体系,推进股票发行注册制改革使证券发行制度改革再次成为国内证券市场研究领域的热门话题。事实上,中国股票发行制度由核准制向注册制改革已成为一种历史必然趋势,未来注册制改革将成为中国新兴+转轨发展期,资本...
股票发行制度是整个股票市场制度建设中最基础的环节之一,其作用机理是通过制度的激励与约束,明确发行市场主体间的责权关系,强化竞争机制,对资本有效配置和保护投资者利益有重要影响。不断推进发行制度的市场化改革,既是深化我国经济体制改革的必然要求...
天下熙熙皆为利来,天下攘攘皆为利往。因为利润获取看似便捷,炒股成为了中国十大经济热词。而在这场没有硝烟的战争中,利润就像鬼,大多数散户只听过没摸过,不说只听过没见过是因为散户大都有过浮盈,只是没有落袋为安。下半年随着股市不断突破各种均线,...