5. 模型的建立。选择 TARCH( 1,1) 模型,得到均值方程为式( 5) :
rt= 0. 081051rt - 1+ 0. 000489 + μt( 5)。
方差方程为式( 6) :
δt2= 6. 97* 10- 6+ 0. 035483* μ2t - 1- 0. 025692* μ2t - 1It - 1+ 0. 957780* δ2t - 1( 6)。
预测的区间为 2014 年 7 月 1 日 ~2015 年 5 月 22 日。根据模型首先模拟样本收益率,得到 985 个样本残差,然后对样本进行排序,根据置信度找到相应的残差,再对 2014 年 7 月 1 日的收益率进行预测,两者相加得到 VaR.在对 2014 年 7 月 2 日进行计算时,残差序列去掉第一个残差,加入 2014 年 7 月 1 日的残差,再对残差序列排序,根据置信度找到相应残差值,并与 7 月 2 日的预计收益率相加得到 VaR.以此类推,得到 2014 年 7 月 1 日 ~2015 年 5 月 22 日的 VaR 值。
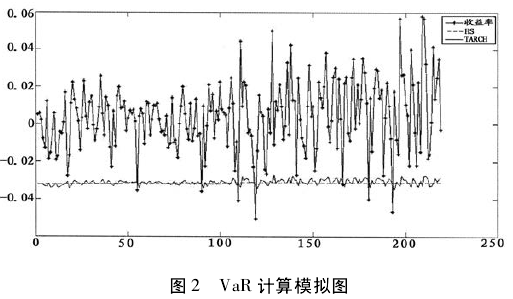
同样,若模型为 ARMA( 1,1) ,也可得到 2014 年 7 月 1 日 ~2015 年 5 月 22 日共 219 个 VaR 值。图 2为在 0. 95 的置信度水平下,从 2014 年 7 月 1 日 ~2015 年 5 月 22 日的实际收益率,HS 方法、HS_NEW( 以TARCH( 1,1) 模型为例) 计算的 VaR 值的比较。
在图 2 中,最上面的线是收益率曲线,而下面的两条曲线分别是用 HS 方法和 TARCH 方法来计算的VaR 曲线。其中较平缓的是 HS 方法计算的 VaR 曲线,波动较大、较为灵活的曲线是用 TARCH 方法计算得来的。
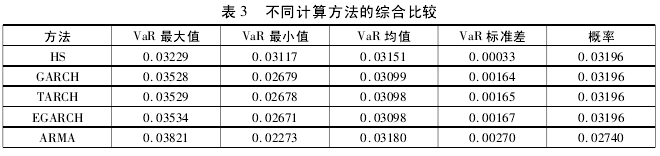
表 3 为各种模型的 VaR 计算情况,将 VaR 作为给定置信水平下的损失最大值,所以 VaR 值取正数。
表 3 列示了用不同方法计算的从 2014 年 7 月 1 日 ~2015 年 5 月 22 日的 VaR 的最大值、最小值、均值、标准差和概率。其中概率是指当天收益率的损失值大于计算的 VaR 值的天数占所有比较天数的比率,即损失超过计算的 VaR 值的天数除以总天数。
五、结论。
本文将 GARCH 类模型与历史模拟法相结合,提出了一种改进的历史模拟法来计算风险价值。从VaR 最大值和最小值可以看出,HS_NEW 方法较传统的 HS 方法对风险的预测更加灵活。在 HS_NEW 方法中,ARMA 模型与 GARCH 类模型相比,ARMA 模型计算的 VaR 最大值最大,VaR 最小值也最小,所以在预测方面更加灵活。在预测的效果上,ARMA 模型较另两个模型更加准确。但是从 VaR 的均值上看,AR-MA 模型的均值最大,这也意味着 ARMA 模型在某种程度上高估了风险。而 GARCH 类模型在出错方面比 ARMA( 1,1) 更加接近 5%,与 HS 方法出错次数一样,但是,GARCH 类模型的均值最小,说明 GARCH类模型对风险的计算更加精确。总的来说,相比 HS 方法,HS_NEW 方法在计算风险时既保留了 HS 和HSAF 的优点,而且能更加灵活、精确地计算 VaR,可为投资者在创业板投资时提供一种新的、准确性更高的计算风险的方法。
[参考文献]
[1]Hulll C. J. ,White D. A. Value at Risk When Daily Changes in Market Variables Are Not Normally Distributed[J]. TheJournal of Derivatives,1998,5( 3) : 9 - 19.
[2]叶青。 基于 GARCH 和半参数法的 VaR 模型及其在中国股市风险分析中的应用研究[J]. 统计研究,2000,( 12) : 25- 29.
[3]Hendricks D. . Evaluation of Value at Risk Models Using Historical Data[J]. Economic Policy Review,1996,4: 39 -69.
[4]Cabedo J. D. ,Moya I. Estimating Oil Price Value at Risk' Using the Historical Simulation Approach[J]. Energy Econom-ics,2003,25: 239 - 253.