本文选择内蒙古2005年1月至2012年12月最新的月度CPI数据作为研究对象,构建ARIMA(p,d,q)模型,在模型拟合效果优良的基础上,预测CPI的未来趋势,为政府决策部门有效实施物价调控政策提供数量依据。
一、ARIMA预测模型的建模思想
时间序列预测是通过历史数据来分析目标对象随着时间而改变的内在规律,然后利用外推机制将这种规律推演到未来。时间序列是随着时间t而随机变化的变量,该时序的单个构成序列值虽然不确定,但是整个序列却呈现一定的变化规律,可以用数学模型去近似地描述。现实社会中,人们常运用时间序列ARIMA模型来进行实证研究,以达到最小方差意义下的最优预测效果。

二、数据资料
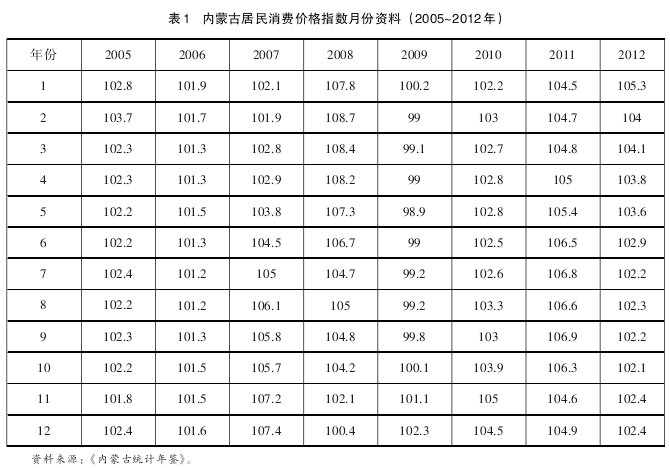
以内蒙古2005年1月到2012年12月最新月度CPI(上年同期为100) 资料为研究对象,数据如表1所示。
(一)分析内蒙古CPI数据时间序列表
从表1的月度CPI时序变化情况来看,价格指数随着时间的推移具有明显的波动变化趋势,初步判断是一个非平稳的时间序列。为进一步判断该时间序列的平稳性,使用ADF检验方法对数据进行单位根检验,如表2。
ADF检验值为-2.183056,明显大于5%和10%检验水平下的临界值,所以认为这个序列为显着非平稳序列。
(二)一阶差分CPI数据的ADF平稳性检验
绘制一阶差分后的数据时间序列图,其基本上达到平稳,可以认为该序列为纯随机序列,再通过对原数据一阶差分序列进行ADF检验,结果显示,ADF统计量为-3.236321,小于5%和10%检验水平下的临界值-2.8928与-2.5833,从而可知一阶差分序列在5%水平下为平稳序列。
三、实证分析最优模型的判定
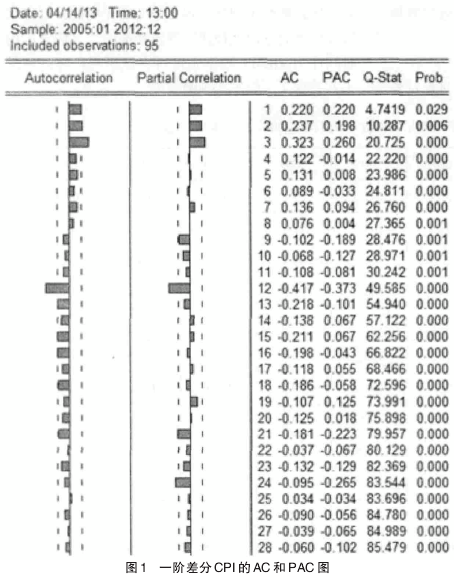
通过上述分析,我们采用ARMA(p,d,q)模型,其中d=1,p是自回归的阶数,q是移动平均的阶数,通过对CPI一阶差分序列的自相关和偏自相关图(如图1)的观察可以看出,偏自相关系数在滞后阶数为3、12和24时显着不为零,可以分别取p=3、p=12、p=24,自相关系数在滞后阶数为3和12时显着不为零,可以分别取q=3、q=12。
为提高模型的精确度,减少主观性的影响,我们建立多个模型,利用AIC准则对模型进行评判比较确定最优模型,最终确定最优模型为ARIMA(24,12)模型。
模型数据表达式如下:
DX=-0.011745-0.637024-0.027758dxt-24-0.308895-0.885797ut-12-5131.924+ut
四、模型的诊断检验
ARIMA模型构建完成以后,判断其是否合适,首先应当检验残差序列是否为白噪声。当残差序列不是白噪声时,说明还有信息包含在残差中,所建立的模型肯定不是最终模型,其他参数也不能完全代表,还需要进一步拟合模型。当残差序列属于标准的白噪声时,则P值的概率应该大于0.05,因此可以对其进行回归拟合,将实际值和拟合值之间的残差进行检验。
五、残差白噪声检验
残差序列的P大于0.05不够明显,P值不显着,所以残差不是白噪声序列,说明还有信息包含在残差序列中,模型还需要进一步拟合。根据自相关和偏自相关的特点,进行模型定阶,自相关图中只有延迟3阶和12阶的自相关系数显着大于2倍的标准差,所以考虑构造疏系数模型ARIMA(p,d,(q1,q2)),建立多个模型进行尝试,同时利用AIC准则对模型进行比较,最终确定最优模型为ARIMA(3,(3,12))模型。
模型数据表达式如下:
DX=0.0182220.889775+0.387910dxt-34.560067-0.176191ut-3-34.6093-0.724719ut-12(-9.294006)+ut
再次进行残差白噪声检验,检验统计量的P值都显着大于显着性水平0.05,可以认为该残差序列即为白噪声序列,说明ARIMA(3,1,(3,12))模型对该序列建模成功,所以选取的模型能较好地用于进一步的分析和预测。
六、模型的预测和分析
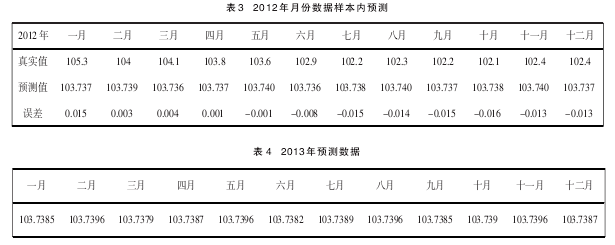
利用Eviews软件,选取2012年1月到12月数据进行样本内预测,如表3。
其预测误差的绝对值均小于0.016,由此我们可以知道预测的精度相对较高,说明我们的模型具有较强的解释显示的能力,所以可以利用已经验证完毕的模型来预测该事件序列的未来趋势,预测数据如表4。
从表4中可以看出2013年的CPI走向有上升的趋势,说明内蒙古的物价水平还需要一定的调控,有关部门应该采取一定的措施。
该模型只考虑了时间序列本身的特性,而没有考虑其他一些不确定因素对消费者价格指数的影响,因此这些因素在ARIMA模型中是以随机误差项来反映。该模型仅适合短期预测。
七、结论
本文以内蒙古2005年1月至2012年12月最新的月度CPI(上年同期=100) 作为研究对象,通过成熟的时间序列建模技术,构建了该样本期间ARIMA(3,1,(3,12))的最优模型。经过残差检验,模型拟合较好,统计量的P值显着,精度较高,可见模型的效果很好。因此通过对居民消费价格指数应用时间序列的相关分析技术构建模型,可以很好地模拟和预测价格指数今后一段时间CPI的变化规律,对数据的预报有一定的参考价值。从模型的动态预测结果来看,2013年内蒙古的物价形势还是需要一定的调控。因此应加强对物价的控制,采取相应有效措施,将物价变动的幅度严格控制在可控范围之内。
参考文献
[1] 王燕.应用时间序列分析[M].北京:中国人民大学出版社,2005.
[2] 内蒙古自治区统计局.内蒙古统计年鉴2011[M].北京:中国统计出版社.
[3] 齐丽. 甘肃省居民消费价格指数统计分析[D].兰州商学院硕士论文,2011.
[4] 朱威,钟惟剑. ARMA模型在居民消费价格指数预测中的应用[J]. 金融经济,2008,(16) .